现代模态逻辑的形式分析初步——魔态羽翼的跨世界逃逸与“刑师”分析下的在劫难逃

万小龙

(华中科技大学 哲学系， 湖北 武汉 430074)

【逻辑学】

现代模态逻辑的形式分析初步
——魔态羽翼的跨世界逃逸与“刑师”分析下的在劫难逃

万小龙

(华中科技大学 哲学系， 湖北 武汉 430074)

现代模态逻辑其实是按一阶逻辑公理和规则对经典真值函数做分类研究。模态命题逻辑中任一个可能世界集W仅表示与某一公理模式相应的一组二真值函数，相应的可能世界间的关系R就是这组真值函数共有的一种集合性质。任一公理模式在一框架内有效，就是将属于W的每个真值函数式按K-2分别依次代入该公理模式中的每一个“□”，使得形成一组经典定理。

二分性；非真值函数；经典二变元真值函数；模态公理模式；K-1；K-2

逻辑的本性(the nature of logic)是二分性，并通过不断的形式化二分将繁杂的经验、超验或先验的东西(抽象的哲学和艺术、形象的文学及生活、高深的数学物理等科学理论、超越的上帝或大千世界等，乃至各种逻辑理论自身)明晰和简化，并保持严密和可靠。任何集合P都可以二分为其子集p和非p。可以二分与不可以二分也仍是一种二分。

一、非真值函数的二分

无论y是否为x的函数，它至少总是与负y互为函数。这就是说任何被称为非函数的东西至少是另一东西的函数。所谓“非真值函数”就是非真值的非函数、非真值的函数或真值的非函数。真值的非函数又可分为非二的真值的和二真值的非函数。本文仅讨论二真值的非函数，即先把非真值函数二分为并非二真值的非函数的非真值函数和二真值的非函数，又把后者分为非一元的和一元的，再把后后者如下二分：

p的任一二真值一元非函数Hp，或者等值或者不等值于下表的16个真值函数中的一个。

表1 经典二元函数真值表D=d(p，q)

二、一元算符二真值非函数

任何人当然总是或者属于或者不属于认可笔者的上述观点的人。如果有人属于“既属于又不属于”的人，那么他们不过是与不属于“既属于又不属于”也即“或者属于或者不属于”的那些人构成新的层次的“或者属于或者不属于”。从逻辑形式的角度看，所谓的对象语言与元语言的关系就可解释为新层次是包括以旧层次作为肢命题的同一层次的复合命题。

本文仅研究二真值的模态命题。现代模态命题逻辑LP的语言好像是在经典二真值的命题逻辑语言基础上增加了并仅增加表示“必然”的“□”和对偶地表示“并非□并非”即“可能”的“◇”。但在笔者看来，“必然”、“实然”和“可能”这些“神马”都是浮云。

一元算符二真值非函数Hp虽然不是p的真值函数，但它本身也是与q和p一样仅是二真值的，因此总可以等值于某个二真值函数(所有的二真值函数穷尽了二真值的所有真值指派)，而任意二真值函数是或者包括或者不包括一个以p为一个变元的多变元的二真值函数。对于多于二元的联接词联接的二真值函数，总是可以还原为某些二元联接词联接的多变元的二真值函数。先看16个二变元的真值函数，显然其中一变元p的四个真值函数已经包括在内：D1、D6、D11和D16。并且D7、D8、D9和D10也可以看做是以p为一变元的特殊多变元二真值函数。所以说，Hp在这个阶段实际上总是等值于表1中16个真值函数之一。

有二元联接词相联接的256个三变元函数可以看做是第三变元的真值指派对前面16个真值函数形成的新的组合排列，因此这时与每一个三变元函数等值的一元算符二真值非函数就可以看做是前面16个二真值非函数之间的256种两两叠置。依次类推，二元联接词相联接的n变元函数(n是大于2的自然数)就是16个二真值非函数之间的n-1重叠置。这样，我们有初步结论：有且仅有16个一元算符二真值非函数Hp，它们分别等值于表1中16个真值函数。概括“二探”一文(参见文献[5])中的一元算符真值表及其孪生，可得本文的表2。

表2 狭义一元算符真值表(二真值非函数)

三、模态命题逻辑公理与系统的系统性分析

如果任一模态基本命题□p属于16个Hp的集合，那么只要将16个真值函数分别代人模态公理即可求得。以最简便又常用的T公理(□p→p)为例，很容易发现：

(1)T公理中的□p表示一组而非一个p的非真值函数；

(2)这一组p的非真值函数分别等值于真值函数D6、D12、D13和D16；

(3)进一步，由于公理具有的二真值特性(表示蕴涵为真或推理有效)，T公理中的□p(在不包括叠置一元算符时)表示的非真值函数只能等值于真值函数D6、D12、D13或D16。

(4)T公理实际上表示并仅表示一组经典命题逻辑的定理：

“二探”一文(参见文献[5])中已发现，多变元的一元算符和叠置算符的语义有一点需注意，现改述如下：对于任一对Hp和Hp’来说，当Hp=f(p，q)时，Hp’=f(p’，q’)而不是f(p’，q)。例如，当H4p是p∨q时，H4s是s∨t。特设性的f(p’，q)形式对应K-1，一般形式f(p’，q’)对应K-2。K-1与K-2中的“□”均仅考虑二变元真值函数式，已足够反映模态逻辑的基本性质。例如p∧q∧r也是T公理中的□p，其实是叠置算符所形成。为了简单明晰，下文先考虑不包括叠置算符形成的非真值函数。

模态命题逻辑LPK-2：在经典命题逻辑基础上增加并仅增加的符号“□”有且仅有明确的经典意义：“□”与任意变元p组合形成的□p表示以p为一个变元而形成的16个二变元真值函数集(如表1)的一个子集。最大子集就是这16个真值函数集，最小的子集对于这16个真值函数是空集。容易算出总共有有限数量个不同的子集。模态公理就是在经典命题逻辑语言外仅增添了“□”或它的对偶“◇”或它们的各种叠置的公理。由于公理的特性(永真)和其中任何一个命题串的“二真值性”，任何公理中的□p只能是至少等价于16个真值函数中的一个而不可能为“空”，所以不等价的模态公理的总数就是正好比上述子集的总数少一个。模态命题逻辑好像是一系列逻辑系统的总称并且有且仅有WM个不等价的系统。不过，仔细分析发现：当□p正好表示16个真值函数的集合时，这时的模态命题逻辑公理就是经典命题逻辑的公理，相应的模态系统就是经典命题逻辑系统。而当□p表示小于16个真值函数的集合时，这时的模态公理就是一组经典命题逻辑的定理，所以相应的模态系统仍是经典命题逻辑系统。总之，模态逻辑不过是经典逻辑的成语。

本文暂不考虑一阶谓词逻辑LP’和相应的模态谓词逻辑LP’，但笔者认为任何一阶谓词公式都可以用一个或一组经典命题逻辑公式等价地表示。

四、对一些运算结果的分析

(一)K-1形式下的模态句法还原。

□p=f(p，r)，□q=f(q，r))，□□p=f(f(p，r)，r)；

K：︱—□(p→q)→(□p→□q)；4(传递)：︱—□p→□□p；q(对称)：︱—p→□◇p，

O：︱—□(□p→p)，E(欧)：︱—◇p→□◇p,V：︱—□p；Tr：□p↔p

T(自反)：︱—□p→p；M：︱—□◇p→◇□p，D(持续)：︱—□p→◇p

第一步，考虑最基本的模态公理K，将16个经典二元联结词依次代入K中的每个“□”，很容易发现这时的K公理是分别对16个经典二元联结词都有效的。

第二步，K-1形式下，把16个经典二元联结词依次、分别代人其他典型的9个模态公理中的每个“□”，不难得到下面的16张完整真值表(因为篇幅，略)和总表表3。

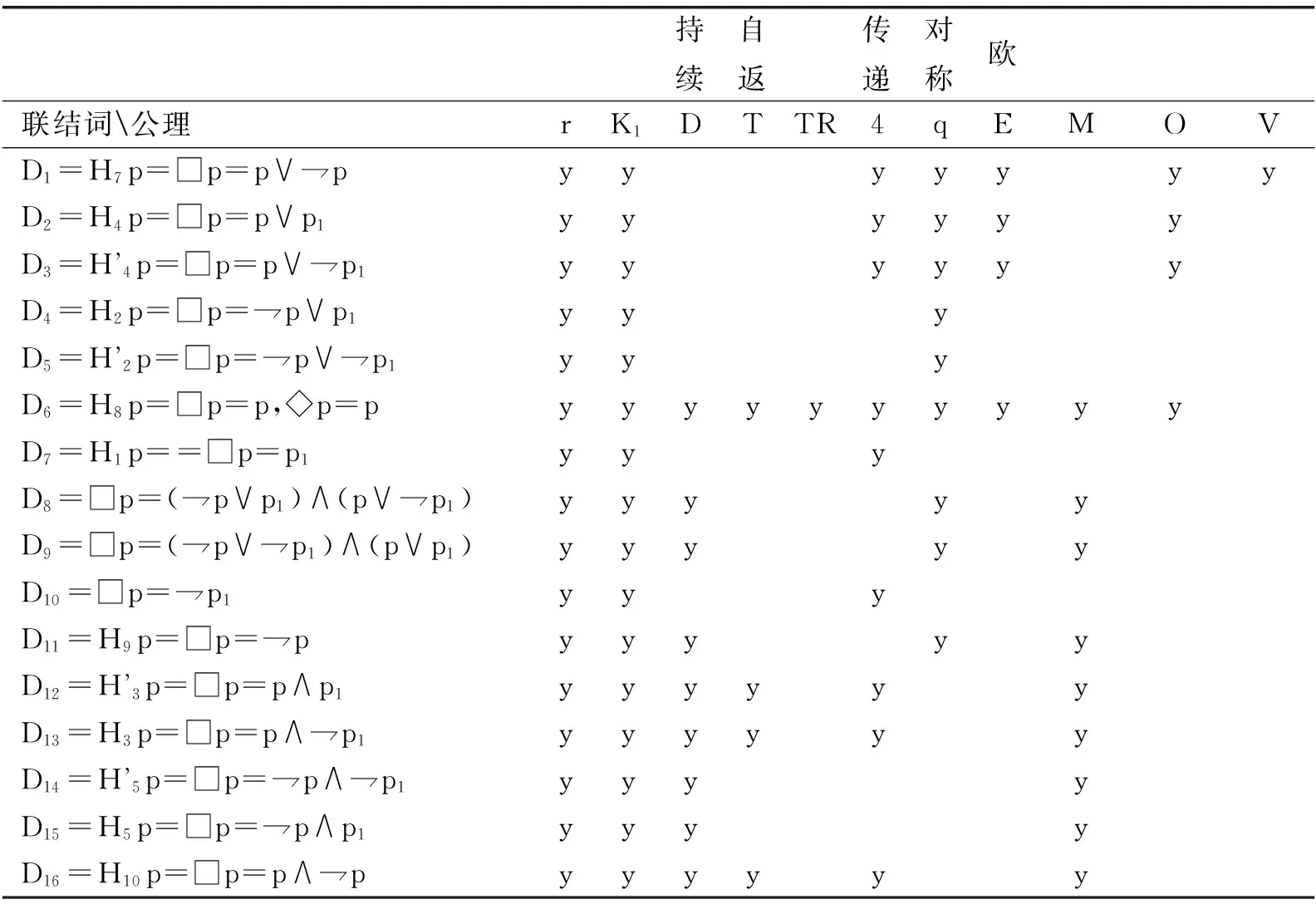
表3 10公理在K-1形式下公理模式有效性比较表(y表示有效)

表3中r公理就是经典公理，K公理是对16个经典二元联结词都有效的，但不难算出K-1情形下K系统中模态算子对于析取和合取都是等值分配的，这一点似乎不完全符合现代模态逻辑的经典结果(参见文献[1]第160-161页)。K-1的模态逻辑虽然仅是“瘦身”的而非真的模态逻辑，但由于它简单，能非常明晰地反映模态逻辑的最一般本性：模态算符“□”表示共有某种集合性质的一组经典真值函数式，模态公理表示一组经典定理，所有的模态命题系统都等价于经典命题逻辑系统。

(二)K-2形式下的模态句法还原。

K-2：□p=f(p，p1)，□q=f(q，p2))，□□p=f(f(p，p1)，p1’)。因为K-1是K-2的特设形式，而D、T、V和Tr是独立于K-1和K-2的，所以只要考虑表3中余下的6个公理中有效的那些项。施反证法(因为篇幅，略)于6个模态公理，不是很难就能 算出表4的结果。

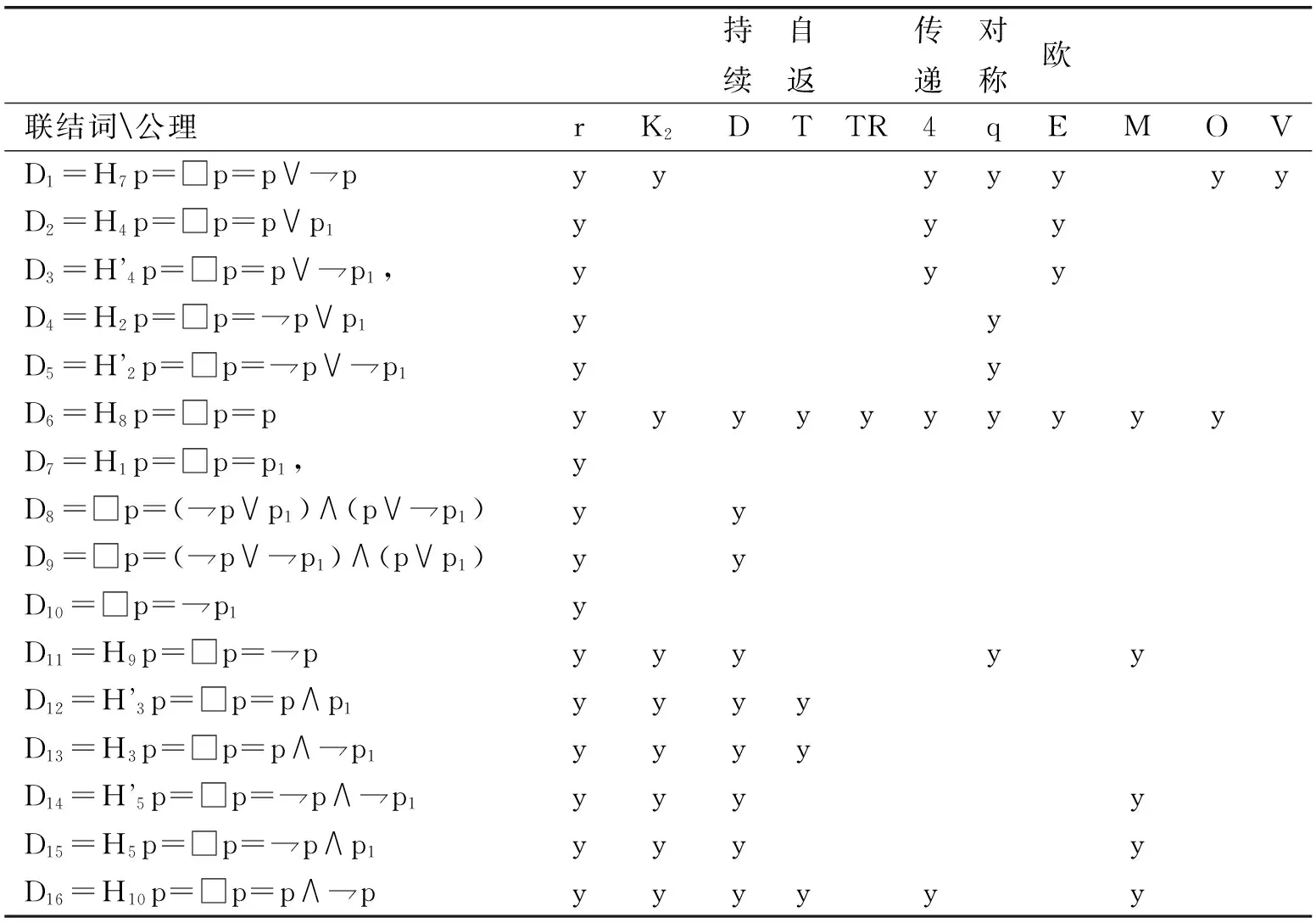
表4 10公理在K-2形式下公理模式有效性比较表(y表示有效)

对自然(或必然)化规则可以把N理解为把真值函数代入□p后的真值表的每一行都要符合“p为真时，□p为真”的条件。表4中的各个公理的结果加上N与现代模态逻辑经典文本中的模态系统中仅按句法推出的结果相比较，没有发现反例。不难发现，表4中各种公理的有效性之间的互推关系也符合现代模态逻辑的主要经典结果(参见文献[3]第126页)：

(1)自返性⟹持续性。

(2)对称性+传递性⟹欧性。

(3)(略)。

(4)自返性+欧性⟹对称性。

(5)对称性+欧性⟹传递性。

(6)对称性+传递性⟺对称性+欧性。

(7)对称性+传递性+持续性⟺自返性+欧性。

(8)自返性+对称性+传递性⟺自返性+欧性。

但显然K公理不是对16个真值函数均有效的，至少对H4即p∨q(的0010这行)无效。

五、对现有模态逻辑体系的解释

(一)虽然每个模态逻辑公理都不等价，但每个模态逻辑系统都是经典命题逻辑系统加一组经典命题逻辑中的定理，在基元意义上当然还是经典命题逻辑系统，所以都是等价的。因此说一个模态逻辑系统是另一个模态逻辑系统的扩充在上述意义上总是正确的。

(二)由于在不同模态系统中有不同的模态公理，因此导致不同的模态公理中“□”表示的“必然”的逻辑意义不相同，虽然这些不同的公理还原为经典定理的组合后，作为其组合成分的经典定理都是等价的。这里不仅反映了“非经典逻辑仅是经典逻辑成语”的逻辑基元特性，而且揭示了整体论的形而上学起源：不同的整体由相同基元集合的不同子集形成。

(三)每个模态公理反映其中的□p作为一组由p为一变元形成的真值函数对p的同一种集合性质。例如，LPK-2的T公理中□p表示且仅表示p、p∧q、p∧q和p∧p对p都具有自反的性质。说明可能世界语义学中“T公理中的那一组可能世界之间具有自反性”是一种近似正确但不够准确的表述(显然，p对p∧q并不具有自反性)。

(四)每个模态逻辑公理中的□p都表示了一组由p为一变元形成的数变元真值函数，这才是□p作为逻辑符号所反映的思维的形式意义。半形式化地可以把这一组真值函数(式)代表一集可能世界，或一堆臭皮囊，或一队具有魔法的羽翼，甚至孙悟空的一群变身。笔者根本就无需知道“□”作为“必然”的自然意义是如何抽象为逻辑形式意义的历史。

(五)LPK-2的必然化规则N存在才使得K-2形式下各种模态系统中各种公理与定理在真值语义中的可判定变得容易。但笔者根本就无需知道它究竟是谁让它反应何种集合性质。

(六)在可能世界语义学中，大部分模态逻辑公理都与一个一阶谓词公式对应，反之亦然。在笔者对模态逻辑的理解中，每一个模态逻辑公理都与一组命题逻辑定理对应，反之亦然。一方面说明仅从对模态逻辑做半自然半形式理解的可能世界语义学出发，很难找到或无法找到它们的一一对应；尤其当涉及像全通性这样的无特设性(即K-2形式的经典二真值语义)一阶公式时，就找不到对应的模态命题逻辑公式了。

(七)“K公理对所有模型均有效”的证明没有注意到K-2所反映的“模态算符的非完全可代入性”。f(p)如果表示p的一个真值函数，那么f(q)就表示q的同一个真值函数。但现在□p表示以p为一个变元形成的一个二变元的真值函数，那么□q表示的是与前一个二变元的真值函数仅有相同函数式的以q为一个变元形成的另一个二变元的真值函数。

(八)对模态命题逻辑的纯句法研究依照自然推理演绎的方法，其实它隐含着经典二真值语义，所以自然地使用了K-2形式，因此几乎没有错误结果。但因为不知一元算符的本性，，所以进展缓慢。

六、结论

按照二分性，可以先把可能世界集二分成现实世界(用p或A还是w表示现实世界其实没有区别)和并非现实世界：p和p，那么显然p∨p和p∧p也是可能世界；再在p中找到一个子集q，把可能世界集p再二分成p的q和p的q，等等。

现代模态逻辑是对经典真值函数做系统分类研究的经典逻辑。句法上，模态命题逻辑中任一公理模式的任一“□p”都表示使得这一公理模式有效的那一组以p为一变元形成的经典二真值函数，任一模态公理模式是且仅是一组经典命题逻辑定理。语义上，使用经典语义就已经充分，但由于d(p，q)不是p的严格意义上的函数，所以模态“□”具有非完全可代入性，即遵照K-2而非K-1的形式。可能世界语义学大致曲折地反映了这种句法和语义的统一：一个可能世界w就是(映射)一个经典二变元真值函数，一个世界集W就映射一组这样的真值函数，相应的可能世界间的关系R就是这组真值函数共有的一种集合性质，关系真值赋值论没有使用必要。W、R和K-2式经典赋值V构成一个框架。任一公理模式在一个框架内有效，就是将属于W的那一组真值函数式按K-2规则分别依次代入该公理模式中的每一个“□”，使得代入后形成一组经典命题逻辑定理或一个一阶谓词逻辑定理。

对许多现代逻辑系统是否为经典逻辑的认识过程，可借用唐代禅师青原惟信的话来说明：“老僧三十年前未参禅时，见山是山，见水是水。及至后来，亲见知识，有个入处：见山不是山，见水不是水。而今得个休歇处，依前见山只是山，见水只是水。”(《五灯会元》卷17)

[1] 杜国平.经典逻辑与非经典逻辑基础[M].北京：高等教育出版社，2006.

[2] 徐明.符号逻辑讲义[M].武汉：武汉大学出版社，2008.

[3] 李小五.模态逻辑讲义[M].广州：中山大学出版社，2006.

[4] 万小龙.经典命题逻辑联结词的泛函分析初探——一元算符是否可能穷尽[J].安徽大学学报：人文社会科学版，2011(6).

[5] 万小龙，李福勇，田雪.一元算符逻辑理论二探——义高一尺，道高一丈[J].安徽大学学报：人文社会科学版，2012(3).

责任编辑：王荣江

B815.1

A

1007-8444(2012)03-0322-05

2012-03-20

国家留学基金项目(200635015)；国家社科基金项目(2007ZXC49)。

万小龙(1964-)，教授，博士生导师，国家马克思主义工程“科学技术哲学”首席专家,主要从事科学哲学和逻辑学研究。