地下连续墙内埋管地热换热器传热模型
2012-10-30夏才初张国柱肖素光
夏才初,孙 猛,张国柱,肖素光
(1.同济大学 地下建筑与工程系,上海 200092;2.同济大学 岩土及地下工程教育部重点实验室,上海 200092)
在地下连续墙施工时,将热交换管绑扎在钢筋笼的主筋上而随钢筋笼下放至指定深度后再浇筑混凝土,可以将热交换管与地下连续墙结合在一起形成地下换热器(见图1).换热器内部循环介质不断流动便可以吸收地下连续墙及周围土体的浅层地温能,经热泵提升后供上部建筑冬季制热、夏季制冷,并全年提供热水[1].该技术的埋管施工与地下连续墙施工协同进行,额外工程费用少,又不需要额外占地面积,还省去室外机或冷却塔,且系统运行稳定,传热效果好,能解决在城市中推广地源热泵技术占地和初投资高的两个主要障碍,在人口密集的城市地区具有广阔的应用前景[1-2].20世纪90年代起,奥地利率先在维也纳地铁2号线车站的地下连续墙内埋管并投入使用[3],我国在建的新上海自然博物馆(上海科技分馆)也采用了该项技术.

图1 地下连续墙内埋管示意Fig.1 Schematic diagram of geothermal heat exchangers embedded in diaphragm walls
建立较为准确的地下连续墙内埋管传热模型是合理设计埋管换热器的前提,是降低工程造价的重要途径,也是推广该项技术的关键之一.由于地下连续墙的尺寸较大(宽度约0.8~1.0m),其热容不可忽略.建立传热模型时,需考虑地下连续墙和土体两种不同的介质,故地下连续墙内埋管与传统的垂直地埋管传热模型有较大的不同,桩埋管模型在此也并不适用.然而,地下连续墙内埋管技术是地源热泵技术的一个崭新的研究方向,国内外对其传热模型方面的研究并不多见.奥地利学者Brandl,Adam等对地下连续墙内埋管技术进行了现场测试和数值模拟工作,没有研究传热模型[3-5].曹诗定初步分析地下连续墙内埋管的传热模型,建议采用三个基本传热模型——平面热源、柱面热源和球面热源模型以分析传热[6],然而,实际的地下连续墙内埋管情况十分复杂,需要建立更准确的传热模型.
笔者首先根据地下连续墙内埋管的实际情况,建立开挖面以上和开挖面以下两部分的地下连续墙内埋管传热模型,然后采用格林函数法[7-16]推导其解析解,并给出了该模型在地下连续墙内埋管温度场分析和参数优化分析方面的应用实例.
1 传热模型
1.1 模型基本假定
根据地下连续墙内埋管的特点,建立传热模型时作如下假设:① 地下连续墙的外侧与土体紧密接触,无接触热阻;② 开挖面以上,地下室外墙内侧与空气直接接触,为对流边界条件,开挖面以下的地下连续墙内侧与土体紧密接触,无接触热阻;③ 假定两相邻热交换管之间的距离以及每组热交换管两支管之间的距离均相同;④ 忽略热交换管内流体流动产生的轴向对流传热,并假设每组U形热交换管进、回水支管的温度相同;⑤ 材料的热物理参数不随温度而变化;⑥ 由于热交换管的直径远小于地下连续墙的尺寸,为简化计算,将每个热交换管的支管假定为一个点热源;⑦ 假定地下连续墙无限长,可近似为无横向传热,计算单元之间为绝热边界条件,故可取一个计算单元来研究.
根据假定,开挖面以上的地下连续墙内埋管传热模型可取图2所示的计算模型.模型的地下连续墙左侧临空面为对流边界;右侧与土体紧密接触(忽略接触热阻);土体右边界取足够远,可认为右边界的土体温度不受热交换管运行的影响,假定为恒温边界.计算单元的上下边界假定为绝热边界.

图2 开挖面以上的地下连续墙内埋管传热模型Fig.2 Heat transfer model of heat exchangers embedded in diaphragm walls over excavation face
开挖面以下的地下连续墙内埋管传热模型可取图3所示的计算模型.开挖面以下的地下连续墙左右两侧均与土体紧密接触(忽略接触热阻);两侧土体的远边界取足够远,假定为恒温边界.计算模型的上下边界取为绝热边界.

图3 开挖面以下的地下连续墙内埋管传热模型Fig.3 Heat transfer model of heat exchangers embedded in diaphragm walls under excavation face
1.2 开挖面以上模型基本方程
基于能量守恒原理,可以得到开挖面以上的地下连续墙内埋管传热模型的传热微分方程及其边界条件

初始条件

边界条件
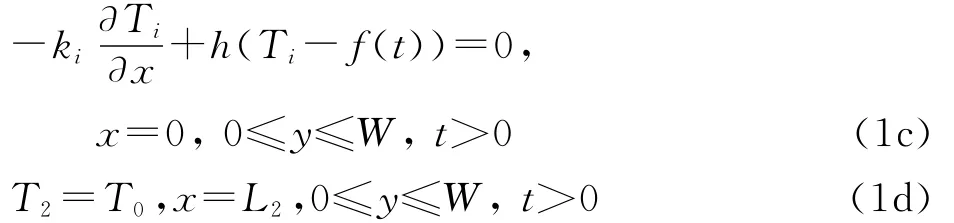

式中:T1,T2分别为地下连续墙、土体的温度,℃;k1,k2分别为地下连续墙、土体的导热系数,W·(m·K)-1;ql为热交换管支管每延米换热量,W·m-1;ρ1,ρ2分别为地下连续墙、土体的密度,kg·m-3;Cp1,Cp2分别为地下连续墙、土体的比热容,J·(kg·K)-1;h为地下连续墙临空面与空气之间的对流换热系数,W·(m2·K)-1;f(t)为气温,℃;T0为未扰动之前的原始地温,℃;t为时间,s;δ(x-a)δ(y-b)为狄拉克函数.
1.3 开挖面以下传热模型基本方程
基于能量守恒原理,可以得到图3所示传热模型的传热微分方程及其边界条件

初始条件
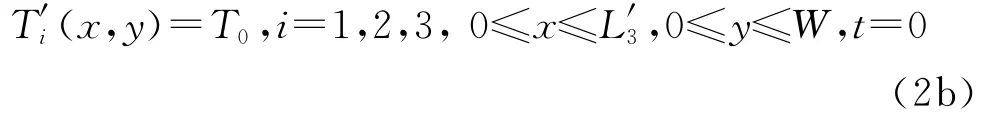
边界条件

连续条件
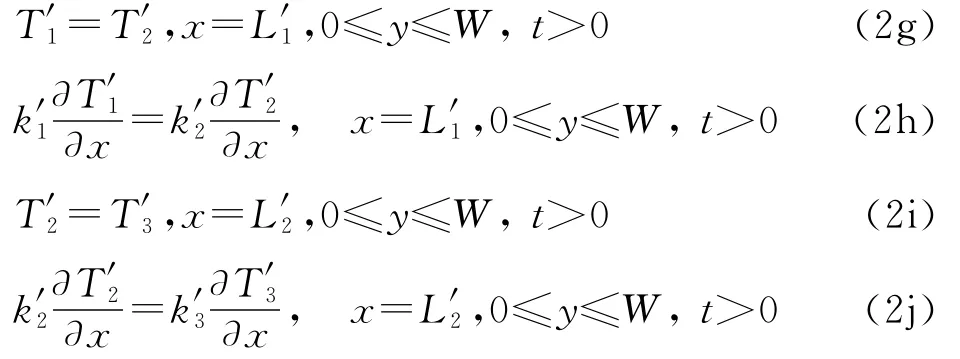
2 传热模型的求解
2.1 开挖面以上埋管传热模型
方程组(1)为带有随时间变化的内热源、非齐次边界条件和初始条件的复合介质热传导问题.对于复合介质在有内热源作用时的传热模型及其解答,国内外已经有了相对成熟的研究.Salt[7-8]给出了二维、各向同性复合板瞬态温度场的解答.Mikhailov等[9]对Salt给出的问题给出了三维解答.Haji-Sheikh,Aviles-Ramos,Yan等[10-15]对多维、多层介质瞬态温度场特征值和特征函数的计算方法进行了研究并给出了在不同边界条件下的解答.Man等基于格林函数法给出了钻孔埋管和桩基内埋管的新模型及解析解[16].笔者基于格林函数法,给出了开挖面以上和以下两部分埋管传热模型的解答.
为求得所需的格林函数,需先求得方程组(1)的齐次形式的解,即

边界条件

连续条件
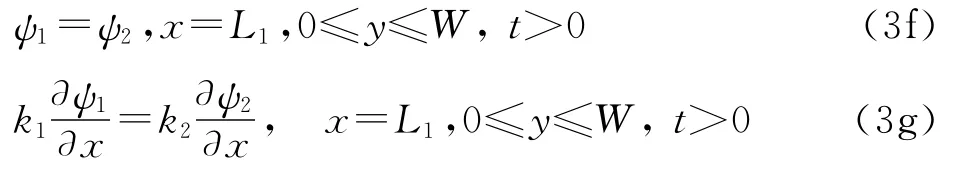
采用分离变量法将ψi分离成空间函数与时间函数.其形式为
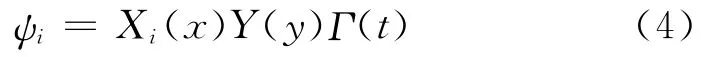
将式(4)代入式(3a),可得

将式(6),(7)代入式(5),可得

由式(6)可以得到函数Y(y)的解为


Ym(y)只对分离参数β取一些特定值,β=βm时才有解,称为特征函数,这些分离的参数值称为特征值.将式(9)代入式(3d),(3e),可得
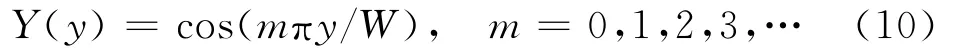
由式(8)可以得到函数X(x)的解为

将式(11)代入式(3b),(3c),(3f),(3g),可得
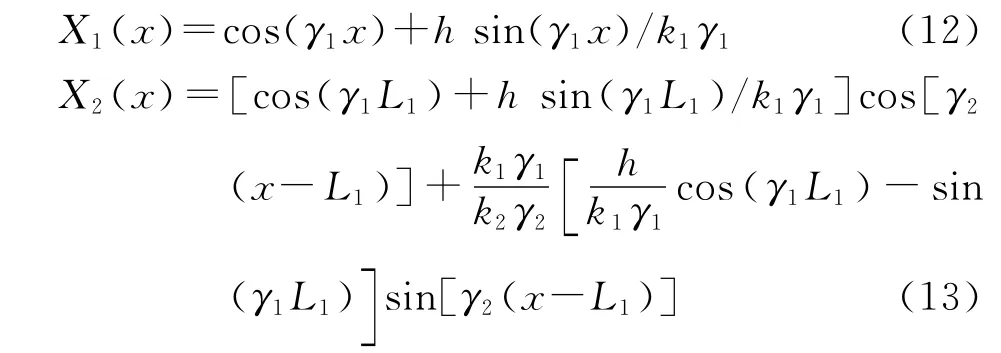
将式(13)代入式(3c)可以求得特征值γi,mn和mn 以及特征函数Xi,mn,i=1,2,m=0,1,2,3,…,n=1,2,3,…,则所需的格林函数为

式中:i=1,2;j=1,2;m=0,1,2,3,…;n=1,2,3,…

最后,方程组(1)的一般解可表示为


式(17)中,Ui(x,y,t)由四项组成,前两项为两个内热源的影响,第3项为对流边界条件(非齐次边界)的影响,第四项为原始地温的影响.当模型中有更多的点热源时,可根据各点热源的坐标和点热源的强度ql(t)按叠加原理求得.
2.2 开挖面以下埋管传热模型
同理,可以得到开挖面以下地下连续墙内埋管传热模型的一般解

Ny,m同式(16).
3 算例分析
3.1 计算参数
以上海自然博物馆为例,对开挖面以上的地下连续墙内埋管进行分析.该馆位于上海市静安区雕塑公园内,周边由山海关路、北京西路、石门二路和成都北路围合.建筑地上3层,地下2层,总建筑面积45086m2.建筑功能主要为展厅,另有藏品室、办公室等辅助用房,地铁13号线从其下部穿越.为了采用可再生能源以节能减排,展厅和藏品库等大空间采用地源热泵系统来承担建筑冬季热负荷和夏季冷负荷.受施工场地限制,地源热泵系统地下换热器布置在地铁连续墙内、自然博物馆外围连续墙内以及自然博物馆地下室范围的灌注桩内.其中,灌注桩埋管393个,有效深度45m;地下连续墙内埋管452个,有效深度为30~38m.
计算模型的尺寸及热交换管的位置见表1.墙体及土体的热物理参数见表2.取混凝土与空气的对流换热系数4.76W·(m2·K)-1,气温18℃,热交换管支管每延米的换热量20W·m-1,墙体及土体原始温度20℃.

表1 计算模型尺寸及热交换管位置Tab.1 Sizes of calculation model and position of heat exchanger tubes m

表2 地下连续墙和土体的热物理参数Tab.2 Thermophysics parameters of diaphragm walls and soil
3.2 计算结果及分析
地下连续墙内埋管模型的解析解具有显式的表达式,借助Mathematica数学软件可以得到任意时刻地下连续墙和土体的温度场分布.运行5,10,20,30d时的地下连续墙内的温度场分布见图4.
本传热模型中,ql(τ)是时间的函数,可以考虑内热源为变热流的情况.表3列出了地下连续墙内埋管三种不同的运行工况,通过傅里叶变换,可以将间歇运行的热流转换为随时间变化的函数[6].

表3 热交换管间歇(连续)运行工况Tab.3 Intermittent(or continuous)operation conditions of heat exchangers

三种不同工况下,某支管的管壁处(x=0.900,y=0.825)温度随时间的变化关系见图5.由图可以看出,间歇运行对于热交换管周围地温恢复、提高地源热泵运行效率显著.

图5 不同运行工况下管壁温度随时间的变化Fig.5 Temperature-time curves of pipe wall in different operation conditions
4 结论
(1)所建立的地下连续墙内埋管换热器开挖面以上和以下两部分的传热模型,可分析带有随时间变化的内热源、非齐次边界条件的复合介质热传导问题,适用于地下连续墙内埋管的实际情况.
(2)由格林函数法推导的地下连续墙内埋管传热模型的解析解,具有显式的表达式,可以求得任一时刻整个计算模型的温度场分布,也可以求得任一点的温度随时间的变化情况.
(3)地下连续墙内埋管传热模型及其解析解,可用于埋管布置形式、埋管间距以及间歇运行时间等参数的优化分析.
[1]夏才初,曹诗定,王伟.能源地下工程的概念、应用与前景展望[J].地下空间与工程学报,2009,5(3):419.XIA Caichu,CAO Shiding,WANG Wei.An introduction to energy geotechnical engineering [J].Chinese Journal of Underground Space and Engineering,2009,5(3):419.
[2]陈小龙,曹诗定.能源地下工程在上海地区的适用性研究[J].土木工程学报,2009,42(10):122.CHEN Xiaolong,CAO Shiding.Applicability of energy saving geo-technology in Shanghai [J].China Civil Engineering Journal,2009,42(10):122.
[3]Brandl H.Energy foundations and other thermo-active ground structures[J].Geotechnique,2006,56(2):81.
[4]Brandl H.Energy piles and diaphragm walls for heat transfer from and into ground [C]//3rd International Geotechnical Seminar,Deep Foundations and Auger Piles III,Ghent:A A Balkema,1998:37-60.
[5]Adam D,Markiewicz R.Energy from earth-coupled structure,foundations,tunnels and sewers[J].Geotechnique,2009,59(3):229.
[6]曹诗定.能源地铁车站主要热交换构件传热计算方法研究[D].上海:同济大学土木工程学院,2009.CAO Shiding.Study on the calculation method of main heaexchangers in energy subway station[D].Shanghai:Tongji University.College of Civil Engineering,2009.
[7]Salt H.Transient conduction in a two dimensional composite slab——I.theoretical development of temperature modes[J].International Journal of Heat and Mass Transfer,1983,26(11):1611.
[8]Salt H.Transient conduction in a two dimensional composite slab——II.theoretical development of temperature modes[J].International Journal of Heat and Mass Transfer,1983,26(11):1617.
[9]Mikhailov M D,öZisik M N,Vulchanov M D.Diffusion in composite layers with automatic solution of eigenvalue problem[J].International Journal of Heat and Mass Transfer,1983,26(8):1131.
[10]Haji-Sheikh A,Beck J V.Temperature solution in multidimensional multi-layer bodies [J].International Journal of Heat and Mass Transfer,2002,45(9):1865.
[11]Aviles-Ramos C,Haji-Sheikh A,Beck J V.Exact solution of heat conduction in composite materials and application to inverse problems[J].Transactions of the ASME,1998,120(3):592.
[12]Haji-Sheikh A,Beck J V,Agonafer D.Steady-state heat conduction in multi-layer bodies [J].International Journal of Heat and Mass Transfer,2003,46(13):2363.
[13]YAN Ling,Haji-Sheikh A,Beck J V.Thermal characteristics of two-layered bodies with embedded thin-film heat source[J].1993,115(3):276.
[14]Feng Z G,Michaelides E E.The use of modified Green’s functions in unsteady heat transfer[J].International Journal of Heat and Mass Transfer,1997,40(12):2997.
[15]Haji-Sheikh A,Beck J V.Green’s function partitioning in Galerkin-base integral solution of the diffusion equation [J].Journal of Heat Transfer,1990,112(1):28.
[16]MAN Yi,YANG Hongxing,DIAO Nairen,et al.A new model and analytical solutions for borehole and pile ground heat exchangers [J].International Journal of Heat and Mass Transfer,2010,53(13-14):2593.
