考虑弯剪耦合作用的梁桥可靠度评估

王晓明，石雪飞，阮 欣

（1.长安大学 桥梁系，陕西 西安 710064；2.同济大学 桥梁系，上海 200092）

在役梁桥量大面广，构造多样，状态各异.对在役梁桥的客观评估是当前桥梁科学管养的重要环节.

梁桥以承受弯矩与剪力为主.现行公路桥规［1－2］将不同功能极限状态直接解耦，采用先分别按照各自极限状态（纯弯、纯剪）独立配筋后再叠加的截面设计方法.

目前的评估方法，继承了设计规范的假设，即认为梁桥破坏是由于纯粹的功能失效，弯剪相互独立，互不影响.现有研究中的弯剪独立串联可靠度法［3－4］、弯剪加权系数组合可靠度法［5］、分项系数法［2，6］等评估方法，都是基于这一假定.该假设忽略了如下客观现实：结构同时承受不同类型荷载内力，提供不同种承载功能，且各种承载功能相互耦合、互为影响［7－8］.以受弯剪为主的梁桥为例，运营中同时承受的弯矩与剪力共同考验着梁的弯剪耦合抗力［9－10］；而理论上的纯弯、纯剪在实际中较少发生.

传统的忽略构件各功能相互影响、极限状态简单解耦的分析方法，在某些情况下会对在役退化旧桥的评估形成误判.笔者以梁桥的弯剪耦合作用为研究对象，分析两种不同功能承载能力间的相互作用，研究考虑弯剪耦合作用的梁桥可靠度评估方法.

1 弯剪耦合作用下梁桥的评估思路

简单地讲，传统评估就是抗力与效应两个值的大小比较.确定性分析，是大小的定量比较；不确定性分析，是大小的随机比较.

当考虑弯剪耦合作用后，抗力与效应由一元变量拓展成二元变量，评估可被描述为判断效应历程与抗力包络区域的位置关系.对于确定性分析，情形较简单，在考虑分项系数、组合系数后，当效应落在抗力所包围的安全区域内，则结构安全，否则不安全.而对于不确定性分析，情况相对复杂，不仅需要判断两者相对位置，而且需要对效应到抗力边界最小距离进行概率度量，以便与目标可靠指标比较.

上述思路中，确定弯剪耦合抗力与弯剪复合效应的概率模型是解决问题的先决条件，而二元随机变量的可靠度分析方法是问题的关键与难点.

2 弯剪耦合抗力的概率模型

2.1 弯剪耦合抗力的分析方法

引入美国AASHTO规范［6］建议的修正压力场理论（MCFT）来分析梁桥的弯剪耦合抗力.它是Bentz等提出的钢筋混凝土分析理论［10］.该方法能够反映弯曲与剪切两种不同功能承载能力间的相互作用，同时考虑了开裂混凝土残余应力，使得抗剪承载力更能反映实际.算法流程如下：

剪切承载力Vn采用式（1）与（2）中较小的

式中：bv为有效腹板宽度；dv为有效抗剪高度；s为箍筋间距；Av为距离s内箍筋面积，为混凝土强度；fy为钢筋的屈服强度；θ为斜压应力的倾斜角；β为斜裂混凝土拉力传递系数.

弯曲承载力采用式（5）与（6）中较小的

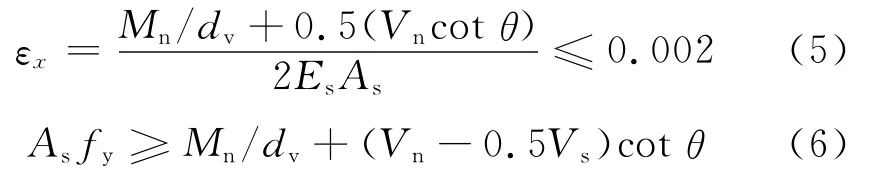
其中：εx为构件弯曲受拉一边的钢筋应变；Mn为弯曲抗力（弯曲承载力）；θ和β是应变εx、剪应力vu（vu＝Vn／（bvdv））和裂缝间距的函数；Es和As分别为抗弯主筋的弹性模量和面积.AASHTO规范中列表给出不同应变εx与不同箍筋应力下的θ，β值.对于给定的箍筋特征参数Avfy／（bvs）与混凝土强度，通过表格线性内插确定不同εx水平下的θ，β值，继而获得弯剪抗力耦合曲线.整个流程见图1.

考虑弯剪耦合作用的确定性分析如图2（图中，SG和SQ分别表示恒、活载效应）.由图可知：

（1）如果不考虑抗力的弯剪耦合作用，只按照纯弯、纯剪抗力值评估，会人为扩大效应的安全区域，将形成较大的误判区域.

（2）对比我国GB 04规范与AASHTO规范可知，计算出的纯弯、纯剪抗力，前者较后者小，明显减小误判区域（图2阴影部分）.这将降低确定性评估的误判几率，但无法消除不确定性评估的差异.如图2，在确定性分析时，效应历程都落在GB 04与AASHTO的抗力包络域，结构安全，评估结论一致；而在不确定性分析时，效应到两种规范的抗力边界最小距离明显不同，概率度量也差异明显，与统一的目标可靠指标比较时，很可能出现不同的评估结论.

图1 弯剪耦合抗力分析流程Fig.1 Analysis process of moment－shear coupling resistance

图2 弯剪耦合抗力与弯剪复合效应的确定性分析Fig.2 Deterministic analysis of moment－shear coupling resistance and effect

对GB 04规范与AASHTO规范的抗力包络域求交集，可将抗力包络域划分为图3所示的4个区域.当弯剪复合效应落在不同的区域，梁桥破坏机制不同：① 在阴影部分，结构安全度较高，可采用传统评估方法；② 浅灰区域时，失效机制为弯曲破坏，关注弯曲承载即可；③ 中灰色区域时，失效机制为剪切破坏，关注剪切承载即可；④ 黑色区域时，失效机制为弯剪破坏，承载力评估需考虑弯剪耦合作用.

2.2 弯剪耦合抗力的概率模型

构件抗力R的概率模型可以表达为

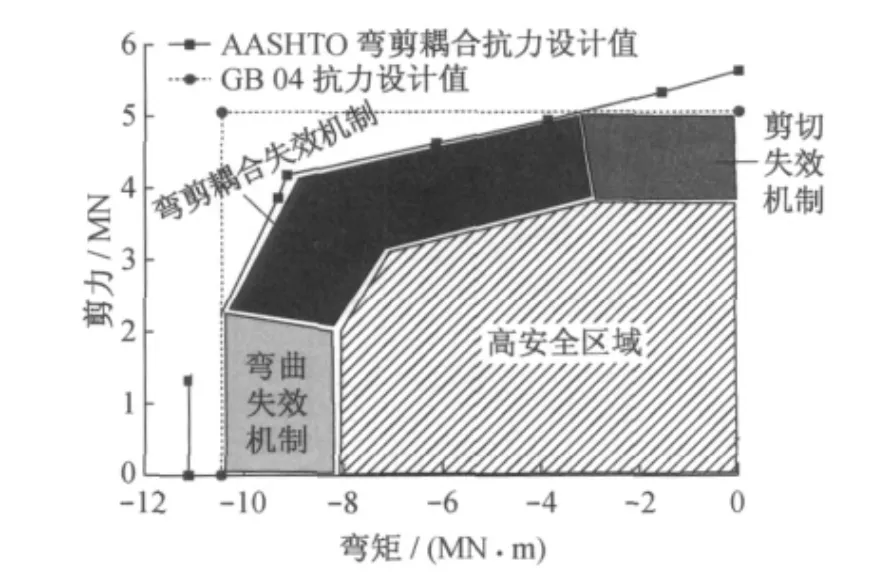
图3 梁桥失效机制划分Fig.3 Failure mechanism types for beam bridge

式中：Rn为名义抗力，由各标准值确定；N为材料特性不定性系数；F为几何参数不定性系数；P为计算模式不定性系数，表示计算近似方法与实际的偏差.

通常认为，N，F，P 服从正态分布，且随机独立［10］.这样抗力R亦服从正态分布，其均值μR有

抗力变异系数δR为

式中：μ为均值，μN，μF，μP分别为N，F，P 的均值；δ为变异系数，δN，δF，δP分别为N，F，P 的变异系数；κR为抗力均值系数.

N和F可采用相关研究［11］建议值；或按照基于Monte－Carlo的抗力概率模型流程［12］，由评估对象的实测数据统计获得；P需要与所用的抗力理论与算法相匹配.研究表明［13］，AASHTO规范中 MCFT公式相应的μP＝1.1，δP＝0.074.因此，根据式（8）和（9）即可确定弯剪耦合抗力的概率模型，见图4.

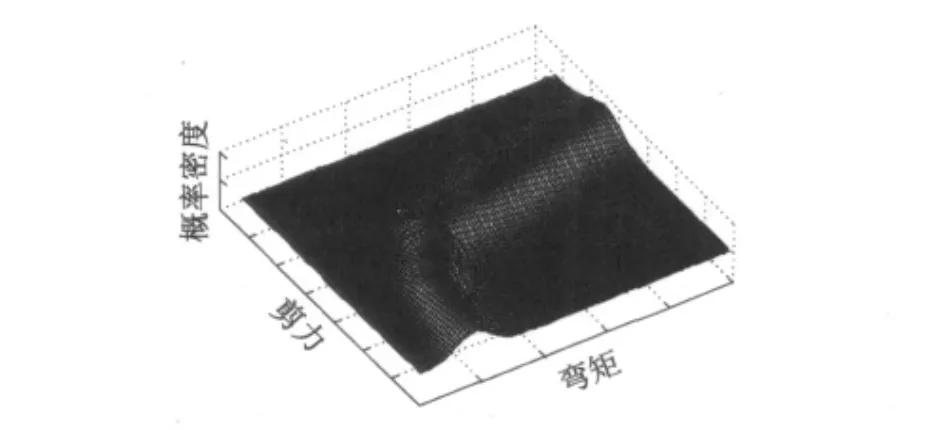
图4 弯剪耦合抗力的概率密度图Fig.4 Probability density of moment－shear coupling resistance

从图4可见，考虑弯剪耦合作用后，抗力从一元随机变量变为二元随机变量，相应的概率密度也由平面正态曲线拓展为空间多段正态曲面，导致二元随机变量可靠度分析变复杂.

3 弯剪复合效应的概率模型

在恒载及车辆活载的作用下，梁桥同时产生弯剪效应；同一截面，弯剪效应的变化强相关，共同取决于加载位置.当分析中考虑了弯剪耦合作用时，效应需要采用弯剪复合的形式来表达，这时，效应S是二元随机变量（SM，SV）.

在已有研究［3－4，14－15］中，车辆的活载效应随机变量的分布常采用最大极值I型来描述.同时，我国公路可靠度标准［16］研究也表明，活荷载效应也不拒绝正态分布.考虑到二元随机变量可靠度分析过程的复杂性，本文采用正态分布描述活载效应.因此，根据标准［16］，可用表1的概率模型分别描述各类效应.

表1 荷载效应概率模型Tab.1 Probability model of load effect

由表1知，恒、活载效应（SG，SQ）都服从正态分布，故定义总效应S＝SG＋SQ，便可用单一变量来描述效应项.此时，总效应S自然也服从正态分布，其均值μS和标准差σS分别如下：

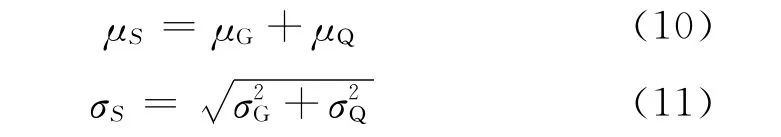
4 考虑弯剪耦合作用的可靠度分析法

建立如下极限状态方程：

R与S相互独立.区别于一元随机变量的极限状态方程，考虑弯剪耦合作用时，R与S都是二元变量.

可靠度分析方法采用可靠指标β考虑随机变量的2阶统计量.在标准正态空间下，β的几何意义是极限状态曲面与原点的最小距离.因此，在普通正态空间下，极限状态方程的β可由图5表示.图中，d代表从控制效应均值点到抗力包络线均值的距离，σZ代表极限状态Z的标准差，m为抽样数.

对弯剪复合随机效应的均值历程进行数值搜索，确定控制效应点后，采用以下公式求得考虑弯剪耦合作用的可靠指标：

图5 弯剪耦合可靠度计算图示Fig.5 Rated figure of moment－shear coupling reliability

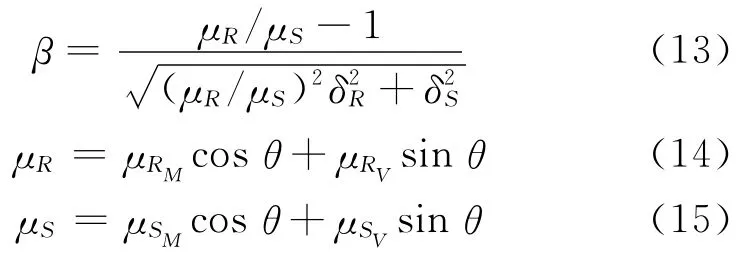
式中：θ为弯矩方向（水平轴）与距离d方向的夹角；μRM，μRV分别为耦合抗力均值的弯矩、剪力分量；μSM，μSV分别为复合效应均值的弯矩、剪力分量；δR，δS分别为耦合抗力、复合效应的变异系数.

5 算例

算例选用交通行业标准——整体式钢筋混凝土4×16m的连续板桥（JT／GQB 008－96），横断面见图6.采用C25混凝土，设计荷载汽车－20级，挂车－100.现评估该类桥型的次中支点截面（支座B处）的承载能力.

（1）弯剪耦合抗力

图7示出弯剪耦合抗力的设计值与标准值，图例括号中“B”代表标准值，“S”代表设计值.

图7 弯剪耦合抗力Fig.7 Moment－shear coupling resistance

依据标准［16］，对材料与几何参数随机变量描述如表2，分布类型皆为正态.

表2 材料与几何参数随机变量Tab.2 Material and geometric parameters random variables

由上述输入参数的概率模型，采用Monte－Carlo法抽样1000次，确定截面B（支座B）在纯弯、纯剪下的材料特性不定性系数N和几何参数不定性系数F，如表3.根据式（8），（9），可确定抗力概率模型的统计参数R，见表4.应用表4的抗力概率模型，确定不同规范的抗力均值曲线，以及纯弯、纯剪下的抗力抽样统计，如图8所示.

表3 材料特性和几何参数不定性系数Tab.3 Uncertainty factor for material properties and geometric parameters

表4 抗力概率模型Tab.4 Probability model of resistance

（2）弯剪复合效应

通过有限元分析，分别确定恒载和汽车－20作用下截面效应标准值，进而根据表1和式（10）及（11）确定总效应S的概率模型.图9给出恒、活载总效应均值时程，由图可见，弯矩、剪力峰值未同时出现，任何单一峰值对应的弯剪状态往往并非控制效应.

图9 恒、活载总效应均值时程Fig.9 Temporal process of mean effect of dead and live load

（3）可靠度评估

按照本方法，对目标截面进行考虑弯剪耦合作用的可靠度评估；作为对比，同时按照传统的弯剪独立串联可靠度方法［3－4］计算，如图10所示.

图10 目标截面可靠度评估Fig.10 Reliability assessment for the target section

对比柱1与柱2（图10柱状图的左起第1、第2个）发现：当采用考虑弯剪耦合作用的可靠度方法分析时，该截面在最不利荷载下的失效机制为弯剪破坏，可靠指标β＝4.75.而采用传统评估方法时，截面受最不利弯矩控制，失效机制为弯曲破坏；串联相应的弯曲与剪切两种失效机制的失效概率后，β＝5.18.两者差异的主要原因是：两种算法的控制效应不同，效应控制点与抗力边界的最小距离相异.

对比柱2与柱3（图10左起第2、第3个柱）发现，都采用传统评估方法时，AASHTO规范抗力所得的可靠指标高于GB 04规范.这是由于GB 04规范在纯弯、纯剪时的抗力值较低.

对比可见，对于复合效应中弯矩、剪切分量都较大的截面，传统评估方法偏不安全；尤其是对于落入图3中黑色区域的复合效应，可能导致错误的评估结论，造成维护决策失误.

（4）参数分析

分别采用本方法与传统的弯剪独立串联可靠度方法，考察在不同弯剪复合抗力作用下截面的可靠指标变化情况.

当效应弯矩分量SM恒定（8MN·m）时，可靠指标β随剪力分量SV的变化见图11a.可见，当剪力小于3MN时，本方法计算的β大于传统方法；在效应处（弯矩为8MN·m，剪力为2MN）发生突变，是由于该点对应的抗力边界与前2个效应点不同；当剪力大于3MN后，本方法计算的β小于传统方法.同理，将SV恒定（4MN）时，β随SM的变化示于图11b.可见，本方法计算的β小于传统方法.

图11 β分别与SV和SM的关系Fig.11 Relationship between moment effect component and reliability indexβ

综上，当控制截面的复合效应弯、剪分量都较大时，传统的弯、剪独立串联可靠度方法偏于不安全，需要采用考虑弯、剪耦合作用的可靠度评估方法.

6 结论

（1）若不考虑抗力的弯剪耦合作用，只按照纯弯、纯剪抗力值评估，会人为扩大效应的安全区域，形成较大的误判区域.由于可靠指标反映了效应与抗力边界的距离，这一点在不确定性分析中体现得更为明显.

（2）对于复合效应中弯矩、剪切分量都较大的截面，其失效机制是弯剪耦合破坏，传统的弯剪独立串联可靠度法结果偏不安全，可能导致错误的评估结论，引起维护决策失误.此时，需要采用考虑弯剪耦合作用的可靠度评估方法.

［1］中交公路规划设计院.JTG60—2004 公路桥涵设计通用规范［S］.北京：中国计划出版社，2004.China Highway Planning and Design Institute.JTG60—2004 Highway bridge design general specification［S］.Beijing：China Planning Press，2004.

［2］中交公路规划设计院.JTG62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京：中国计划出版社，2004.China Highway Planning and Design Institute.JTG62—2004 Reinforced concrete and prestressed concrete highway bridge design specifications ［S］. Beijing： China Planning Press，2004.

［3］Estes A C，Frangopol D M.Repair optimization of highway bridges using system reliability approach［J］.Journal of Structural Engineering，1999，125（7）：766.

［4］Akgul F，Frangopol D M.Lifetime performance analysis of existing steel girder bridge superstructures［J］.Journal of Structural Engineering，2004，130（12）：1875.

［5］高谦，吴顺川，万林海.土木工程可靠性理论及其应用［M］.北京：中国建材工业出版社，2007.GAO Qian，WU Shunchuan，WAN Linhai.Reliability theory and application in civil engineering［M］.Beijing：China Building Materials Industry Press，2007.

［6］American Association of Seate Highway and Transportation Officials.Load and resistance factor bridge design specification［S］.Washington：AASHTO，1994.

［7］Jaswant N，Arlekar C V R.Murty shear moment interaction for design of steel beam－to－column connections［C］／／13th World Conference on Earthquake Engineering.Vancouver：The Canadian Association for Earthquake Engineering，2004.

［8］Mostafaei H，Vecchio F J，Kabeyasawa T.A simplified axialshear－flexure interaction approach for load and displacement capacity of reinforced concrete columns［C］／／ASCE Conference Proceeding on Improving the Seismic Performance of Existing Buildings and Other Structures.［S.l.］：ASCE，2009：69－79.

［9］Hamutçuogˇlu O M，Scott M H.Finite element reliability analysis of bridge girders considering moment－shear interaction［J］.Structural Safety，2009，31（5）：356.

［10］Bentz E C，Vecchio F J，Collins M P.Simplified modified compression field theory for calculating shear strength of reinforced concrete elements［J］.ACI Structural Journal，2006，103（4）：614－624.

［11］交通部公路规划设计院公路桥梁可靠度研究课题组.公路桥梁可靠度研究［R］.北京：交通部公路规划设计院，1994.Highway Bridge Reliability Research Group.Reliability of highway bridges［R］.Beijing：Highway Planning and Design Institute of Ministry of Communications，1994.

［12］石雪飞，王晓明，阮 欣.考虑空间变异性的在役钢筋混凝土梁桥失效概率评估［J］.土木工程学报，2011，44（6）：74.SHI Xuefei，WANG Xiaoming，RUAN Xin.Failure probability assessment of existing RC beam bridges considering spatial variability［J］.China Civil Engineering Journal.2011，44（6）：74.

［13］Turan T O，Higgins C，Rosowsky D V.Statistical modeling of coupled shear－moment resistance for RC bridge girders［J］.Journal of Bridge Engineering，2008，13（4）：351.

［14］贡金鑫.工程结构可靠度计算方法［M］.大连：大连理工大学出版社，2003.GONG Jinxin.Reliability calculation method in engineering structural［M］.Dalian：Dalian University of Technology Press，2003.

［15］应天益.基于WIM数据的桥梁汽车荷载及其效应分析［D］.上海：同济大学桥梁系，2009.YING Tianyi.Analysis on traffic load effects on bridges based on WIM Data［D］.Shanghai：Tongji University.Department of Bridge Engineering，2009.

［16］交通部公路规划设计院.GB／T50283—1999 公路工程结构可靠度设计统一标准［S］.北京：中国计划出版社，1999.Highway Planning and Design Institute of Ministry of Communications.GB／T 20283—1999 Unified Standard for reliability design of highway engineering structures ［S］.Beijing：China Planning Press，1999.