改进的灰色模型在我国农村人均纯收入预测中的应用

2012-10-28陈友余

湖北经济学院学报·人文社科版 2012年3期

关键词：纯收入灰色程度

陈友余

（湖南财政经济学院工商管理系，湖南长沙410205）

改进的灰色模型在我国农村人均纯收入预测中的应用

陈友余

（湖南财政经济学院工商管理系，湖南长沙410205）

以扩展我国农村人均纯收入预测方法和提高预测精度为目标，采用变起点对传统GM（1，1）模型进行改进，改进过程为建立一个预测模型群，改进结果为从预测模型群中挑选精度最高、拟合程度最好的模型作为预测模型，通过实际应用的确提高了预测精度和拟合程度，较大地增强了预测的可操作性和可信性。

GM（1，1）；变起点GM（1，1）；农村人均纯收入

一、引言

农业是国民经济基础，农民问题是“三农”工作的重心。农村人均纯收入呈现持续增长的同时,城乡收入差距较大,影响和制约农民收入增长的因素仍然存在。基于此，本文依据2000～2010年农村人均纯收入数据，运用改进的灰色模型对我国农村人均纯收入进行预测。

灰色系统理论是邓聚龙教授首次提出的，解决了学术界一直无人解决的微积分方程建模问题。其研究对象是“部分信息已知，部分信息未知”的小样本、贫信息的不确定性系统，具有建模过程简单，建模表达式简洁等优点，被广泛应用于经济、生物、农业、医药、水利等领域，但其模型有一定的缺陷，不少学者对其进行了一定程度的改进，残差GM（1，1）模型在实际应用广泛。本文在传统GM（1，1）模型的基础上采用变起点方法进行改进，建立了一个预测群，从预测群中挑选最优的模型用于预测，这种方法一方面提高了预测精度和拟合程度，一方面增强了预测的可操作性和实用性。

二、传统GM（1，1）模型

GM（1，1）模型是指，对原始时间序列进行一次累加，从而生成的序列具有强递增特性，然后建立相应的近似微分方程，来体现序列的发展规律。其方法如下：

（一）原始时间序列 x（0）=（x（0）（1），x（0）（2），…，x（0）（n）），其中n为原始数据个数，对x（0）进行一次累加生成序列x（1），即IAGO，得：x（1）=（x（1）（1），x（1）（2），…，x（1）（n）），其中（i），其中i=1，2，…，n（以下不做特殊说明，i的取值与此相同）。

（二）检验x（0）的准光滑性和x（1）的准指数规律。准光滑系数时一般认为满足准光滑条件；准指数规律指标一般认为满足准指数规律。

（三）若p（i+1）<0.5，σ（1）（i）缀[1，1.5]，则GM（1，1）的白化微分方程为其中，-a为发展灰度，b为灰色作用量，a、b均为待定系数；t表示时间；由于x（1）（i）与灰导数不满足平射关系，本文采用传统方法对序列x（1）采用紧邻均值生成序列 w（1），即w（1）=（w（1）（1），w（1）（2），…，w（1）（n）），其中w（1）（i+1）=0.5x（1）（i）+0.5x（1）（i+1）。于是白化微分方程对应的灰微分方程为：x（0）（i）+aw（1）（i）=b.

于是x（0）（i）+aw（1）（i）=b可等价变形为：Y=BA，对于两个未知系数（a与b）的n-1个方程是无解的，此时考虑利用最小二乘法近似得到A赞=（BTB）-1BTY，可求出近似解a赞，b赞。

（五）将a赞，b赞代入灰微分方程，求得离散响应函数：

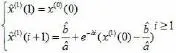
（六）对x赞（1）（i+1）进行累减还原，得到原始数据的预测值：

（七）精度检验

（八）拟合度检验

灰色关联分析是通过确定原始序列和预测序列的几何形状的相似程度来判断其紧密程度，从而对原始序列动态发展态势进行量化比较分析。其步骤是将预测序列与原始序列进行无量纲化处理，计算关联系数和关联度，再根据关联度的大小判定紧密程度。

第1步，变量的无量纲化，求原始序列与预测序列的初值像（或均值像），本文选用初值像；

ρ为分辨系数，ρ越小，分辨力越大，当ρ燮0.5463时，分辨力最好，通常取ρ=0.5，本文也取ρ=0.5。

三、变起点GM（1，1）模型

在实际预测建模中，不一定用原始序列中全部的数据来建模。在原始序列中有规律挑选一部分数据（数据至少为4个），就可建立一个模型。为了提高传统GM（1，1）模型的预测精度和拟合程度，建模数据中应为包含x（0）在内的一个等时距序列，基于这种思想，以x（0）为建模取值的终点，从后往前不断取值，可以建立一个预测模型群，从预测模型群中挑选最优的模型用于以后的预测，其建模和求解如下：

1.给定原始时间序列x（0）=（x（0）（1），x（0）（2），…，x（0）（n）），其中n为原始数据个数；

2.用x（0）=（x（0）（1），x（0）（2），…，x（0）（n））建立的GM（1，1）模型为全部数据模型；用x（0）=（x（0）（i），x（0）（i+1），…,x（0）（n））（i叟2）建立的GM（1，1）模型为部分数据模型；

3.由于最短时间序列中数据至少为4个，于是可建立一个4维子序列：（x（0）（n-3），x（0）（n-2），x（0）（n-1），x（0）（n）），依次往下，最后可建立一个n维子序列（即原时间序列），总共可建立n-3个子序列；

4.对各子序列按传统GM（1，1）模型方法进行预测，并进行精度检验和拟合度检验，从模型群中挑选最优的模型应用于预测。

四、改进的灰色模型在我国农村人均纯收入预测中的应用

21世纪开局以来，我国农村人均纯收入见下表，数据均来至于《全国国民经济和社会发展统计公报》。

表1 ：我国2000~2010年农村人均纯收入（单位：元）

（一）构建传统GM（1，1）模型

首先建立我国农村人均纯收入序列，同时对x（0）进行一次累加生成序列x（1），即I-AGO，计算过程在此不赘述；然后检验x（0）的准光滑性和x（1）的准指数规律。当i＞2时，p（i）<0.5，σ（1）（i）缀[1，1.5]，满足准光滑性和准指数规律要求，构造矩阵B和常数矩阵Y；再应用Excel中的LINEST可求出a赞=-0.1107，b赞= 1773.23；将a赞，b赞代灰微分方程，求得离散响应函数，在此基础上，对进行累减还原，得到原始数据的预测值，最后进行精度检验，通，s1=过计算，平均相对误差，可见可见后验差比值c<0.35，小误差频率P=1，关联度为0.6366，可见预测误差的一般水平很低，预测误差摆动的幅度小，误差较小的概率达到了100%，可知精度高，能达到拟合要求。可见，我国2000~2010年农村人均纯收入序列能完全通过检验，可用于预测。

（二）变起点GM（1，1）模型

1.由于n=11,故可建立8个子序列。

2.对各子序列按传统GM（1，1）模型方法进行预测，得各模型对应的离散响应函数；通过计算平均相对误差、后验差比值和小误差频率和灰关联度，对各子模型进行精度比较和拟合程度比较：平均相对误差方面，11维子序列达到1级精度，5维子序列达到3级精度，其余子序列达到2级精度，2级精度由高到低顺序为：4维子序列最高，6维子序列，8维子序列和9维子序列次之，然后是10维子序列，最后是7维子序列；后验差比值方面，各子序列均达到了1级精度，精度由高到低顺序为：9维子序列，8维子序列，10维子序列，6维子序列，5维子序列，11维子序列，4维子序列，7维子序列；小误差频率方面，各子序列均达到了1级精度；拟合度检验方面，15维子序列及4维子序列拟合程度不满意，其余均满意，满足条件的子序列拟合程度由高到低顺序为：8维子序列，7维子序列，10维子序列,11维子序列，9维子序列，6维子序列和8维子序列，综合以上比较，选择8维子序列作为预测模型。