带负顾客和启动时间Bernoulli反馈M/M/1工作休假排队

朱少平，王 珍

带负顾客和启动时间Bernoulli反馈M/M/1工作休假排队

*朱少平，王 珍

(井冈山大学数理学院，江西，吉安 343009)

在Bernoulli反馈的情形下考虑带有负顾客和启动时间的M/M/1工作休假排队模型，画出了状态转移图，给出了无穷小生成元，利用拟生灭过程与矩阵几何解方法，得到了稳态队长和稳态等待时间的分布。另外，还得到了队长和等待时间的条件随机分解结构及附加队长和附加延迟的分布。

负顾客；Bernoulli 反馈；启动时间；工作休假；随机分解

工作休假是一种半休假策略，由文献[1]首次提出，相关的研究还有文献[2-3]。文献[4]综合研究了排对论中的负顾客，带有反馈的排队系统在生产和实际生活中都有很重要的意义，带反馈的排队系统与经典排队系统的服务机制相比所有变化，顾客到达系统后并不一定经过一次服务就离开系统，可能经过多次，这个服务次数是由反馈机制所决定的。带反馈的服务系统的研究为实际工作中遇到的具体模型提供了一种有利的数学工具，文献[5-6]中有相关的模型研究，其中Bernoulli反馈已被广泛应用于计算机分时操作系统和无线电通讯网络系统中，通过对其某些指标的研究，可安排最合理的方案。

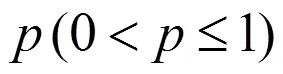
1 模型的描述

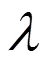
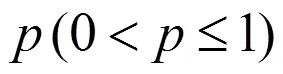
（4）服务员对正顾客在正规忙期和工作休假期的服务时间分别服从参数为1和2的负指数分布，其中2＜1；

（5）当一次工作休假结束时，如果系统中有正顾客，服务台立即转入正规忙期对顾客进行服务，服务率由2变为1，一个正规忙期开始，此时正在接受服务的正顾客重新开始接受服务；若一个工作休假结束时系统中没有正顾客，服务台就进入一个关闭期；

（6）若在关闭期内有顾客到达，则关闭期结束，但正顾客不能立即接受服务，需经历一个启动期，启动时间服从参数为α的负指数分布，启动期结束后进入正规忙期；

（7）假设正、负顾客的到达间隔，工作休假时间，启动时间，正规忙期和工作休假期的服务时间均相互独立，服务规则为FCFS。

设()表示时刻系统中的正顾客数，定义()如下