改进人工蜂群算法

毕晓君，王艳娇

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

Karaboga于2005年成功提出了解决函数优化问题的人工蜂群算法(artificial bee colony algorithm，ABC算法)［1］，并与差分进化算法、粒子群算法等进行了比较，确定了ABC算法在函数优化方面的优越性，算法无需设置很多参数，操作简单，特别适合工程应用.然而，作为一种新的搜索算法，它的理论研究尚处于初级阶段，文献［2-3］分别引用联赛选择和boltzmann选择方式代替ABC算法中的轮盘赌选择方式;文献［4］引入遗传交叉因子增加种群多样性，都在一定程度上降低了陷入局部最优的可能，但收敛速度和精度并不高.为此，本文通过深入研究，借鉴自由搜索算法中提出的信息素、灵敏度模型代替轮盘赌方式进行选择并引入OBL策略提出一种改进的人工蜂群算法，在此基础上，结合NIT技术提出一种新的多峰优化方法.优化9个被广泛选用的标准测试函数及5个多峰函数优化实例.

1 人工蜂群算法

ABC算法模拟实际蜜蜂采蜜机制处理函数优化问题，将人工蜂群分为3类:引领蜂、跟随蜂和侦查蜂，引领蜂、跟随蜂用于蜜源的开采，侦查蜂避免蜜源种类过少［1］.优化问题的解及相应的函数值抽象为蜜源的位置和花蜜的数量.寻找最优蜜源的过程如下:随机产生2N个位置，取较优异的N个作为蜜源位置，引领蜂发现蜜源并记忆，在各蜜源附近按式(1)搜索新蜜源:

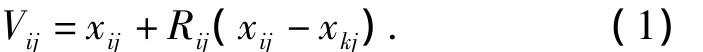
式中:Vij为新的蜜源位置，xij为蜜源的第j维位置，xkj为随机选择的不等于i的蜜源的第j维位置，Rij为［－1，1］间的随机数.

根据前后蜜源的花蜜数量(适应度值)选择较优蜜源并作为初始标记蜜源;引领蜂释放与标记蜜源质量成正比的信息，用来招募跟随蜂，跟随蜂利用轮盘赌方式取合适的标记蜜源并在其附近按式(1)搜索新蜜源，并与初始标记蜜源进行比较，选取较优异的蜜源更改本次循环的初始标记蜜源.但是如果在采蜜过程中，蜜源经若干次搜索不变，相应的引领蜂变成侦查蜂，随机搜索新蜜源代替初始标记蜜源中的相应位置，确定最终蜜源.按照上述方式反复循环迭代，直到达到算法的终止条件.

为了更进一步了解ABC算法，图1给出了算法的程序流程.

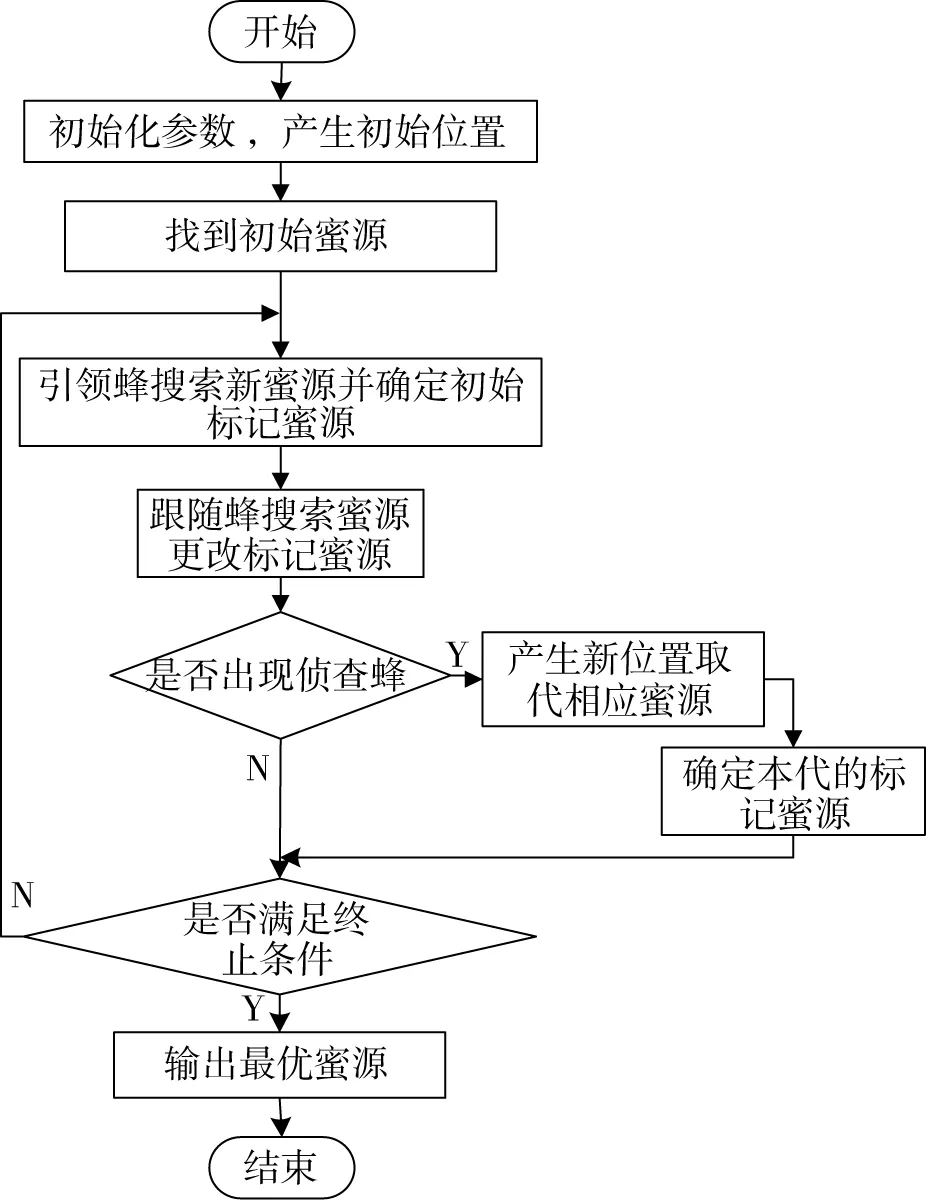
图1 ABC算法流程图Fig.1 Flowchart of ABC algorithm

2 改进的人工蜂群算法

人工蜂群算法函数优化效果较好，但由于采用轮盘赌选择方式使算法易陷入局部最优，而在迭代的过程中，每代的最差解会参与新解的产生从而影响了算法的收敛速度.为此，本文在选择策略、最差解的替换方法方面做了改进.

2.1 选择策略的调整

在ABC算法中，跟随蜂选择蜜源时依据轮盘赌方式，这是一种基于贪婪策略的选择方式，会使种群多样性降低，从而引起过早收敛和提前停滞的现象.在自由搜索算法中，提出了一个重要概念——灵敏度，通过与信息素(与优化问题的适应度值有关)配合选择区域，理论上可以搜索任何区域，这就在很大程度上避免了陷入局部最优;所搜索区域的信息素必须适应其灵敏度，这就使算法有导向作用，决定了目标函数在搜索空间中的收敛和发散.这种区域选择的方式与跟随蜂选择蜜源的方式是类似的，所以可以考虑将灵敏度与信息素配合的方式代替轮盘赌方式选择蜜源.具体过程如下:

1)计算N个蜜源的适应度值f(X).

2)计算第i个蜜源的信息素nf(i):

3)随机产生第 i个跟随蜂的灵敏度 S(i)～U(0，1).

4)找出配合第i个跟随蜂灵敏度的蜜源:随机找出 i，满足 nf(i)≤S(i).

2.2 最差蜜源的替换

在ABC算法迭代的过程中，引领蜂和跟随蜂都可能依赖本代的最差蜜源按式(2)进行交叉操作产生新蜜源，但最差蜜源几乎不可能对需要的最优结果做出贡献，这就在一定程度上影响了算法的收敛速度.因此可以考虑产生一个新蜜源替换最差蜜源.鉴于文献［11］已从数学上证明:依靠产生候选解的相对点取代原候选解的OBL策略是对原候选解的一种较好估计，与产生随机点代替原候选解的方式相比，通常会取得更佳的优化效果，不仅大大提高了收敛速度，而且在一定程度上避免了陷入局部最优.因此引用文献［6］提出的OBL策略产生新蜜源取代最差蜜源.具体方式如下:

在每代循环中，找到最差蜜源，对应位置为Xb.引用OBL后的新蜜源位置为则新位置的第j维X＇为bj

如果新位置对应的蜜源更佳，则用其代替原蜜源位置.

2.3 基于改进人工蜂群算法的多峰函数优化

文献［12］运用NIT技术识别小生境范围，结合适应值共享小生境计算共享适应度值，指导遗传算法的种群进化，使种群多样性不至于过少，用以解决多峰函数优化问题.该方法也存在不能求得所有峰及峰值点定位不准确的缺陷.究其原因，随着种群的进化，个体分布不再均匀，使得某些峰所在范围内的个体数目较少，如图2所示.按照NIT技术的方法，会使得这2个小生境被规划为一个小生境从而造成漏峰的现象.可见，个体的分布情况严重影响小生境的识别效果.而随着进化的进行，很难保证可行域内的个体分布均匀，即图2所示的情况很容易出现，这也是造成漏峰现象的一个主要原因.

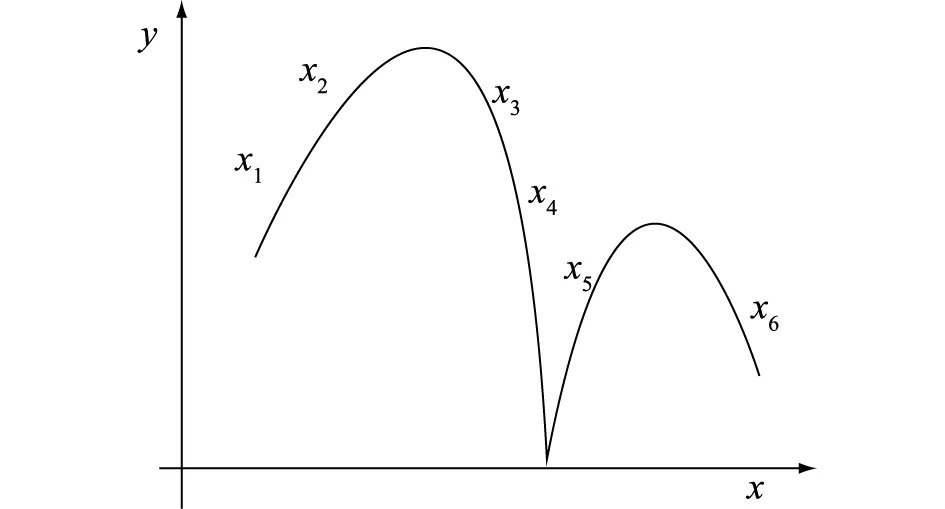
图2 个体分布情况Fig.2 Distribution of individuals

为避免这种现象的产生，结合NIT技术和改进的人工蜂群算法设计一种新的多峰优化方法，即:

首先，在可行域内产生大量均匀分布的点，利用NIT技术划分可行域为若干个小生境;然后，在各个小生境内独立运行人工蜂群算法若干次，以便精确锁定各个小生境内的峰值点.与现有利用NIT技术解决多峰函数优化问题的方法相比:本文方法不与其他方法结合指导种群进化，避免了在进化过程中，因多样性分布不均而造成的如图2所示的现象，有效的避免了漏峰.

由于小生境范围大小相差较大，如果在各小生境内预设相同数目的个体进行进化就会造成较大范围的小生境在固定迭代次数内未收敛，而较小范围的小生境早就收敛、浪费时间，为此，自适应调节各小生境内的个体数目如下:

其中，n为测试问题的维数;BiH，BiL分别代表第i维小生境的边界;r为一个人为设定的步长.上式代表某小生境内的个体数目为在该范围的长度与步长相除取整.为避免某小生境内的个体数目过少，令该范围内的个体数目为一人为设定的常数.

为了更好地了解该方法，下面给出本文提出的多分函数优化方法的实现步骤:

1)在定义域内设定较小步长，产生均匀分布的个体.

2)依据改进的NIT技术对种群进行小生境的识别，记录各个小生境每维的上下限.

3)在各个小生境内执行改进的人工蜂群算法:

①初始化，设置相关的实验参数，如引领蜂、跟随蜂的最大种群大小，最大的迭代次数.

②确定小生境内的种群大小，并在小生境指定的范围内产生随机分布的个体.

③选择初始种群中较优的一半个体作为初始标记蜜源.

④引领蜂随机选择蜜源并与自身蜜源进行交叉产生新的位置，与原位置进行比较，择优标记蜜源.

⑤跟随蜂在蜜源中按照2.1中的新选择方式选择合适蜜源进行交叉操作产生新的位置.

⑥选择和④⑤中的较为优秀的个体作为本代的标记蜜源.

⑦判断是否达到了最大的迭代次数，如果达到记录最优位置并转到5)，否则转至②.

4)判断是否遍历完所有小生境，如果已遍历完转至5)，否则更改小生境范围，转至3).

5)输出各小生境的最优位置.

3 实验仿真与结果分析

先验证提出改进算法(以下简称为FSABC算法)性能及应用效果，需进行大量仿真实验.实验仿真是在 Intel Centrino Duo，CPU:T7250、1G 内存、2.0 GHz主频的计算机上实现，程序采用 Matlab7.5语言实现.

3.1 FSABC算法的函数优化性能

表1 测试函数Table 1 Test function

为验证本文提出的FSABC算法的函数优化效果好坏，选用函数优化领域被广泛采用的9个标准测试函数［10］进行测试，表1给出了这些测试函数的定义、取值范围，它们的理论最优值都为0.并将其与ABC算法及目前改进效果较好的ABCP算法［9］进行了对比.

函数1～4是连续型单模态函数，函数5为非连续的单模态函数，它们主要用来测试算法的寻优精度，考察执行性能;函数6为噪音函数，很难收敛到全局最优解，其余函数都为复杂的多模态函数，有许多局部极值点，一般算法都难于找到全局最优值，因此可用来检测算法的全局搜索性能和避免早熟的能力.

算法具体参数设置如下:引领蜂、跟随蜂和蜜源的数量都为50;测试函数都取50维;limit为10;各函数迭代1 000次.为了测试算法性能优劣，针对每个测试函数，各算法均随机运行50次，选取测试函数的最优值、最差值、平均值、方差、平均运行时间(即获得最优解的时间)来考察算法的寻优性能.

表2 3种算法的性能比较Table 2 Performance comparison of three algorithms

由表2中数据可以得出以下结论:

1)在寻优性能上，ABC算法在解决不是很复杂的问题(如函数1和2)时，可以取得较好的效果，而在解决较复杂的函数时，基本不会得到满意解;ABCP算法与之相比较，在处理较简单问题时，解的精度有较大提高，但仍未达到理论最优值，而在处理较复杂的多模态函数时，寻优结果并不理想，说明ABCP算法虽有较好的执行性能但易陷入局部最优、全局寻优性能较差;而本文提出的FSABC算法无论处理上述的哪种测试函数，几乎都可以收敛到理论最优解，而且算法较稳定.由此可见，本文算法更容易跳出局部最优，具有良好的全局搜索能力.

2)在运行时间上，虽然FSABC比ABC算法复杂一些，使迭代一次的时间有所增加，但FSABC算法获得最优解的迭代次数比ABC少得多，因此FSABC算法获得最优解的运行时间比ABC算法短，且比ABCP算法短得多，因此可以说本文算法缩短了运行时间.

为了直观对比这3种算法的性能优劣，图3给出了2个函数的进化过程曲线.

图3 3种算法的进化过程比较Fig.3 The Evolution com parison of three algorithms

由上述的数据比较及进化过程曲线可以得出结论，与目前现有的人工蜂群算法相比，本文提出的算法大大提高了寻优能力，并且缩短了运行时间，具有良好的函数优化效果.

3.2 多峰函数优化效果

为验证本文提出的多峰优化方法是否有效，选取该领域广泛采用的测试函数进行测试，如下:

一维测试函数1在定义域内有9个不等高不等距的峰.

测试函数2 Ackley function在定义域 x，y∈［－3.5，3.5］内有49 个极大值点.

测试函数3该函数是非均匀分布的多峰函数，有一个全局最优值和99个局部极值，其中包含64个山峰和36个在 x，y∈［－2，2］边界上形成的峰值点.一般算法很难搜索到所有峰.

该函数有6个高度为1的全局最优解，在0.5高度处有一个很难突破的平坦区域，可用该函数的平均适应度来评价算法收敛的准确性.

测试函数5

这是一个改进的Himmenblau函数，有一个全局最优解和3个局部最优解，定义域为x，y∈［－6，6］，全局最优解位于(3，2)处，函数值为200.0，而局部最优点位于(3.581 5，1.820 8)、(2.787 1，3.128 2)及(3.763 4，3.266 1)处，对应的函数值分别为198.50，196.51 和 192.63.

测试函数1是较为复杂的一维多峰函数，用以验证算法对于一维函数的优化性能;函数2、3是典型的二维测试函数，具有较多个峰，常用以检测算法识别出的峰数能力;而其余函数用以测试算法的精确性.

对一维函数测试的实验参数设置如下:步长为0.1、各小生境的最少种群数目为8、常数为0.01.仿真结果如图4所示.

测试函数4

图4 一维测试效果Fig.4 The optimization effect one-dimension

从图4可以看出，本文方法非常准确的锁定了各个峰值点，一维多峰函数优化效果很好.

3.3 检测峰数的能力

为了验证本文提出方法具有良好的识别峰数的能力，对函数3进行测试，参数设置为:以横、纵轴的步长都为0.08产生小生境分割所需要的点，各小生境内的最小种群数目为8、常数取为0.001，迭代次数为30.并与文献［13］中方法进行比较，结果见表3.

表3 不同方法对测试函数3的仿真结果Table 3 Performance of function 3 based on several methods

从表中数据可以看出，与另外3种方法相比，该方法可以搜索到较多的峰，且需要较少的迭代次数.这是因为在初始阶段NIT技术可以较为准确的识别各个小生境，从而自动的划分成多个种群，就不会因进化的趋向性使种群多样性降低，因此具有较高的识别峰的能力.而对于Opt-aiNet算法，当目标函数的峰值较密集且大于种群规模时，开拓搜索空间的能力就会较差，不易搜索到所有峰值.

不失一般性，用该方法对测试函数2进行仿真，参数设置及实验条件同上，函数2、3的仿真结果如图5所示，从图5可以直观的看出本文方法具有很好的识别峰数的能力.

图5 二维函数寻优效果直观图Fig.5 The optimization effect of two-dimension

3.4 算法的精确性

为验证提出算法不仅可以搜索到所有的峰还具有较高的寻优精度，对函数4进行测试，参数设置除以横、纵轴的步长都为0.1产生小生境分割所需要的点外，其他条件同上.并将其与文献［4］中方法进行比较，比较结果如表4所示.

表4 不同方法对函数4的仿真结果Table 4 Performance of function 4 based on several methods

从表中数据可以看出，与另外2种较好的多峰优化方法相比，该算法在较少的迭代次数下可以获得更为精确地结果.这是由于在已精确划定小生境范围的基础上，各小生境都是较为简单的形状，而改进的人工蜂群算法是一种非常优秀的函数优化方法，所以精确搜索到各个峰值点也是一个必然的结果.表5给出一次仿真结果.

表5 本文算法对函数4的仿真结果Table 5 Simulation of function 4 based on this method

为了进一步说明提出方法的普遍性，对函数5进行测试，参数设置除以横、纵轴的步长都为0.2，产生小生境分割所需要的点外，其他条件同上.仿真结果见表6.

表6 本文算法对函数5的仿真结果Table 6 Simulation of function 5 based on this method

从表中数据很容易看出本文方法给出的寻优结果十分接近理论值，即具有较高的寻优精度.

综上所述，本文提出基于人工蜂群算法的多模态优化方法不仅具有较好的识别峰数的能力，而且寻优精度较高，是一种行之有效的多峰优化方法.

4 结束语

针对ABC算法易陷入局部最优、收敛速度慢的缺点，本文利用信息素与灵敏度模型实现了概率选择，引入OBL策略改变了每次迭代的最差解，由此提出一种改进的人工蜂群算法——FSABC算法.与传统的ABC算法及ABCP算法相比，该算法获得的最优解精度明显提高很多，而且只需要经过较少次的迭代，也就是说算法的寻优能力得到大幅度提高;在运行时间上，FSABC算法获得最优解的运行时间要比ABCP算法短得多，也比ABC算法短，即本文算法缩短了运行时间.该算法不仅大大提高了算法的寻优能力，而且缩短了运行时间.基于这种函数优化效果很好的改进人工蜂群算法及NIT技术而提出的两阶段多峰优化方法，经实验证实不仅具有较强的识别峰的能力，而且精度很高.由此可见，本文提出的FSABC算法在解决函数优化类问题上优势明显.

［1］KARABOGA D，BASTURK B.On the performance of artificial bee colony(ABC)algorithm［J］.Applied Soft Computing，2008，8(1):687-697.

［2］暴励，曾建潮.自适应搜索空间的混沌蜂群算法［J］.计算机应用研究，2010，27(4):1331-1335.BAO Li，ZENG Jianchao.Self-adapting search space chaos-artificial bee colony algorithm［J］.Application Research of Computers，2010，27(4):1331-1335.

［3］丁海军，冯庆娴.基于Boltzmann选择策略的人工蜂群算法［J］.计算机工程与应用，2009，45(31):53-55.DING Haijun，FENG Qingxian.Artificial bee colony algorithm based on Boltzmann selection policy［J］.Computer Engineering and Applications，2009，45(31):53-55.

［4］罗钧，樊鹏程.基于遗传交叉因子的改进蜂群优化算法［J］.计算机应用研究，2009，26(10):3751-3753.LUO Jun，FAN Pengcheng.Improved particle swarm optimization based on genetic hybrid genes［J］.Application Research of Computer，2009，26(10):3751-3753.

［5］PENEV K，LITTLEFAIR G ，Free Search—a comparative analysis［J］.Information Sciences，2005，172(1):173-193.

［6］RAHNAMAYAN S，TIZHOOSH H R，SALAMA M M A.opposition-Based differential evolution［J］.IEEE Transactions on Evolutionary Computation ，2008，12(1):64-79.

［7］KARBOGA D，BASTURK B.A powerful and efficiental gorithm for numerical function optimization:artificial bee colony(ABC)algorithm［J］.Journal of Global Optimization，2007，39(3):459-471.

［8］TIAHOOSH H R.Opposition-based learning:a new scheme for machine intelligence［C］//Proceedings of International Computational Intelligence for Modeling Control and Automation.Sydney，Australia，2005:695-701.

［9］LIU Xingbao，CAI Zixing.Artificial bee colony programming made faster［J］.Natural Computation，2009(8):14-16.

［10］JANEZ B，SASO G，BORKO B.Self-adapting control parameters in differential evolution:a comparative study on numerical benchmark pro-blems［J］.IEEE Transactions on Evolutionary Comp-utation，2006，12(10):646-657.

［11］RAHNAMAYAN S，TIZHOOSH H R，SALAMA M M A.Opposition versus randomness in soft computing techniques［J］.Applied Soft Computing，2008，8(2):906-918.

［12］陆青，梁昌勇，杨善林，等.面向多模态函数优化的自适应小生境遗传算法［J］.模式识别与人工智能，2009，22(1):91-100.LU Qing，LIANG Changyong，ZHANG Enqiao，et al.An adaptive niche genetic algorithm for multi modal function optimization［J］.Pattem Recognition and Artificial Intelligence，2009，22(1):91-100.

［13］薛文涛，吴晓蓓，徐志良.用于多峰函数优化的免疫粒子群网络算法［J］.系统工程与电子技术，2009，31(3):705-709.XUE Wentao，WU Xiaobei，XU Zhiliang.Immune particle swarm network algorithm formultimodal function optimization［J］.Journal of Systems Engineering and Electronics，2009，31(3):705-709.