遗忘曲线的协同过滤推荐模型

印桂生，崔晓晖，马志强

(哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨 150001)

网络技术的发展带来了信息过载［1］现象.作为一种信息过滤手段，协同过滤推荐系统［2］根据用户对某些资源的历史评价信息，主动提供其可能感兴趣的资源列表.

现有协同过滤推荐系统，如Tapestry System［3］，Grouplens［4］，Yahoo Tomoharu［5］等，将发生于不同时刻下的历史信息等同对待，缺乏对其时效量化分析.一种合理的思维是:距离当前时刻越近的历史评价信息在评价预测中具有更高的推荐效用，反之，距离当前时刻越远的历史评价效用越低，即时效随时间发生衰减［6］.一些研究成果采用线性或非线性衰退函数量化评价时效随时间变化情况.KOYCHEV［7］采用线性函数作为时效量化基础.KUKAR［8］采用核函数计算时效随时间衰减情况.DIND［9］指出时效量化是一个随时间发生梯度逐渐下降过程，故指数函数更加适合时效量化.上述模型虽然一定程度上满足时效随时间发生衰退的基本特征，但没有考虑资源的时效衰退差异性问题.在推荐系统中，用户兴趣漂移［10］普遍存在导致时效衰退程度发生动态改变，表现为受欢迎的资源其时效衰减速率较慢.因此，如何根据用户兴趣，探索时效随时间衰退特征，是提高时效量化在推荐系统中实用价值的主要途径.

基于此，提出一种应用遗忘曲线的协同过滤推荐模型(FC-CFRM:forgetting curve based collaborative filter recommendation model).该模型从用户兴趣漂移角度揭示资源时效遗忘速率的差异化规律，通过多阶段时效量化方法和时间单位映射函数，计算具有记忆特征的历史信息时效值，为合理量化历史信息时效和提高推荐效果提供基础.

1 推荐模型

FC-CFRM 可定义为 6 元组 ＜U，O，R，P，δ，f＞.其中，U={ui}，表示用户集合;O={oj}表示资源集合;R={ri，j}表示用户ui对资源oj的使用评价信息;P={pj(t，k)}表示不同资源的时效量化函数，pj(t，k)є［0，1］，t表示当前时间步，k 控制时效随时间衰减的遗忘速率;δ称为惰性更新因子，δ越大，同一阶段用户反馈对遗忘速率调整越小;f为效用函数，也称推荐预测函数，用于计算用户对于未知资源的推荐值，即f:U×O×T→R.FC-CFRM的目的是找到那些推荐值最高的资源形成评价列表L.例如:针对用户ui，如果令其评价过的资源集合为O*，max为最大值函数，则推荐列表L的形式化表述为

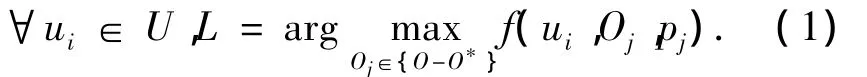
FC-CFRM具体执行过程分为2个阶段:相似度计算和评价预测.

1.1 相似度计算

根据用户资源历史评价信息，相似度计算用于确定不同资源之间的相似程度，为后续评价预测提供基础.常见的相似度计算方法包括:类欧式距离法，条件概率法和皮尔森法.

1.1.1 类欧式距离法

将资源看作是用户评价流形子空间中的点，资源间相似程度由点间距离决定.点间距离越大，相似度越低.如果令U(a，b)表示同时参与评价资源oa和ob的用户集合，则类欧式距离法计算过程表示为

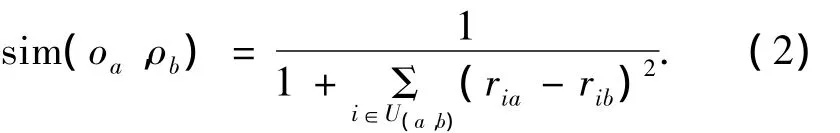
1.1.2 条件概率法

将资源相似程度看作是在某一资源受到指定用户评价的条件下，另一资源也同时受到该用户评价的概率p(oa|ob).如果令Freq(oa)和Freq(oa，ob)分别表示资源oa的评价用户数和同时评价资源oa和ob的评价用户数，则条件概率法的计算过程表示为

1.1.3 皮尔森法

皮尔森法采用数理统计的思想，将资源评价看作是同一样本空间中，重复实验下的抽样结果.如果令r和r分别表示资源o和o资源所得到用ab户平均评分，U(a，b)定义同类欧式距离法，则皮尔森法的计算过程表示为

与其他相似度计算方法相比，皮尔森法具有最佳的线性逼近程度，能够应对“分数膨胀”和“分数贬值”问题.

实际中，采取何种资源相似度计算方法依赖于推荐系统评价数据集特征.

1.2 评价预测

评价预测(效用函数f)根据相似度计算结果，对与未知评价资源oj相似的所有资源进行评价值聚合运算，从而得到指定用户ui对oj的评价预测值.考虑到资源历史评价信息的时效特征，引入时效量化函数后的评价预测方法表示为

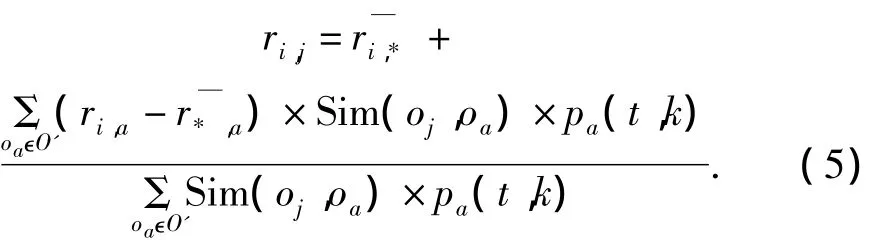
式中:O＇表示用户ui评价过且与oj相似的资源集合;r表示这|O＇|个资源的历史评价的平均值;pa(t，k)根据不同时间步t和控制参数k，量化oa历史评价的时效值;pa(t，k)是模型的研究重点.

2 资源时效量化方法

德国心理学家艾宾浩斯采取无意义音节作为材料，以重学法揭示遗忘过程中，记忆时效随时间变化特征，如图 1［11］所示.

在推荐系统中，指定资源的评价信息反映了用户对该资源的主观认可程度.这种主观认可程度必然随时间发生与遗忘过程类似的衰减情况.同时，根据记忆心理学研究成果，不同的记忆源存在遗忘衰减程度差异，用户感兴趣的记忆材料更容易被记牢.这与推荐系统中不同资源存在时效衰减差异的要求相同.基于此，将描述记忆特征的遗忘曲线作为衡量资源的时效变化基础，具有一定实际性和参考性.

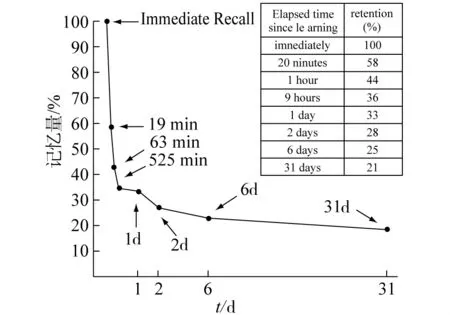
图1 遗忘过程遗忘曲线Fig.1 Time-utility Curve of forgetting procedure

本节首先获得遗忘曲线的基本量化函数，该函数体现出单个阶段内时效随时间变化趋势.然后，根据用户反馈，动态调整时效衰减程度，确定任意时刻拟合用户兴趣的多阶段时效量化方法.最后，设计时间单位映射函数.

2.1 单阶段时效量化方法

如果将当前时效发生体看成一个信息量储藏室，初始时效性作为该室的输入，则根据遗忘特征，资源历史评价信息的时效保持量为时间步t的函数pa(t，k)，其中k用于控制时效的遗忘速率，该过程如图2所示.

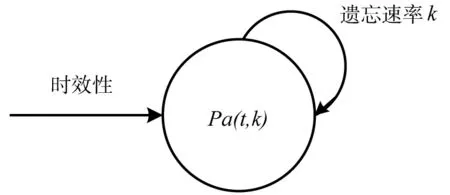
图2 记忆的一室模型Fig.2 One-compartment model of memory

将图2的动态过程转换为微分方程形式，表示为

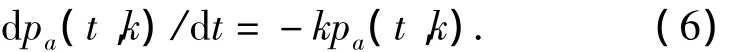
求解式(6)的原函数 pa(t，k)，表示为

式中:t∈(0，∞)，表示的遗忘曲线应取坐标系第一象限;p0为该曲线在y轴上的截距，即时效的初始值，由于被试材料的初始记忆时效值均从100%开始进行衰退，故取p0=1.

根据上述参数设定，资源oa的单阶段时效量化方法以式(8)为基础，根据当前时间步t及遗忘速率k获得资源历史评价信息的时效值.

式中:遗忘速率k是反映资源遗忘曲线衰减差异的主要参数.在后续内容中，将根据用户兴趣漂移，动态学习式(8)中k的数值，建立时效多阶段量化方法.

2.2 多阶段时效方法

本节根据忆心理学中记忆加强现象，将控制参数k的确定方法理解为多个阶段的遗忘曲线的调整过程.

针对同一被试资料，记忆加强是指经过学习，记忆出现阶跃(恢复完全记忆)并产生具有更低遗忘速率的新阶段遗忘过程.如果令t1、t2和t3分别表示发生3次重新学习的时间步，则遗忘曲线调整过程如图3所示.

图3 多阶段遗忘曲线调整Fig.3 Curve update in multiple procedures

图3可看作是由用户兴趣变化而导致的遗忘速率动态调整过程.如果令tn－1和tn为遗忘曲线发生记忆加强现象的任意相邻时间步，kn－1为遗忘曲线从tn－1到tn的遗忘速率，则对于资源oa，表示该遗忘阶段的时效量化函数表示为式中:还需进一步确定kn－1的学习策略.根据推荐系统的实际运行特征，将用户反馈作为刺激遗忘速率发生改变的基本因素.

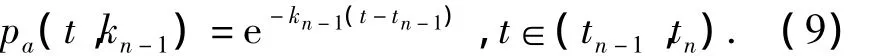
为便于分析相邻阶段遗忘曲线的调整方式，将遗忘速率调整后的新遗忘曲线向x轴反向平移，使之与原遗忘曲线具有共同起点.令调整前后的遗忘速率分别为kn－1和kn，则上述操作过程如图4所示.

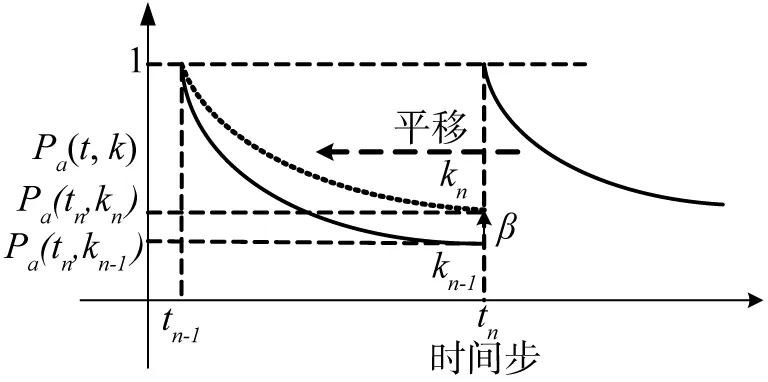
图4 时效遗忘速率调整分析Fig.4 Analysis of forgetting-ratio update

在图4中，根据用户评价反馈，发生曲线遗忘速率调整.若令β表明在时间步tn时新旧遗忘曲线的衰退差异，则根据式(9)，β的数值大小表示为

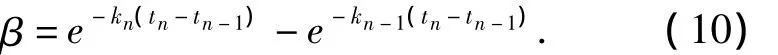
化简式(10)，由β建立kn－1和kn的数值关系，表示为

式中:(1－pa(tn，kn－1))为遗忘曲线在时间步tn时β取值的上限.为控制每次用户反馈对曲线的调整程度，将(1 －pa(tn，kn－1))划分为 δ个线段，调整程度β与时效保持程度的量化关系表示为

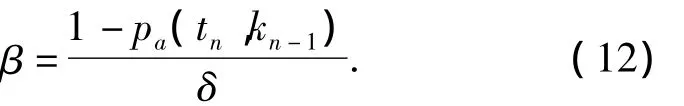
在推荐系统中，δ可设定为一个大于1的正整数.将式(12)代入式(10)，消去β，得到的kn的计算公式，表示为

式中:遗忘速率的调整过程呈现递归关系，如果令初始遗忘速率为k0，结合式(9)和式(13)，可确定资源历史评价信息在多阶段遗忘过程中任意时刻的时效量化函数，从而满足评价预测过程中相关要求.

2.3 时间单位映射函数

“时间步”是实际时间单位的一种离散化表示，常用于研究与时间特征耦合的系统中.在将系统付诸实践时，需根据系统应用背景，设计实际系统时间到时间步的时间单位映射函数.

考虑到不同时间单位在时效量化方面的等价性，设计线性函数将系统时间“毫秒”映射到FCCFRM所能够识别的时间步.时间单位映射函数的构造过程为

1)针对单阶段时效量化函数，当pa(t，k)∈(0，1］时，f需满足从系统时间 T:［0，∞)到时间步t:［0，∞)的一一映射，表示为

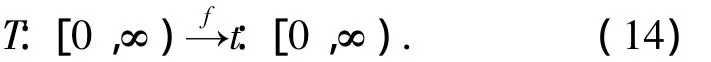
2)根据式(3)，当 pa(tϑ，k)=0.1 时，表明当前时间步该评价记录已基本丧失推荐效用，如果时效继续下降，则对该记录的时效量化过程无任何实际意义.基于此，在式(3)中引入临界时间步 tϑ，表示为

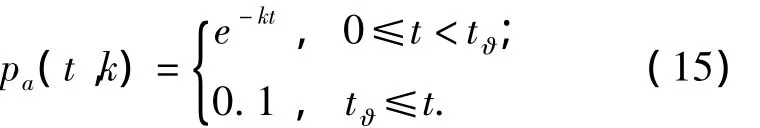
如果用Tϑ表示tϑ对应的临界系统时间，则结合式(15)，式(14)可进一步表示为

根据式(16)，单阶段时效量化方法的时间单位映射函数可表示为

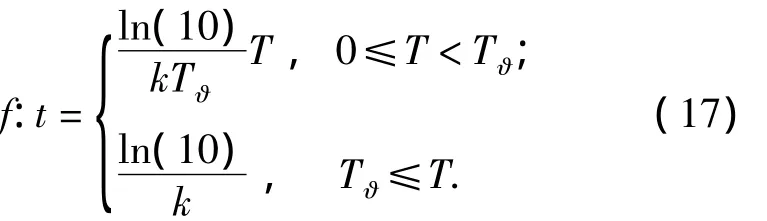
3)针对多阶段时效量化方法，将遗忘速率km代入式(15)求.根据线性函数的等价特性，利用式(17)已确定的函数形态求遗忘速率km下对应的，表示为

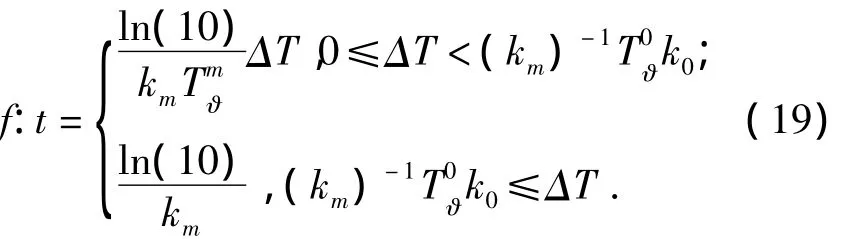
式中:k0表示初始遗忘速率，ΔT表示当前系统时间距上一次用户反馈的系统时间增量.

3 仿真分析

3.1 数据准备

将推荐系统中经典的数据集MovieLens［4］用于仿真分析.MovieLens由真实网络中71 567个用户对10 681个不同电影所进行的超过10 000 000条评价组成.每一条评价记录包括用户标识，电影标识，评价数值和时间戳.为验证FC-CFPM系统的推荐效果，取原始数据集中前10 000条时间相邻的资源历史评价信息为初始仿真数据集.采用交叉验证的方式将初始实验数据集分成训练集和测试集，划分百分比为0.2，即8 000条训练数据和2 000条测试数据.其中，训练集用于获取资源历史评价信息的遗忘速率，测试集将根据训练得到的时效分析结果进行评价预测.

测试过程采取增量学习的方法，其过程为:根据测试记录中资源标识，获取该资源的时效遗忘速率，并根据系统时间差，计算时效数值进行推荐.当推荐结束后，针对该记录反馈的资源进行遗忘速率的调整，同时，将评价预测后测试记录移入训练集的末尾，为后续推荐过程中计算资源间相似度提供基础.

平均绝对误差(mean absolute error，MAE)作为衡量FC-CFPM在不同实验中推荐效果，其计算方法如式(20)所示.其中，b(n)表示推荐系统计算得到的预测数值，bp(n)表示根据用户反馈得到的真实评价值.MAE体现推荐预测值与实际用户反馈值之间的平均差异.显然，MAE的值越小，说明推荐系统的评价预测效果越优秀.

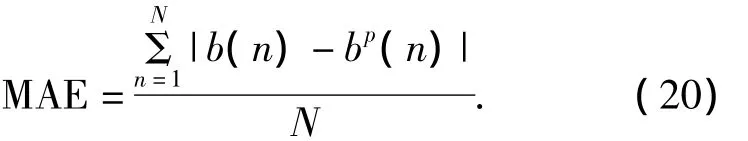
3.2 参数设定

表1 参数设定Table 1 Setting of parameters

k0的数值在仿真过程中会发生动态调整，仅需设定初值即可.

3.3 惰性因子δ取值分析

惰性因子δ用于控制遗忘速率调整程度.δ越大，用户评价反馈对该资源的时效遗忘速率更新效果越不明显.惰性因子δ的取值无法同其他系统参数一样，或通过计算训练集上相关统计特性获取，如初始临界时间，或通过训练过程动态调整.基于此，在惰性因子δ取10、20、50和100的基础上，运行FC-CFRM，根据MAE结果，确定δ的合理取值，仿真结果如图5所示.

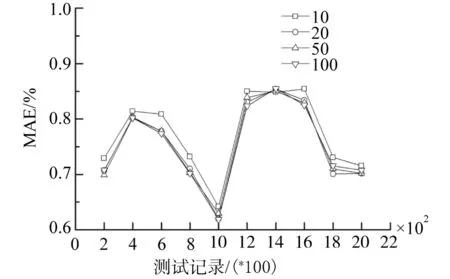
图5 δ取值对推荐效果影响Fig.5 Effects of various values ofδ on recommendation

图5中，每条曲线表示不同δ取值下FC-CFRM的10次分段MAE采样情况，分段长度为200.根据采样结果，FC-CFRM在不同测试记录分段上的MAE变化趋势相同，数值上呈现波动状态.

其中，δ=10的MAE数值仅在第1 200～1 400条测试记录上与其他实验结果相当(MAE=0.848 17)，在其他数据分段上，均具有较高的MAE值，表现为更差的推荐效果.

当δ=20、50、100时，MAE在不同数据分段下的差异最大值为0.014 8，位于δ=20和δ=100的第1 600～1 800条记录上，最小值为0.009，位于取20和50的曲线的第800～1 000条记录上，均值为0.000 312.对 δ=20、50、100 的 MAE 曲线采取线性拟合方式做相似度分析，其拟合后的直线基本吻合.

基于上述分析，当惰性因子δ取大于10的正整数时，FC-CFRM的推荐效果不因δ取值的改变而出现较大的波动.在后续试验中，采用δ=50.

3.4 推荐效果对比分析

推荐效果对比分析用于衡量不同模型在测试集上推荐效果.实验中所采取的对比方法包括:缺乏考虑资源历史评价信息时效性的经典协同过滤推荐模型(N-CFRM)［5］，采取简单指数k=1时效量化的协同过滤推荐模型(E-CFRM)，基于机械遗忘曲线时效量化的协同过滤推荐模型(F-CFRM)［14］，基于遗忘曲线的协同过滤推荐模型(FC-CFRM).推荐效果分析利用式(21)计算其他推荐模型*-CFRM与N-CFRM的MAE差异程度，若该值为负数，说明其推荐效果较N-CFRM更差.反之，若该值为正数且其值越大，则推荐效果越优.实验结果如图6所示.

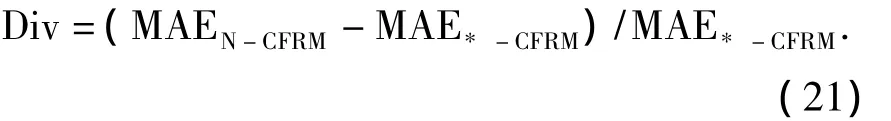
图6 推荐效果对比分析Fig.6 Comparison analysis of effect of recommendation

在图6中，每一分段中包含了3种推荐模型与N-CFRM的MAE差异程度，分段长度为200.总体上，所有推荐模型的推荐误差度在不同分段数据集上呈现出波动状态.其中，E-CFRM有7个正数分段，3个负数分段.F-CFRM有8个正数分段，2个负数分段.FC-CFRM全部为正数分段.针对每一种推荐模型，表明其具体推荐效果的MAE统计特征量如表2所示.

表2 MAE统计分析Table 2 Statistic analysis of MAE

根据表2，各推荐方法的平均推荐效果排序:E-CFRM＜N-CFRM＜F-CFRM＜FC-CFRM.稳定性排序:F-CFRM＜E-CFRM＜N-CFRM＜FC-CFRM.

由于E-CFRM采取人工方式设定指数函数的遗忘速率，忽略用户兴趣对不同资源在时效量化的影响，导致无论在推荐效果和推荐稳定性方面，均比N-CFRM表现更差.

从F-CFRM的实验结果上看，采取遗忘曲线能够较好的拟合资源时效随时间变化情况，表现为推荐平均效果较N-CFRM有所提高，但其忽略了资源时效量化存在多阶段遗忘过程的特征.在用户兴趣发生变化时，F-CFRM的推荐效果会出现较大波动，即推荐过程不可控现象.

基于上述分析:FC-CFRM能够采取合理的历史信息时效量化模型，跟踪用户兴趣变化，动态调整资源历史评价信息的时效遗忘速率，提供稳定且质量较高的推荐效果.

4 结束语

针对历史评价时效特征，提出一种用遗忘曲线协同过滤推荐模型.实验结果表明，与其他推荐模型相比，模型能够合理揭示遗忘速率随用户兴趣的变化规律并提供稳定且质量较高的推荐效果.

现有推荐系统将用户评价作为衡量资源效用的唯一标准，缺乏对环境等其他因素的考虑.当推荐对象为具体网络资源时，环境等因素往往更能够反映资源实际运行状态.在后续研究中，拟将时效量化与多属性评价相结合，设计具有时效特征的多属性协同过滤推荐系统.

［1］许海玲，吴潇，李晓东，等.互联网推荐系统比较研究［J］.软件学报，2009，20(2):350-356.XU Hailing，WU Xiao，LI Xiaodong，et al.Comparison study of internet recommendation system ［J］.Journal of Software，2009，20(2):350-356.

［2］董丽，刑春晓，王克宏.基于不同数据集的协同过滤算法评测［J］.清华大学学报:自然科学，2009，49(4):590-594.DONG Li，XING Chunxiao，WANG Kehong.Based on different data sets of evaluating collaborative filtering algorithms［J］.Journal of Tsinghua University，2009，49(4):590-594.

［3］FOLDBERG D，NICHLOSD，OKIB M，et al.Using collaborative filtering to weave an information tapestry［J］.Communications of ACM，1992，35(12):61-70.

［4］KONSTAN J A，MILLER B N，MALTZ D，et al.Grouplens:applying collaborative filtering to usenet news［J］.Communications of the ACM，1997，40(3):77-87.

［5］PARK S，PENNOCK D.Applying collaborative filtering techniques to movie search for better ranking and browsing［C］//Proceedings of the 13th Association for Computing Machinery Special Interest Group on Knowledge Discovery in Data.San Jose，California，USA，2007:550-559.

［6］孙超.基于Agent的推荐技术的研究与应用［D］.大连:大连海事大学，2009:35-37.SUN Chao.Research and application of recommendation technologies based on agent［D］.Dalian:Dalian Maritime University，2009:35-37.

［7］KOYCHEV I，SCHWAB I.Adaptation to drifting user’s interests［C］//Proceedings of ECML 2000 Workshop:Machine Learning in New Information Age.Barcelona，Spain，2000:39-46.

［8］KUKAR M，LJUBLJANA S.Drifting concepts as hidden factors in clinical studies［C］//Artificial Intelligence in Medicine 9th Conference on Artificial Intelligence in Medicine in Europe(AIME 2003).Protaras，Cyprus，2003:355-364.

［9］YIDing，XUE Li.Time weight collaborative filter［C］//Proceedings of the 14th ACM International Conference on Information and Knowledge Management CIKM’05.Bremen，German，2005:485-492.

［10］KATAKISG，TSOUMAKAS，VLAHAVAS I.An ensemble of classifiers for coping with recurring contexts in data streams［C］//Proceedings of the Conference on ECAI 2008:18th European Conference on Artificial Intelligence.Patras，Greece，2008:763-764.

［11］HERMANN E.Memory:a contribution to experimental psychology［EB/OL］.［2011-12-09］.http://psy.ed.asu.edu/～ classics/Ebbinghaus/index.htm.