非圆信号的四阶累积量测向新方法

刁鸣，安春莲，万文龙

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

在空间谱估计中，当入射信号为非圆信号时，阵列接收数据的椭圆协方差矩阵非零，因此在接收端可以同时对阵列的接收数据协方差矩阵和椭圆协方差矩阵进行处理，从而达到提高估计性能和扩展阵列孔径的目的.常见非圆信号有AM信号、MSK信号以及BPSK信号等，其在通信当中有广泛的应用，从而使得对非圆信号的DOA估计［1-4］具有现实意义.

现有的非圆信号测向方法主要基于MUSIC算法、ESPRIT算法和高阶累积量进行DOA估计.文献［5-6］研究了非圆信号测向的克拉美罗界，证明了非圆信号在DOA估计当中具有优势;文献［7-10］讨论了非圆信号的MUSIC算法和MUSIC-Like算法的估计性能和统计特性并说明了非圆信号测向算法的优良性能;文献［1］采用共轭 MUSIC算法进行DOA估计，能够扩展阵列孔径并且估计性能有所提高，但是阵列扩展能力较弱;文献［11］采用实数ES-PRIT算法测向，算法计算量小，但是会损失阵元;文献［12-15］采用高阶累积量进行估计，使得阵列扩展能力更强，但是扩展仍然不充分或者累积量矩阵当中存在较大的冗余数据，计算量较大.

在文献［13］的基础上，文章提出了一种基于四阶累积量的非圆信号测向新方法.该方法通过巧妙地构造累积量矩阵，使得阵列在四阶累积量的处理条件下得到了充分扩展，进一步提高了测向方法的阵列扩展能力，从而提高了测向方法的分辨率;同时，通过利用累积量矩阵之间的关系，避免了四阶累积量矩阵的重复计算，降低了算法的计算复杂度.最后，将本文提出的方法和MUSIC-Like方法以及文献［13］的 FO-EMUSIC方法进行实验仿真比较.

1 信号模型及阵列模型

1.1 非圆信号

对于一个信号s，当其满足 E［s］=0，且E［ss*］≠0时，称 s为圆信号;其他条件不变，当E［ss］≠0时，称s为非圆信号.非圆信号的非圆特性由非圆率ρ和非圆相位φ确定，其中ρ∈(0，1］，φ∈［0，2π)，本文只讨论ρ=1的情况，常见的BPSK信号.

在对阵列接收信号进行处理时，利用非圆信号E［ss］≠0这一特点，可以提高算法的估计精度和性能.非圆率为1的非圆信号可以由实信号经过移相得到，即

其中，φ为s的非圆相位，s0为一个实信号.

1.2 阵列模型

假设N个波长为λ的窄带远场独立非圆信号si(t)(i=1，…，N)分别从角度 θi(θiє［0，π］)入射到M元均匀线阵，阵元间距为λ/2.当阵列输出噪声均值为0、方差为加性高斯白噪声时，则在第t个快拍时刻阵列接收信号为

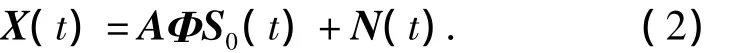
其中:

式中:xi(t)和ni(t)分别表示第t个快拍时刻第i个阵元上的接收数据和噪声数据;φi为第i个信号的非圆相位，S0(t)为实信号;A为阵列导向矢量矩阵，且 ui=e－j2πdcosθi/λ，d= λ/2.

2 新方法测向原理

2.1 MUSIC-Like方法和FO-EMUSIC方法

为了书写方便，在下文中不引起混淆的地方将表达式中的时间t去掉.利用四阶累积量阵列扩展特性的MUSIC-Like方法可以通过构造接收数据矩阵R1实现，其第(k1－1)M+k2行、第(k3－1)M+k4列的元素为 cum(xk1，，，xk4)，其中，cum(·)表示求·的四阶累积量，k1、k2、k3、k4є{1，2，…，M}，则

其中，ξi=cum(s0i，，，s0i)为正实数.显然，矩阵R1是一个M2×M2维的矩阵，但是其实际扩展后的等效阵元数目为2M－1，因此矩阵R1中有大量的冗余数据，使得算法的计算复杂度大大增加.

利用四阶累积量性质和非圆特性的FO-EMUSIC方法所构造的四阶累积量矩阵为

其中，R2和R3第(k1－1)M+k2行、第(k3－1)M+k列的元素分别可以表示为 cum(x，，xk3，xk4)，cum(，，xk3，xk4)，则

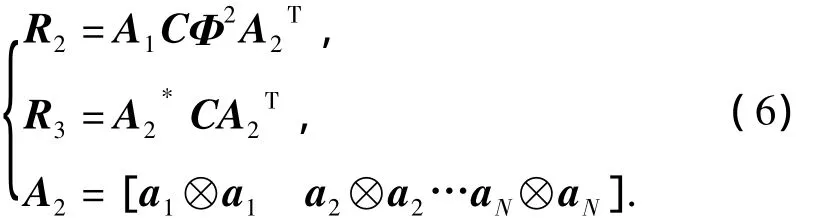
显然，矩阵R0是一个2M2×M2的矩阵，对于均匀线阵，经过去冗余处理过后R0可降维到4M×4M，其扩展后的阵元数为3M－2.FO-EMUSIC方法相对于MUSIC-Like方法进一步提高了阵列扩展能力并降低了算法的计算量，但其阵列扩展性能并没有得到充分的发挥，并且计算量可以进一步的降低.

2.2 非圆测向新方法

在上述2种方法的基础上，为了减少四阶累积量矩阵中的冗余数据并充分扩展阵列孔径，提出了一种阵列扩展能力更强、计算量更小的非圆信号四阶累积量测向方法.所提方法充分利用均匀线阵列的数据结构特点和信号的非圆特性直接构造维数较低的数据协方差矩阵.为了后续公式表示方便，记a0i=［1］T，B1=［b1(θ1)b1(θ2)…b1(θN)］，B2=，其中

构造累积量矩阵Rn1和Rn2，其第(k1－1)M+k2行、第(k3－1)M+k4列的元素取值分别可以表示为cum ()和 cum()，其中k1，k3є{1，2}，k2，k4є{1，2，…，M}.当 k1和 k3取值为1时，xk1和xk2取值为x1;当 k1和k3取值为2时，xk1和xk2取值为xM.则:

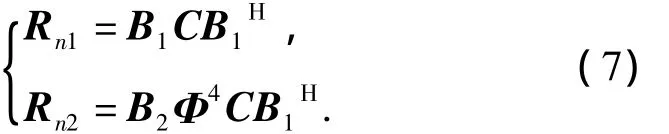
由于矩阵C为实对角阵，且B2=，有=构造所提方法的四阶累积量矩阵如下:

对R进行奇异值分解:

式中:UN为由小特征值对应的特征矢量所构成的噪声子空间，且.由于阵列流型矩阵与信号子空间张成同一空间，根据信号子空间与噪声子空间的正交性可得

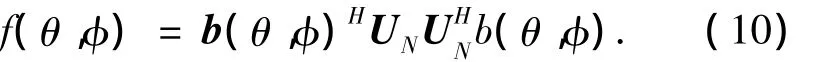
当式(11)取负号时，式(10)的值取最小，则本文所提方法的空间谱函数可以表示为

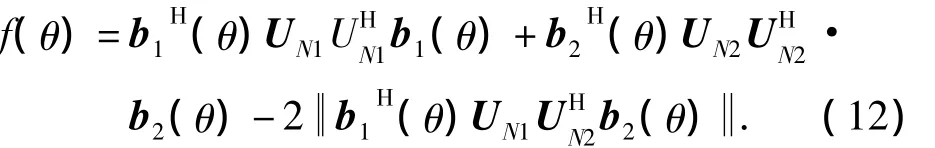
本文提出方法步骤如下:

1)由阵列接收信号求出2个累积量矩阵Rn1和Rn2，并按照公式(8)构造数据矩阵R;

2)对R进行奇异值分解，得到小特征值对应的噪声子空间，进而得到UN1和UN2;

3)根据式(12)采用MUSIC算法进行谱峰搜索，空间谱曲线中极小值点对应的位置即信号的波达方向估计.

2.3 计算量分析

由文献［13］知，计算一个四阶累积量需要9L次复乘运算，其中L表示快拍数，奇异值分解的计算量约为O()，其中M0表示所构造的累积量数据矩阵的维数.由此可知，MISIC-Like方法的计算量为9M4L+O(M6)，去冗余的FO-EMUSIC方法的计算量为108M2L+O(64M3).

由式(7)可知，Rn1=，因此在计算Rn1时可以只计算其上三角矩阵中的累积量，然后根据共轭对称性即可获得其下三角矩阵位置处的累积量值;此外，Rn1和Rn2中第M行和第M+1行相同，存在冗余，因而计算一行即可，从而可以进一步降低计算量.综上所述，本文所提出的测向方法的计算量为54M2L－9(2M－1)L+O(64M3).为了精确地估计出四阶累积量的值，通常L取值很大，有L≫M，因而文中所提的方法在计算量上近似为文献［13］中FOEMUSIC方法的一半.

3 计算机仿真及结果分析

为了验证本文提出方法的有效性，将本文方法与MUSIC-Like方法和FO-EMUSIC方法进行实验仿真并给出实验结果.实验仿真中采用的非圆信号为BPSK信号，采用阵元数为3的均匀线阵，当所估计角度与真实角度差的绝对值小于1°时，认为估计成功.均方根误差的计算采用

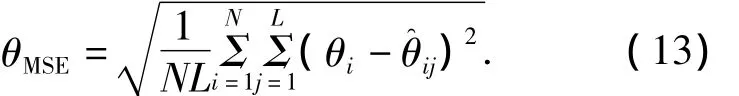
仿真1 取快拍数为2 000，信噪比为20 dB，8个远场窄带独立非圆信号，非圆相位均为0，分别从角度 25°、55°、65°、80°、100°、120°、140°、160°入射到三阵元的均匀线阵上.图1为本文所提方法进行10次DOA估计的空间谱曲线.

从图1可以看出，本文所提出的方法能够有效的对阵列孔径进行扩展，阵列扩展后的等效阵元个数为9，最多可以估计8个信号，而在相同条件下，文献［13］中的FO-EMUSIC方法最多只能估计6个信号.可见本文所提方法具有更好的阵列扩展能力.

图1 本文方法空间谱估计曲线Fig.1 Spectrum of the proposed method

仿真2 2个远场窄带独立非圆信号分别从86°和94°入射到3阵元的均匀线阵.取快拍数为2 000，进行500次独立实验，对本文方法、MUSIC-Like方法和FO-EMUSIC方法在不同信噪比时的估计性能进行仿真比较，得到3种方法的估计均方根误差和估计成功概率随信噪比变化的曲线如图2所示.

图2 估计性能随信噪比变化曲线Fig.2 Performance of estimation via SNR

在小信噪比时，由于MUSIC-Like方法和 FOEMUSIC方法有时只能搜索出一个信号，此时认为估计失败，按搜索的两个角度一样来计算估计均方根误差.从图2中可以看出，本文提出的方法在小信噪比时具有更小的估计均方根误差和更高的估计成功概率.由于该方法具有更好的阵列扩展能力，扩展后的等效阵元数更大，因此其估计性能优于MUSIC-Like方法和FO-EMUSIC方法，且较为有效地改善了测向方法在小信噪比时的估计性能.

仿真3 2个远场窄带独立非圆信号，其入射角度分别为 60°和(60+ α)°.取快拍数为 2 000，信噪比为10 dB，进行500次独立实验，将本文方法、MUSIC-Like方法和FO-EMUSIC方法在不同α时的估计性能进行仿真比较，得到3种方法的分辨力性能比较曲线如图3所示.

图3 3种方法的分辨能力比较Fig.3 Resolution of the three methods

在信号角度间隔较小时，由于3种方法有时只能搜索出一个信号，此时认为估计失败，按搜索的2个角度一样来计算估计均方根误差.从图3可以看出，本文提出的方法相对具有更高的估计成功概率和更小的估计均方根误差.由于本文方法扩展阵列后的等效阵元数较大，在其他条件相同的情况下，其分辨能力明显优于MUSIC-Like方法和FOEMUSIC方法.

4 结束语

本文提出了一种非圆信号的四阶累积量测向新方法，该方法充分利用阵列的结构特性和信号的非圆特性实现了阵列孔径的充分扩展，使得其阵列扩展性能优于FO-EMUSIC方法.在阵元个数相同的条件下，本文方法可以估计更多的信号个数，而且具有更好的估计性能.此外，通过利用累积量矩阵的结构特点，巧妙的降低了计算量，使所提方法在计算复杂度上相对其他基于四阶累积量的测向方法大大降低.理论分析和实验仿真验证了该方法具有计算量小，估计性能优良以及分辨力高等优良性能.

［1］SALAMEH A，TAYEM N.Conjugate music for non-circular sources［C］//Proceeding of the 2006 IEEE International Conference on Acoustic，Speech and Signal Processing.Toulouse，France，2006.

［2］CHEN Y H，LIN Y S.Forth-order cumulant matrices for DOA estimation［J］.IEE Proc on Radar，Sonar and Navigation，1994，141(3):144-148.

［3］GAO Feifei，NALLANATHAN A，WANG Yide.Improved MUSIC under the coexistence of both circular and noncircular sources［J］.IEEE Trans on Signal Processing，2008，56(7):3033-3038.

［4］SALAMEH A，TAYEM N.Angle of arrival estimation for non-circular signals［C］//2006 IEEE Sarnoff Symposium，Princeton，USA，2006.

［5］DELMAS J，ABEIDA H.Stochastic Crame＇r-Rao bound for noncircular signals with application to DOA estimation［J］.IEEE Trans on Signal Processing， 2004， 52(11):3192-3199.

［6］ABEIDA H，DELMAS J.Gaussian Cramer-Rao bound for direction estimation of noncircular signals in unknown noise fields［J］.IEEE Trans on Signal Processing，2005，53(12):4610-4618.

［7］DELMAS J.Asymptotically minimum variance second-order estimation for noncircular signals with application to DOA estimation［J］.IEEE Trans on Signal Processing，2004，52(5):1235-1241.

［8］HUANG Z T，LIU Z M，LIU J.Performance analysis of MUSIC for non-circular signals in the presence of mutual coupling［J］.IEEE Trans on Radar，Sonar ＆ Navigation，2010，4(5):703-711.

［9］ABEIDA H，DELMAS J.MUSIC-like estimation of direction of arrival for noncircular sources［J］.IEEE Trans on Signal Processing，2006，54(7):2678-2690.

［10］ABEIDA H，DELMAS J.Statistical performance of MUSIC-like algorithms in resolving noncircular sources［J］.IEEE Trans on Signal Processing， 2008， 56(9):4317-4329.

［11］郑春弟，冯大政，周祎，等.基于非圆信号的实值ESPRIT算法［J］.电子与信息学报，2008，30(1):130-133.ZHENG Chundi，FENG Dazheng，ZHOU Yi，et al.A real-value algorithm of ESPRIT via exploitation of non-circular sources property［J］.Journal of Electronics ＆ Information Technology，2008，30(1):130-133.

［12］LIU Jian，HUANG Zhitao，ZHOU Yiyu.A direction finding algorithm for noncircular signals based on higher－order cumulants［C］//2007 International Conference on Wireless Communications，Network and Mobile Computing.Changsha，China，2007.

［13］刘剑，黄知涛，周一宇.基于四阶累积量的非圆信号测向方法［J］.电子与信息学报，2008，30(4):876-880.LIU Jian，HUANG Zhitao，ZHOU Yiyu.A new forth-order direction finding algorithm for noncircular signals［J］.Journal of Electronics＆ Information Technology，2008，30(4):876-880.

［14］刘剑，于红旗，黄知涛，等.基于偶数阶累积量的非圆信号测向方法［J］.电子学报，2007，35(12):2371-2375.LIU Jian，YU Hongqi，HUANG Zhitao，et al.Direction finding algorithms for noncircular signals based on even order cumulants［J］.Acta Electronica Sinica，2007，35(12):2371-2375.

［15］DIAO Ming，CHEN Chao，YANG Lili.Propagator method for direction of arrival estimation based on an array extension of the fourth － order cumulant［J］.Journal of Harbin Engineering University，2010，31(5):652-656.