基于简化SIFT算法的无人机影像重叠度分析

邢诚

(武汉大学测绘学院，湖北武汉430079)

无人机超低空摄影是近几年来较热门的一个领域，它与传统数据采集方法相比具有以下几个优势［1-2］:1)机动快速的响应能力;2)平台构建、维护以及作业的成本极低;3)高分辨率图像和高精度定位数据获取能力，增强了后续处理的可靠性;4)无人机能够承担高风险或高科技的飞行任务;5)不必申请空域，国家对千米以下的空域不实行管制.由于上述的诸多优势，基于小型无人机平台搭建的对地观测系统已经成为世界各国争相研究的热点课题，现已逐步从研究开发阶段发展到实际应用阶段.

但是，无人机影像处理方面所遇到的问题是传统航空摄影测量所未遇见的，影像的处理归纳起来有以下几个问题［3］:1)影像的倾角过大且无规律、航向重叠度有时过小，灰度不一致，使得影像匹配难度大、精度低;2)无人机影像像幅小、数量多，造成工作量大、效率低，需研究高效的、自动化程度高的处理方法;3)飞行航线呈曲线，影像的旁向重叠度不规则、过小.所以，在影像处理工作进行之前，数据预处理——即图像可用性分析工作就显得尤为重要.去除不符合要求的图像，然后对需要补测的区域进行补摄.

序列影像重叠度分析工作是建立在稳定、高效的图像特征提取和匹配基础之上的，所以需要利用稳定性好、效率高的特征提取、匹配算法进行处理.D.G.Lowe在2004年总结了现有的基于不变量技术的特征检测方法，并提出了基于尺度空间的、对图像缩放、旋转甚至仿射变换均保持不变性的图像局部特征描述算子——SIFT(scale invariant feature transform)算子［4］.但传统 SIFT算法复杂度高、图像处理时间长，导致工作效率降低.本文提出一种简化的SIFT算法对无人机影像进行处理，并通过实验与传统SIFT算法做出了对比.

1 SIFT算法及改进

1.1 SIFT 算法

SIFT算法不仅具有尺度、旋转、仿射、视角、光照不变性，对目标的运动、遮挡、噪声等因素也保持较好的稳定性.该算法主要分为以下几个步骤:

1)建立尺度空间.利用不同尺度的高斯差分核与图像进行卷积生成高斯差分尺度空间［5-6］.

2)尺度空间极值检测及精确定位极值点.为了寻找尺度空间的极值点，每一个采样点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小，即将当前检测点与跟它同尺度的8个相邻点以及上下相邻尺度对应的9×2个点(共计26个点)进行比较，以确保在尺度空间和二维图像空间都检测到极值点.

通过拟和三元二次函数精确确定关键点的位置和尺度［7］(达到亚像素精度)，同时去除低对比度的关键点和不稳定边缘响应点，以增强匹配稳定性、提高抗噪能力.

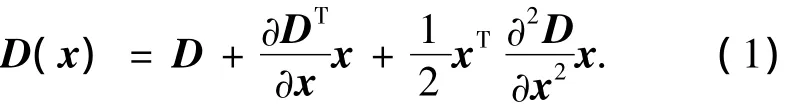
式中:x=(Δx，Δy，Δσ)T为采样点的位置及尺度的改正数.

3)关键点方向分配.利用关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数，使算子具备旋转不变性.

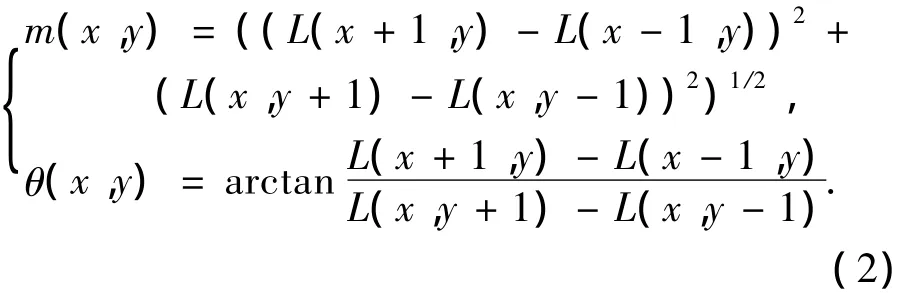
式(2)为计算像点坐标为(x，y)的像素点的梯度大小及方向的公式.其中，所采用的尺度为当前关键点所在的尺度.

在实际计算时，在以关键点为中心的邻域窗口内采样，并用直方图统计邻域像素的梯度方向.直方图的峰值代表了该关键点处邻域梯度的主方向，作为该关键点的方向.在梯度方向直方图中，当存在另一个相当于主峰值80%能量的峰值时，则将这个方向认为是该关键点的辅方向.一个关键点可能会被指定具有多个方向(一个主方向，一个以上辅方向).

4)特征点描述子生成.将坐标轴旋转为关键点的方向，以确保旋转不变性.对每个关键点使用4×4共16个种子点来描述，这样对于一个关键点就可以产生128个数据，即最终形成128维的SIFT特征向量.此时SIFT特征向量已经去除了尺度变化、旋转等几何变形因素的影响，再继续将特征向量的长度归一化，则可以进一步去除光照变化影响.

5)特征匹配.利用关键点特征向量的欧式距离作为2幅图像中关键点的相似性判定度量:

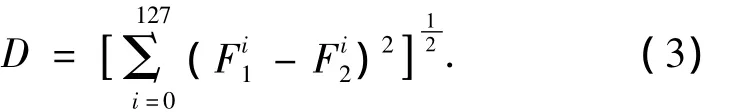
取基准图像中的某个关键点，并找出其与待匹配图像中欧式距离最近的前2个关键点，在这2个关键点中，如果最近的距离除以次近的距离小于某个比例阈值，则接受这一对匹配点.

1.2 算法改进

传统SIFT算法参数较多，算法复杂度高，导致处理过程时间很长，所以对于匹配精度要求不高但实时性要求高的任务，可以考虑采用简化的SIFT算法进行处理，以缩短图像处理时间.表1中列出的是用SIFT算法对一幅分辨率为768×576的图像进行处理，每一步骤所需时间，以及对多幅影像进行处理统计得到的每一步骤占总时间的百分比.

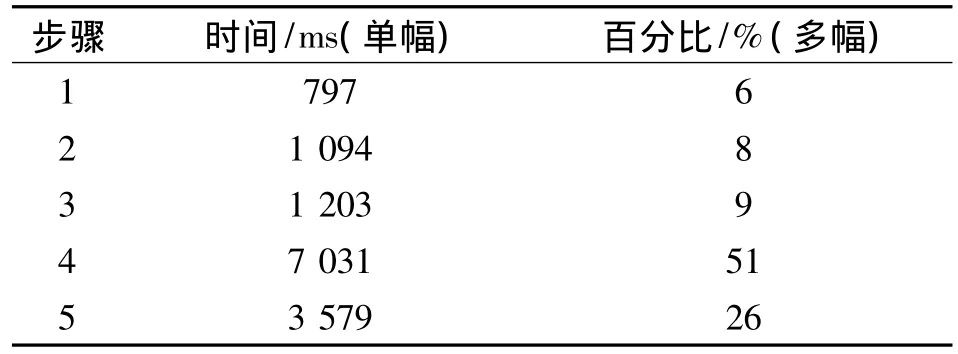
表1 SIFT算法各步骤耗时统计Table 1 Time consuming of each step in the SIFT

1.2.1 简化的SIFT算法

由表1中的统计数据可以看出，在传统SIFT算法中，生成特征向量和特征匹配2步骤占据了大部分时间，因此可以对这2个过程进行简化，以缩短处理时间.

首先是解决重复匹配问题.由于在原算法第3步过程中，将相当于主峰值80%能量的方向当作当前关键点的辅方向，这样就增加了特征点的数量，而且这些方向被指定为辅方向的特征点和具有主方向特征点的坐标是一样的，这会导致匹配结果发生重复的现象，同时也增加了计算时间.所以，在改进的算法中不考虑辅方向.

其次，原算法生成的128维特征向量占用时间长，主要是因为在关键点方向分配和生成特征向量2个步骤中都进行了关键点邻域直方图统计，所以在改进算法中考虑将这2步进行简化.首先按原算法第3步计算关键点主方向，高斯加权参数选择为当前关键点尺度(σ)的1.5倍，即1.5σ，统计 n个方向直方图，得到直方图统计量 H={h1，h2，h3，…，hn}，计算H中的最大值Hmax并设置为当前关键点的方向.寻找到关键点主方向的同时，为了加快描述子生成步骤的速度，需要记录下各像素点梯度信息.然后将关键点方向旋转至主方向，确保旋转不变性.生成描述算子时，关键点邻域窗口选择16×16窗口，高斯加权参数选择为特征描述向量窗口宽度的一半，统计关键点邻域n个方向的梯度信息(如图1所示)，由此可生成n维特征描述向量，即F={f1，f2，…，fn}.为了去除光照变化的影像，将特征向量进行归一化处理，即

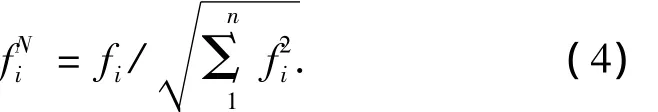
式中:fN表示归一化向量，i∈［1，n］.

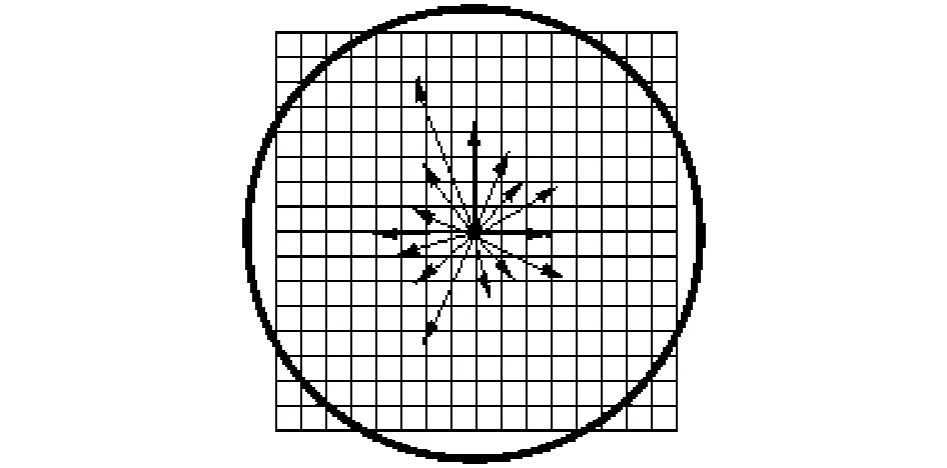
图1 特征向量统计窗口Fig.1 Statistics of feature vectors

1.2.2 特征向量方向数

通过对不同情况下大量影像对进行匹配实验发现，简化的SIFT算法对缩放、平移等基本图像变化可保持较好的稳定性，但对旋转或投影变换匹配成功率下降，所以特征方向数量的确定应以投影变换为参考进行设定.图2、3是分别对20组垂直旋转影像对和20组投影变换关系的影像对进行统计得到的结果.由统计结果可以看出当方向数确定为24的时候可以得到较稳定的匹配结果.在各组实验中，当特征向量方向数取为24时，均可以得到最高的匹配正确率，所以可以将特征向量方向数确定为24.

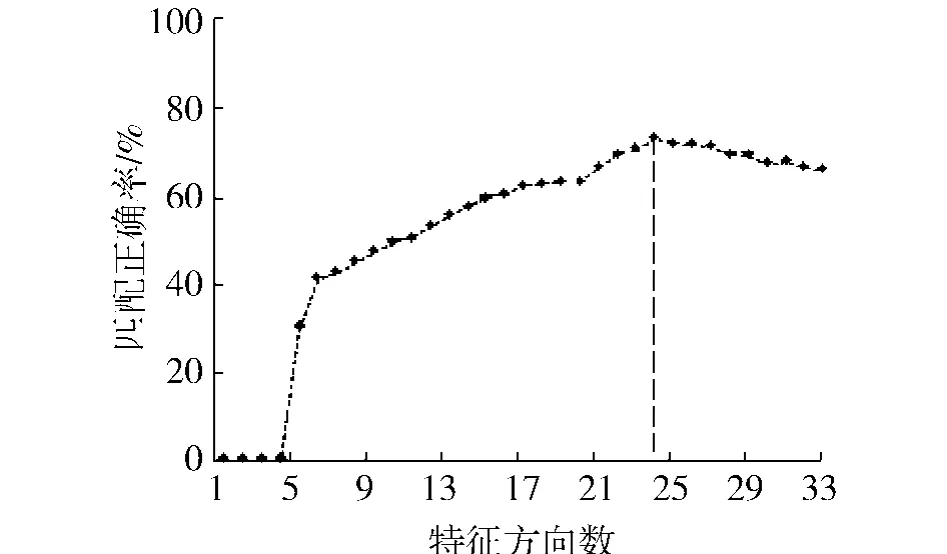
图2 方向数与匹配正确率统计结果(影像旋转90°)Fig.2 The statistics results of the number of the directions and the correctness(rotation with 90°)

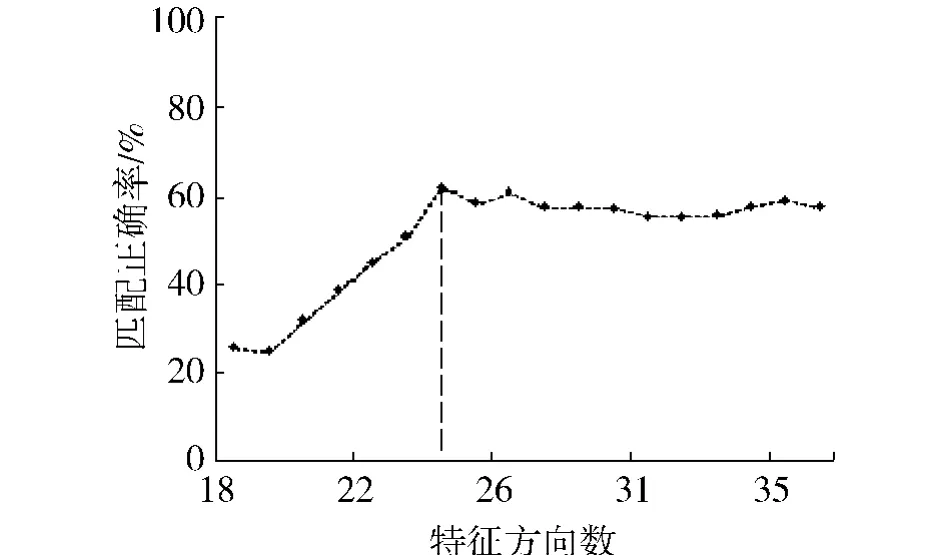
图3 方向数与匹配正确率统计结果(投影变换)Fig.3 The statistics results of the number of the directions and the correctness(perspective projection)

1.2.3 剔除误匹配点

由于对SIFT算法进行了简化，特征点的稳定性有所降低，导致匹配结果中误匹配点过多，所以需要对误匹配点进行剔除.这里可以采用RANSAC算法［8］对匹配点进行处理，获取正确的匹配点.实验表明，通过结合RANSAC算法处理，可以成功剔除误匹配点，得到正确的匹配点，在一定程度上弥补了简化算法的不足.

在经过RANSAC算法处理后，会删除较多的误匹配点，与原算法结合RANSAC算法处理后的结果相比，剩余的匹配点数量会有所减少，但对于高分辨率无人机影像来说，剩余的匹配点的数量通常可以满足后续图像处理的要求.简化算法中，关键点的数量和位置与原算法相同，只是在匹配后删除了更多的关键点，但是并不影像匹配的精度.

2 影像重叠度分析

2.1 影像重叠度

航摄像片不仅要覆盖整个测区，还要求像片间有一定的重叠度［9］.一般要求航向重叠度在60% ～65%，不得小于53%;旁向重叠度在30% ～40%，不得小于15%［10］.由于无人机稳定程度不如有人驾驶飞机，不易操纵，易受高空风力影响，会导致航线漂移，飞行的轨迹不再像传统的航空摄影沿直线飞行(航线弯曲度≤3%)，而呈曲线轨迹.这样使得拍摄影像的航向重叠度和旁向重叠度都不够规则.所以，首先对所获取的影像重叠度进行分析是十分必要的.

2.2 影像重叠度计算方法

影像重叠度的计算结果可以采用直方图统计的方式来记录，即将重叠度按10%一个柱进行统计，检验占匹配点数比例最大的柱代表的重叠度范围，以确定是否满足航向重叠度和旁向重叠度的要求(本文以计算航向重叠度为例).重叠度计算示意图如图4所示，箭头代表航线方向，阴影区域为重叠区.在飞行条件较好的情况下，航线弯曲度很小，所以在计算航向重叠度的时候可以不考虑相邻相片在y方向上的重叠度，按式(5)计算重叠度;在飞行条件较差的情况下，航线弯曲度可能会偏大，导致航向上相邻像对在y方向上重叠度较小，这会对后续数据处理造成影响，所以此时应以重叠面积来计算重叠度，式(6)为该种情况下重叠度计算公式.

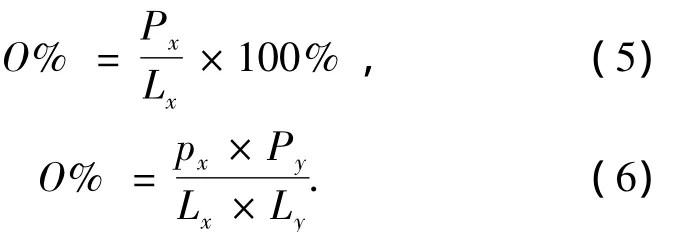
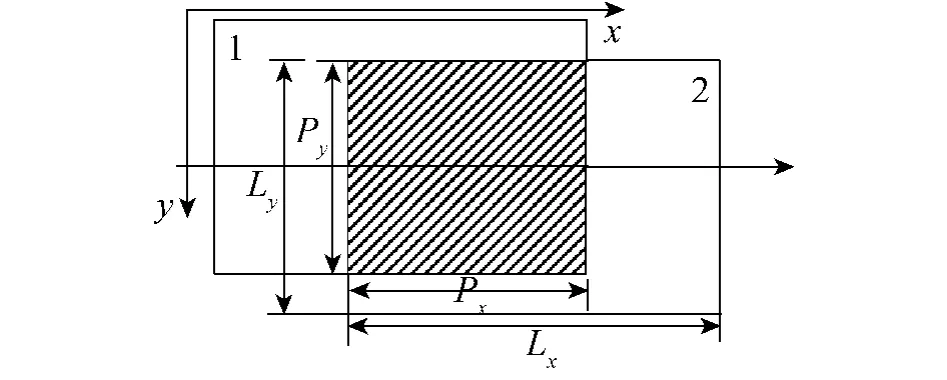
图4 像片重叠度计算示意Fig.4 The example for computing the overlapping degree

2.3 影像重叠度分析步骤

影像重叠度分析大致可以分为以下几个步骤:

1)采用简化的SIFT算法对序列影像中各幅影像进行处理，提取特征描述向量;

2)对提取的特征点集进行特征匹配;

3)用RANSAC算法对匹配结果进行提纯;

4)计算航向及旁向方向上相邻影像间的重叠度;

根据测图要求设定影像重叠度阈值，判断影像是否满足重叠度要求，对于不满足重叠度要求影像予以舍弃，对相应的区域要进行补测.

3 实验及结果分析

3.1 实验1

实验1主要对简化的SIFT算法与原算法做出了对比，处理结果如图5所示.图5第1列结果为简化的SIFT处理结果，第2列为原SIFT算法处理结果，第3列是简化SIFT结合RANSAC的处理结果;第1行影像间关系为任意旋转，第2行影像间关系为缩放，第3行影像间关系为投影变换;匹配正确率及处理时间如表2所示.

表2 实验1各行影像匹配正确率及处理时间统计Table 2 The correctness and time consuming results of the images in each row in Test 1

3.2 实验2

首先采用简化的SIFT算法对2幅分辨率为1 280×1 920的相邻影像进行特征提取及匹配，利用这些匹配点对两幅影像的重叠度进行计算，结果如表3所示，然后用RANSAC算法对匹配点进行提纯，除去误匹配点，利用提纯后的这些同名点对两幅图像的重叠度进行计算，统计结果如表4所示.利用简化SIFT与原SIFT分别对单航带序列影像(10幅影像)进行重叠度的计算以及计算时间统计的对比结果如表5所示.

表3 重叠度计算结果统计(含误匹配点)Table 3 The results of overlapping degree(outliers included)

表4 重叠度计算结果统计(误匹配点已除去)Table 4 The results of overlapping degree(outliers removed)

表5 单航带重叠度计算统计结果Table 5 The results of overlapping degree within a single flight strip

3.2 实验结果分析

通过实验1可以看出，简化的SIFT算法与原SIFT算法相比，匹配结果中误匹配点数量增多，匹配正确率下降，尤其对于投影变换关系的影像匹配成功率不高，但处理时间大大减少;在结合RANSAC算法进行处理后，误匹配点可以被成功剔除，从而得到正确匹配结果，这样在处理时间上与原SIFT方法相比就更有优势.

通过实验2可以看出:在未经RANSAC算法进行处理前，如表3所示，根据得到的匹配结果计算得到的重叠度结果存在一定的错误，在多个统计区间都会得到计算结果;经过RANSAC算法处理后，如表4所示，删除了误匹配点，利用正确的匹配点计算得到的重叠度结果趋于一致，都集中在61% ～70%，得到了正确的重叠度计算结果.

在表5的统计结果中，简化SIFT所得到的结果是先经过RANSAC算法进行过误匹配点剔除的，原SIFT算法的匹配结果同样也经过了RANSAC算法进行处理.利用提纯后的匹配结果对重叠度进行计算，简化算法和原算法可以得到完全一致的计算结果.

通过与原SIFT算法计算时间进行对比，说明简化的SIFT算法虽然在匹配成功率上较原SIFT算法有所下降，但处理时间有所减少，而且在结合RANSAC算法后，可以得到正确的匹配结果，与原SIFT算法的计算结果一致，这说明简化的SIFT算法提高了影像重叠度计算的效率.由于序列影像重叠度计算对匹配点的精度要求并不高，所以简化的SIFT很适合应用于重叠度计算，可以有效提高数据处理的效率.

4 结束语

本文首先介绍了一种简化的SIFT方法，将该方法与原SIFT方法做出了对比;其次对无人机序列影像的重叠度分析方法做出了说明，并将简化的SIFT算法结合RANSAC算法应用其中，通过实验证明了可行性.

［1］孙家炳.遥感原理与应用［M］.武汉:武汉大学出版社，2003:2-3.

［2］常庆瑞，蒋平安，周勇，等.遥感技术导论［M］.北京:科学出版社，2004:10-11.

［3］王聪华.无人飞行器低空遥感影像数据处理方法［D］.济南:山东科技大学，2006:5-6.WANG Conghua.Image data processing methods of UAV low-altitude remote sensing［D］.Jinan:Shandong University of Science and Tecnology，2006:5-6.

［4］LOWE D G.Object recognition from local scale-invariant features［C］//International Conference on Computer Vision.Corfu，1999:1150-1157.

［5］KOENDERINK JJ.The structure of images［J］.Biological Cybernetics，1984，50:363-396.

［6］LINDEBERG T.Detecting salientblob-like image structures and their scales with a scale-space primal sketch:amethod for focus-of-attention［J］.International Journal of Computer Vision，1993，11(3):283-318.

［7］BROWN M A.Multi-image matching using invariant features［D］.Vancouver:The University of British Columbia，2005:16-17.

［8］FISHCHLER M A.Random sample consensus:a paradigm for model fitting with application to image analysis and automated cartography［J］.Communication Association Machine，1981，24(6):381-395.

［9］李德仁，周月琴，金为铣.摄影测量与遥感概论［M］.北京:测绘出版社，2003:12-14.

［10］王佩军，徐亚明.摄影测量学［M］.武汉:武汉大学出版社，2007:16-1.