线性分布载荷作用下功能梯度简支梁弯曲解析解

李华东，梅志远，朱锡，张颖军

(海军工程大学船舶与动力学院，湖北武汉430033)

功能梯度材料(functionally graded materials，FGM)的概念是1984年，由日本材料学者平井敏雄等针对航天技术中出现的高落差温度(＞1 000℃)现象提出的［1］.其材料属性在剖面上连续变化，基本消除了宏观界面，FGM有效地实现了材料内部功能的渐变，达到了缓和热应力、避免或降低应力集中的目的［2］，同时，这种材料具有很好的可设计性，设计人员可以通过优化方法有目的地改变材料组成，以获得所期望的性能:减小最大挠度、增大基频或减小最大主应力［3］.FGM良好的物理性能和独特的设计思想引起了国际学术界和工程界的广泛关注，其在装甲防护、热力机械及人体医学等工程分支和系统内都得到了广泛的应用.

由于FGM是一种非均质材料，所以其材料基本物理性能的表述与均质材料不同，其结构的力学分析方法也不同于均质结构.用于FGM结构的主要理论分析方法［4］有:层合模型法、简化模型法与精确解法(解析法)，其中，解析法是严格求解问题的控制方程和边界条件，求出FGM结构的应力与应变分布的完全解析解.目前，对于功能梯度梁的求解能得到解析解的仅是极少数的情况.基于应力函数的半逆解法，于涛与仲政等［4-5］分别得出了均布载荷、端部集中力与力矩作用下的功能梯度悬臂梁的弯曲问题的解析解.Sankar等［6］假设梁的弹性模量在厚度上呈指数变化，得到了横向载荷作用下功能梯度梁的弹性解.而同样采用应力函数法，黄德进等［7］则将任意载荷利用正弦级数展开，得到了任意载荷作用下各向异性功能梯度梁的解析解和半解析解.

本文基于应力函数法，研究了线性分布载荷作用下材料属性在厚度方向上任意变化的功能梯度简支梁的弯曲问题，通过推导得到了适合线性载荷作用下功能梯度简支梁的更简洁的应力函数φ的表达形式，并给出了满足边界条件的各向应力应变和位移的显式解析表达式.

1 相容方程与平衡方程

1.1 载荷分布与材料属性假设

如图1所示，考虑一个矩形截面的简支梁，其深度为h，长度为l，体力忽略不计，在上表面承受线性分布载荷:

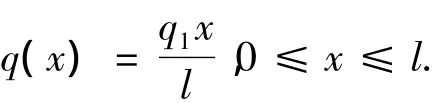
由于泊松比对功能梯度结构力学响应的影响较小［3］，假设其在整个结构上保持恒定于μ.材料的弹性模量只在厚度方向上发生变化，其分布采用如下函数进行表述:

式中:E1为上表层材料的弹性模量，E(z)为坐标z的任意函数.

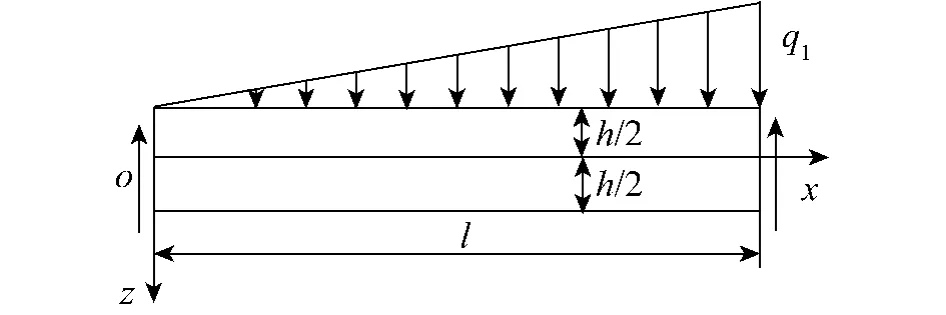
图1 功能梯度简支梁Fig.1 Simp ly supported functionally graded beam

1.2 基本微分方程

各应力与应变分量应满足以下平衡方程和相容方程［8］.

平衡微分方程:

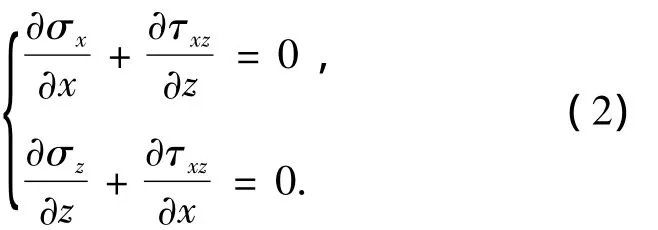
相容方程:

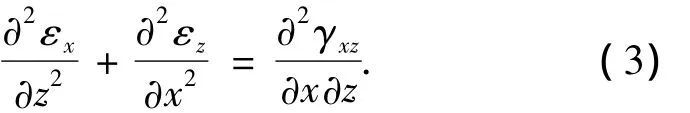
假设梁处于平面应力状态，采用平面应力本构关系，其通用表达式为

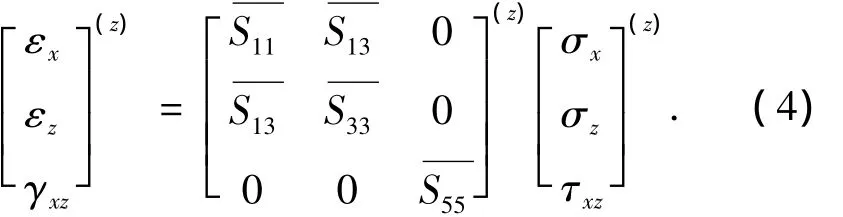
式中:

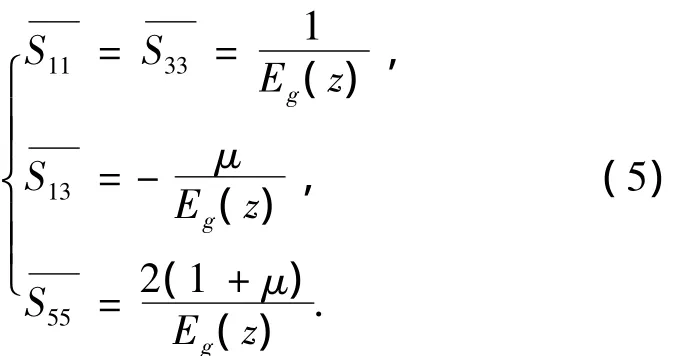
2 应力函数法求解

2.1 应力函数Φ

首先，引入以下形式的应力函数［10］Φ:

Φ与各应力满足以下关系式:

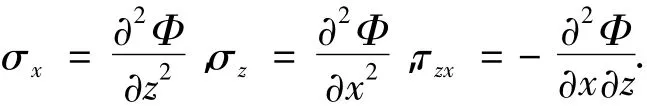
式中:φ0(z)、φ1(z)、φ2(z)与 φ3(z)均为待定函数，则可以得出各向应力的表达式为

从式(6)可以看到，φ0中的常数项与一次项、φ1中的常数项对应力没有影响，可以忽略.

2.2 边界条件

1)梁的上表面(z=-h/2):

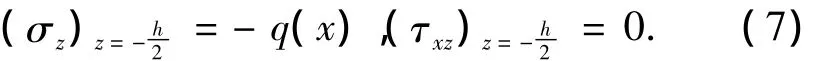
2)梁的下表面(z=h/2):

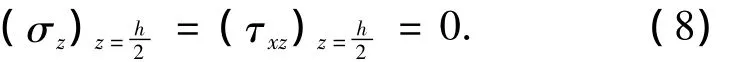
3)梁的两端:在梁的两端，根据圣维南原理，可以得出以下边界条件:σx在2个边界上均合成平衡力系，现在只给出x=l一端的，在后面将会发现其对于x=0处也是自然成立的，即

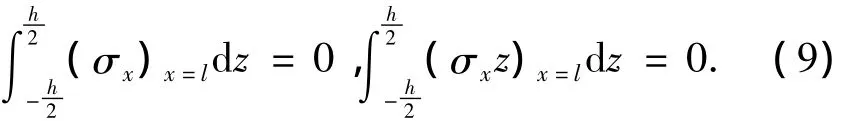
而切应力在梁的两端合成向上的反力:

4)位移边界条件:

将式(6)代入式(7)和(8)，得

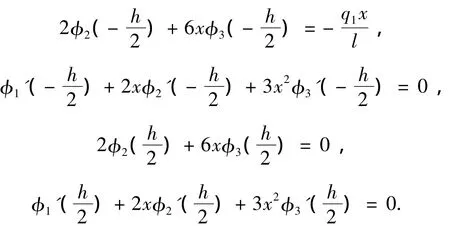
则可以得出:

2.3 平衡方程与求解

将式(4)和(6)代入相容方程式(3)，并合并化简得

式(14)对于任意x均是成立的，所以其系数和常数项必为0，最终得出4个平衡方程:

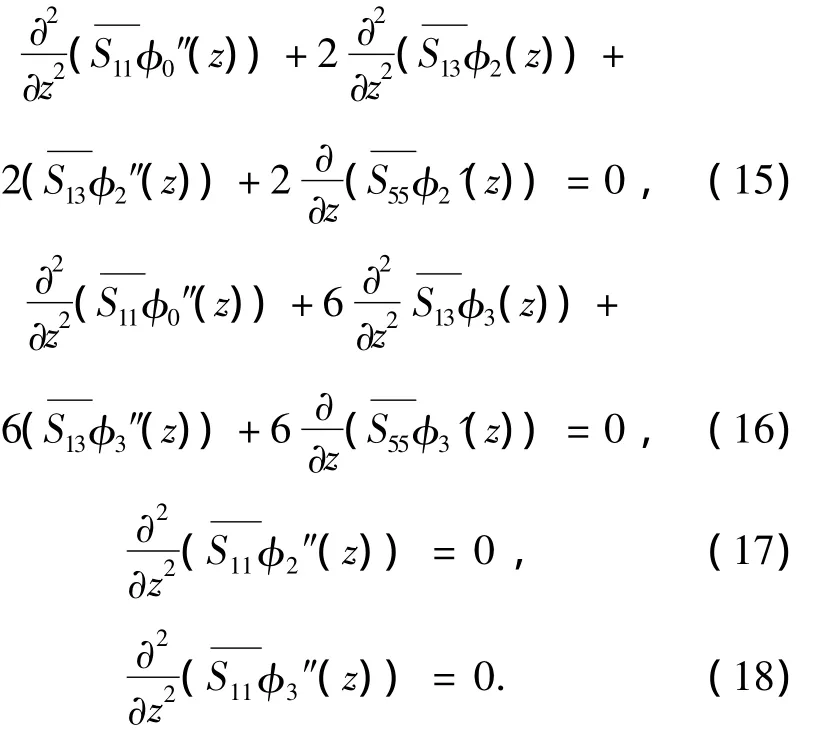
先求解式(17)，得

式中:I1(z)= ∫E(z)z d z，I12(z)= ∫I1d z，I0(z)=∫E(z)d z，I02(z)= ∫I0(z)d z.

由式(18)得

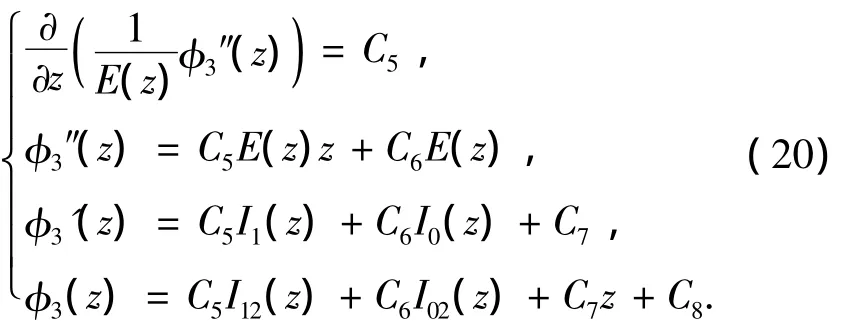
由式(16)得

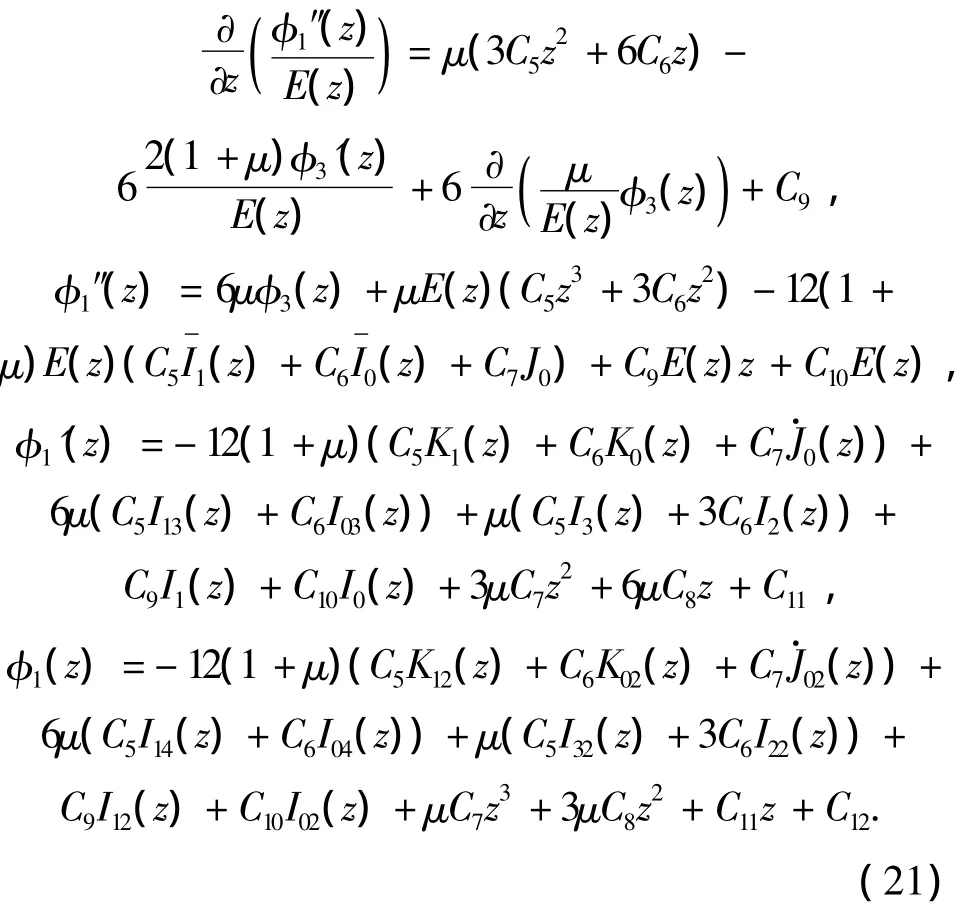
式中，因为φ1(z)的常数项对各应力分量的分布没有影响，所以可以设C12=0.各积分函数如下:

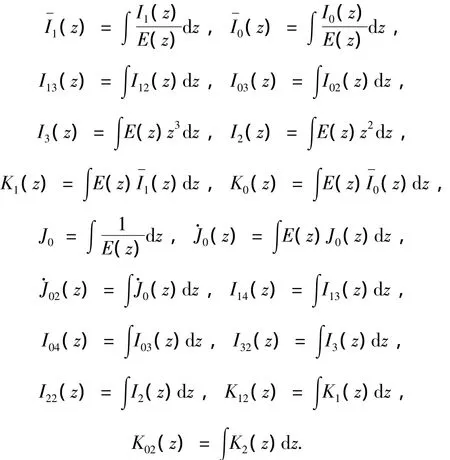
由式(15)得

式中，φ0(z)的一次项和常数项对各应力的分布没有影响，因而可以设C15=C16=0.

将式(19)代入式(12)所示的边界条件得

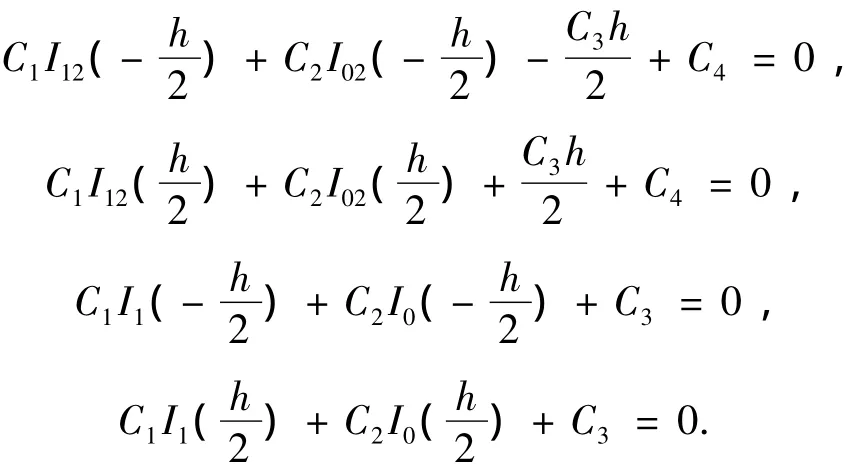
解之得

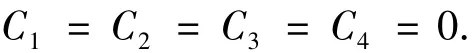
同样，将式(20)代入式(12)所示的边界条件，可以得出

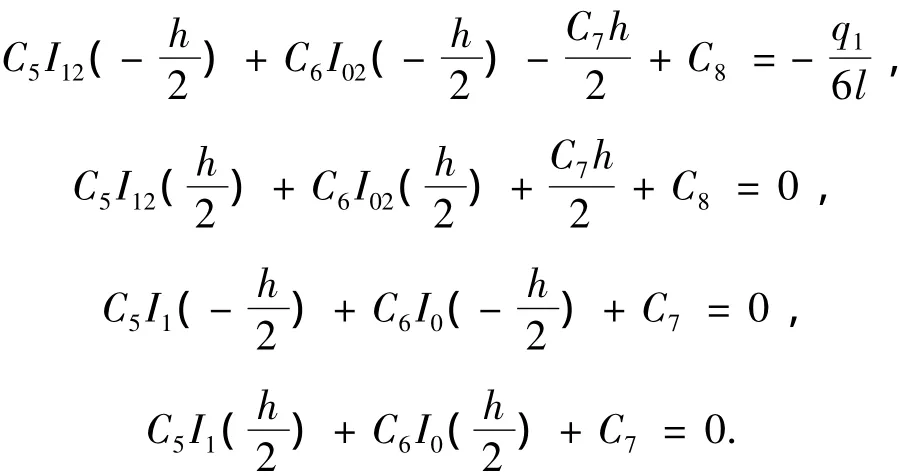
解之得

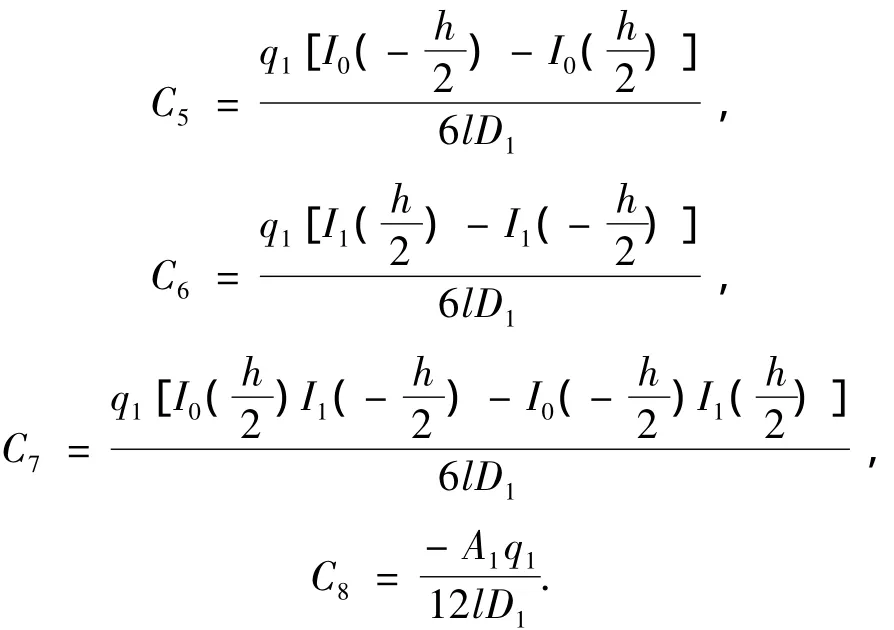
式中:

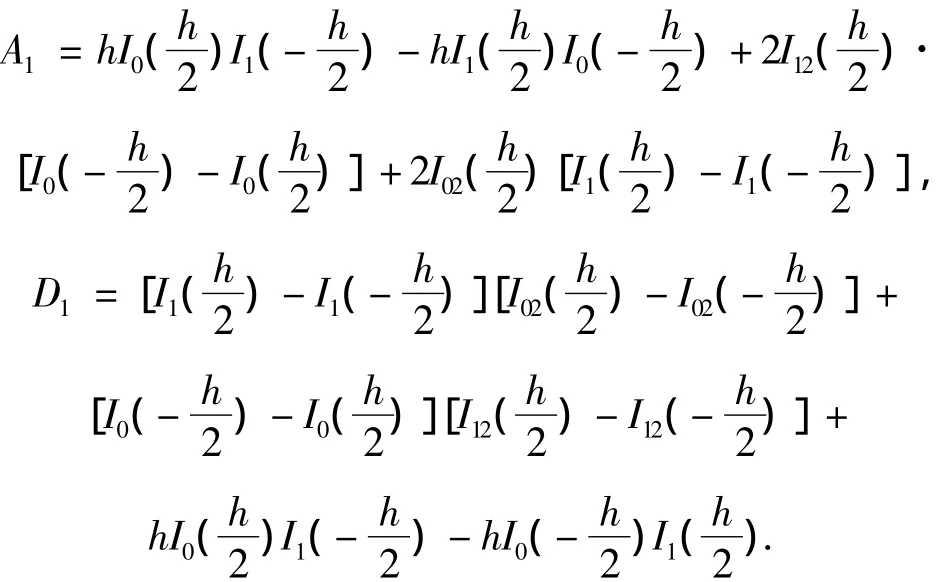
将式(21)代入式(12)、(13)中其满足的边界条件得

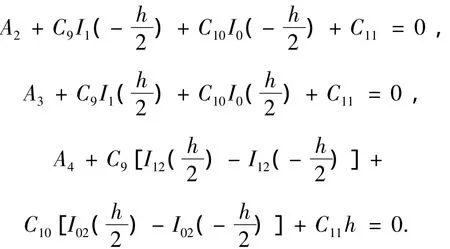
解之得

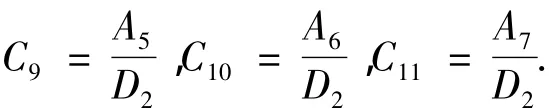
式中:

将式(22)代入式(13)中其所满足的边界条件得

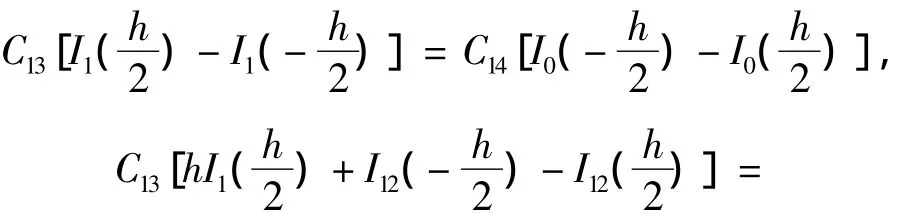
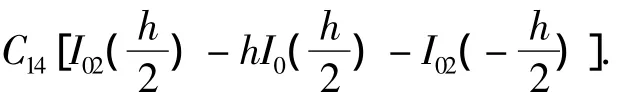
解之得

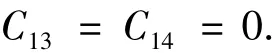
2.4 应力应变表达式

通过2.3节的求解，得出了参数Ci(i=1～16)的数值，可以得出φ0(z)=φ2(z)=0，而由式(6)可以得出σx在x=0处是为0的，所以在x=0处σx也会合成平衡力系，边界条件式(9)也是成立的.

同时可以得出，对于线性分布载荷作用下的功能梯度简支梁，可直接采用如式(23)所示的更为简洁的应力函数Φ进行求解.

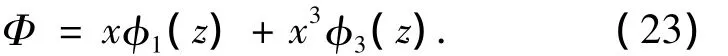
最终，得到各应力的表达式为

根据式(1)、(4)、(5)，即可得出各向应变的分布如下:

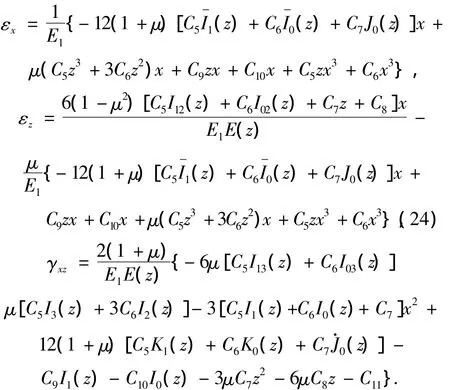
2.5 各向位移的求解

根据位移-应变的微分关系:

可以得出

式中:

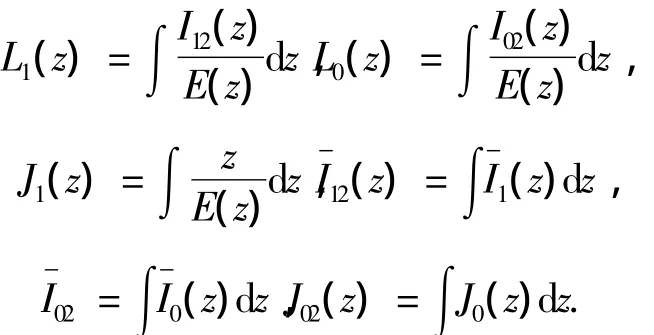
由式(24)及式(27)、(28)，得

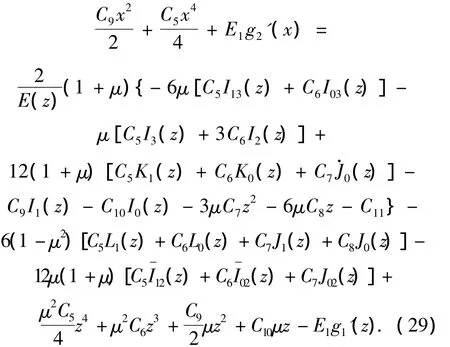
从式(29)可以看出，等式左边只是x的函数，等式右边只是z的函数，要使得两者相等，只有两边都等于同一常数a.于是可得

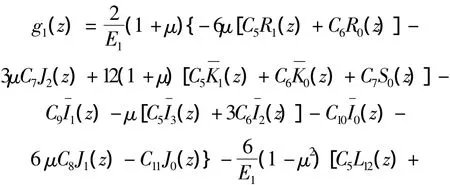
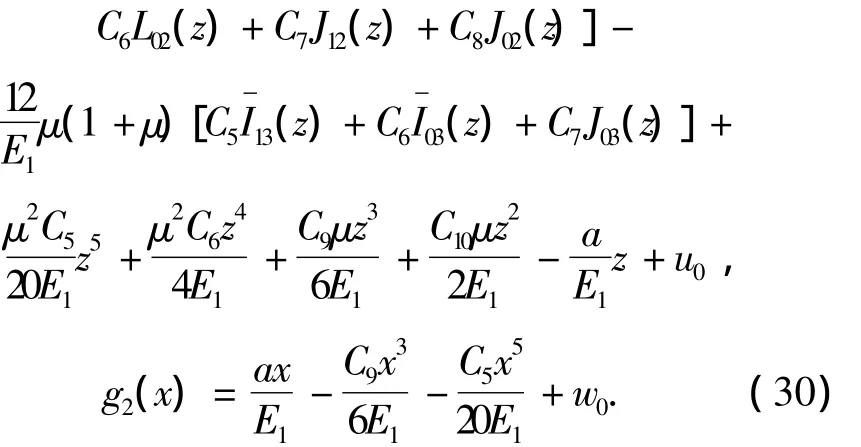
式中:u0、w0为待定的常数，积分函数如下:

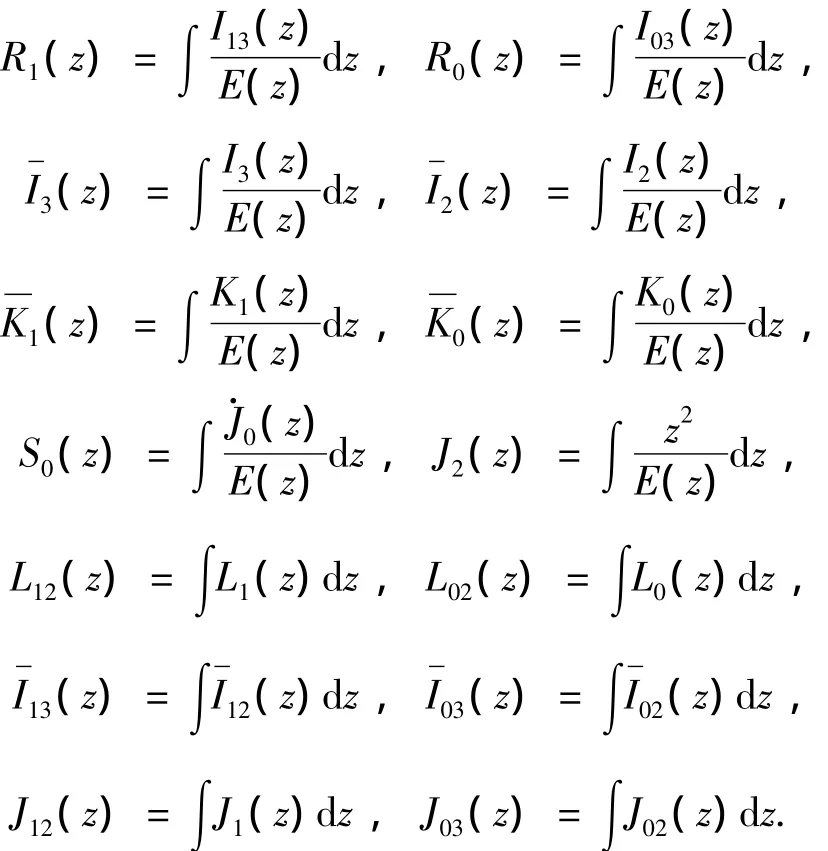
考虑位移的边界条件式(11)，则可以得出

解之得，可以求出各常数的数值:

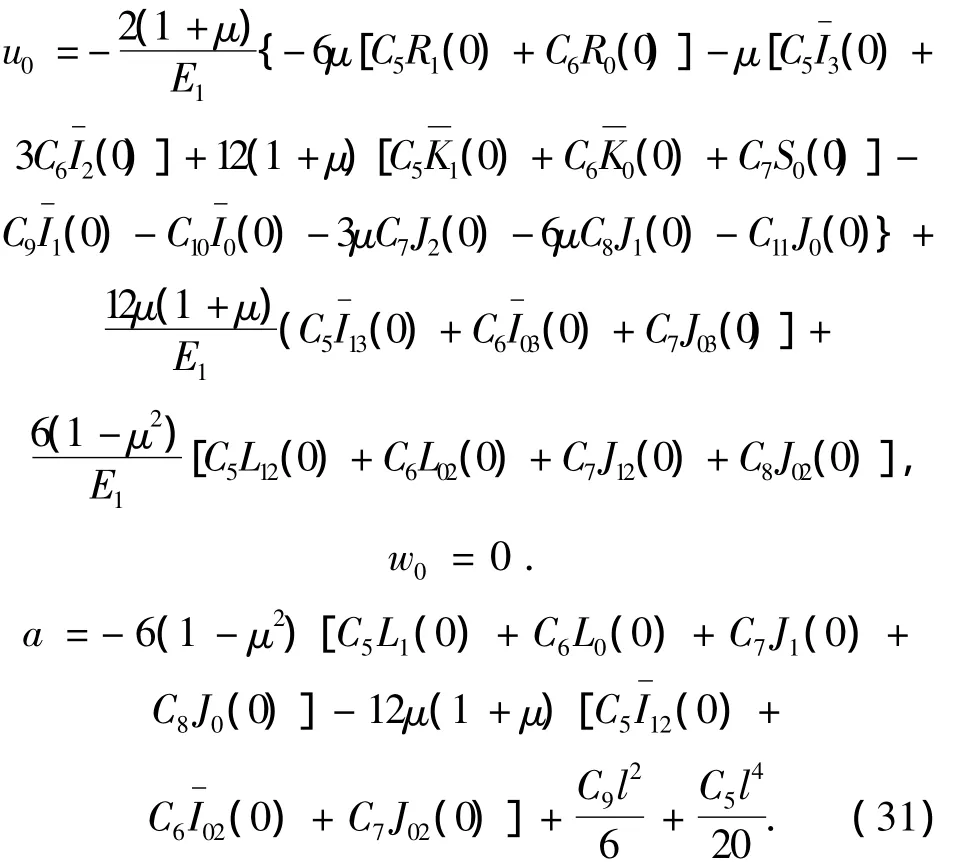
将式(30)、(31)代入式(28)，即可得出轴向位移和挠度在整个梁上的分布.

3 功能梯度简支梁在线性载荷作用下的弯曲分析

算例1 计算弹性模量在厚度方向上呈线性分布的功能梯度简支梁在线性载荷作用下的变形，此时对应的弹性模量分布函数为

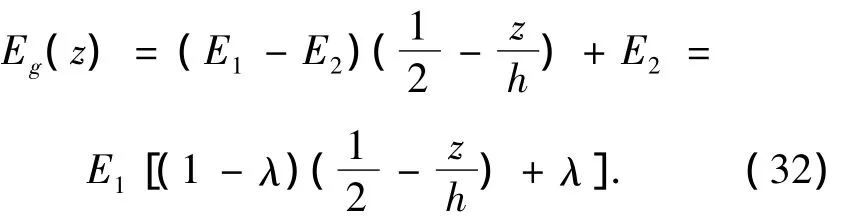
式中:E1、E2分别为上下表层材料的弹性模量，λ=E2/E1为下表层与上表层材料弹性模量的比值，当λ为1时表示均质各向同性梁.采用如下材料参数:E1=210 GPa，μ =0.3，p=1 kPa，l=10 m，h=1 m，b=1 m，λ =1/1 000.

为验证本文方法的正确性，采用有限元仿真软件进行计算，将简支梁在厚度方向上利用20层等厚度的均质材料进行离散，模拟功能梯度梁弹性模量在厚度方向上的变化.在两端采用MPC约束方式施加简支边界条件，并采用三维实体线性缩减单元C3D8R建立有限元计算模型.将本文方法求得的z=-h/2处的挠度的解析解与有限元仿真结果进行对比，如图2所示.

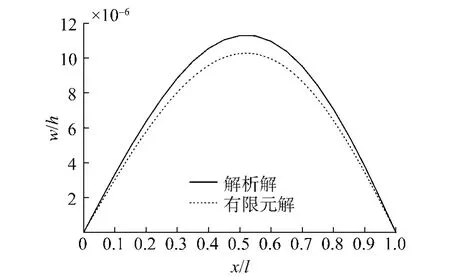
图2 解析解与有限元解的挠度对比Fig.2 The comparisons of deflection curves between analytical and FEM solutions

从图2中可以看出，由本方法求出的挠曲线与有限元仿真结果十分相近，解析解得出的最大挠度为11.29，而有限元仿真得出的最大挠度为10.27，两者相差9%，符合工程应用要求，这也证明了本文计算方法的正确性.两者之所以存在一定的误差，主要是由于有限元计算中采用了有限层均质材料来模拟功能梯度材料，当采用的层数越多时其结果将和解析解更加相近.

算例2 计算材料属性在厚度方向上连续变化的功能梯度简支梁的应力应变和位移的分布.其材料属性(弹性模量)的变化遵循最常用的幂律分布［10-11］，即

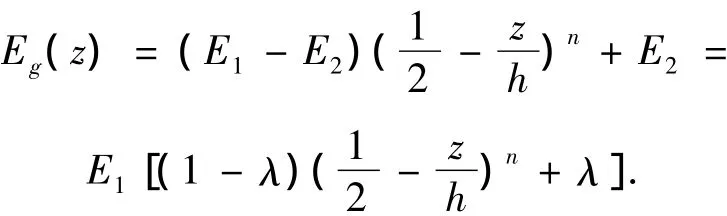
式中:n为组分材料体积分数指数，其他参量的意义与式(32)相同.在计算中，n 分别取1、2，λ 分别取1、1/100、1/10 000，以研究λ及n对挠度与应力分布影响.

通过计算，得出了在各种材料分布状况下功能梯度梁中的应力和位移的分布.分别给出了x=l/2处横截面上无量纲 σx、σz与 τxz的分布曲线以及z=-h/2处的无量纲挠度在整个梁上的分布曲线，如图3～6所示.

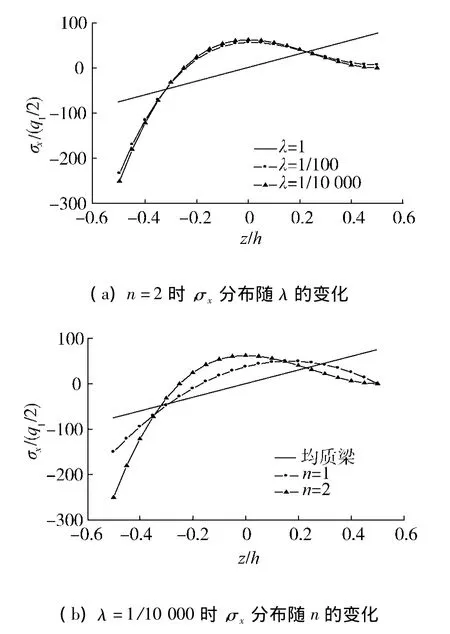
图3 x=l/2处，σx在梁厚度上的分布Fig.3 The variation ofσx across thickness at x=l/2

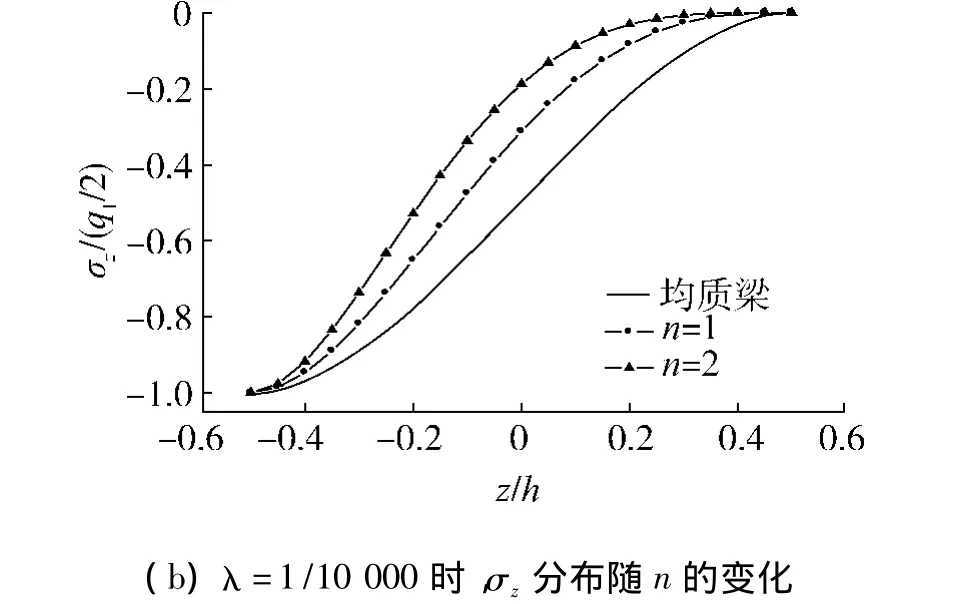
图4 x=l/2处，σz在厚度上的分布Fig.4 The variation of σz across thickness at x=l/2

图5 x=l/2处，τxz在厚度上的分布Fig.5 The variation of τxz across thickness at x=l/2

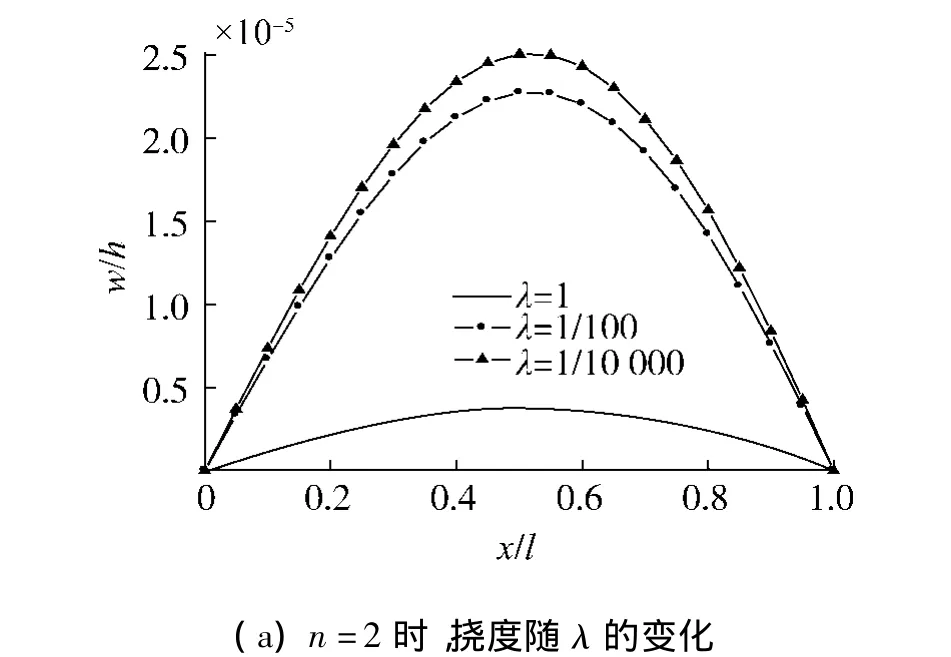
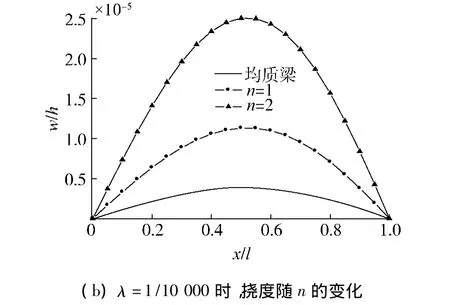
图6 z=－h/2处的挠度曲线Fig.6 The curves of deflections at z= －h/2

从图3、4可以看出，在功能梯度梁中，当材料属性遵循幂律分布时，厚度方向上σx、σz均呈现非线性分布;在上表层承受线性分布载荷，且λ＜1时，梁横截面内的最大x向压应力出现在上表层，而在几何中面与上表层之间的位置处，x向拉应力最大，且其随着n的增大，不断向上表层靠近.从图5中可以看出，在功能梯度梁中，τxz的分布不再关于几何中面对称，其最大值偏向于弹性模量较大的一侧.从图6中可以看出，在线性载荷作用下，功能梯度梁的最大挠度值出现在偏向较大载荷的一侧，而n与λ对挠度的影响是相反的，梁的最大挠度值随着λ值的增大而减小，随着n值的增大而增大.

4 结束语

利用应力函数法，研究了线性分布载荷作用下功能梯度简支梁弯曲问题的解析解，并得到了针对以上问题的应力函数的表达式，给出了各向应力应变与位移的显式解析计算式;并分析了材料属性在厚度方向上遵循幂律分布的功能梯度简支梁中，体积分数指数n和上下表层材料弹性模量比λ对各向应力与位移的影响规律.可以看出应力函数法不但可以精确地描述功能梯度简支梁的应力分布和变形问题，还可以做进一步的推广和应用.

［1］KOIZUMI M.FGM activities in Japan［J］.Composites，Part B:Engineering，1997，28B:Engineering:1-4.

［2］CHISH，CHUNG Y L.Mechanical behavior of functionally graded material plates under transverse load-Part I:analysis［J］.International Journal of Solids and Structures，2006，43:3657-3674.

［3］GILHOOLEY D F，BATRA R C，XIAO JR，et al.Analysis of thick functionally graded plates by using higher-order shear and normal deformable plate theory and MLPGmethod with radial basis functions［J］. Composite Structures，2007，80:539-552.

［4］仲政，于涛.功能梯度悬臂梁弯曲问题的解析解［J］.同济大学学报:自然科学版，2006，34(4):443-447.ZHONG Zheng，YU Tao.Analytical bending solution of functionally graded cantilever-beam［J］.Journal of Tongji University:Natural Science，2006，34(4):443-447.

［5］于涛，仲政.均布荷载作用下功能梯度悬臂梁弯曲问题的解析解［J］.固体力学学报，2006，27(1):15-20.YU Tao，ZHONG Zheng.A general solution ofa clamped functionally graded cantilever-beam under uniform loading［J］.Actamechanica Solida Sinica，2006，27(1):15-20.

［6］SANKAR B V.An elasticity solution for functionally graded beams［J］.Composites Science and Technology，2001，61:689-696.

［7］黄德进，丁皓江，陈伟球.任意载荷作用下各向异性功能梯度梁的解析解和半解析解［J］.中国科学G辑:物理学力学 天文学，2009，39(6):830-842.HUANG Dejin，DING Haojiang，CHEN Weiqiu.Analytical and semi-analytical solutions of anisotropic functionally graded beams subjected to arbitrary load［J］.Science in China，2009，39(6):830-842.

［8］徐芝纶.弹性理论［M］.北京:高等教育出版社，2006:41-45.

［9］黄德进，丁皓江，陈伟球.线性分布载荷作用下功能梯度各向异性悬臂梁的解析解［J］.应用数学和力学，2007，28(7):763-768.HUANG Dejin，DING Haojiang，CHENWeiqiu.Analytical solution for functionally graded anisotropic cantilever beam subjected to linearly distributed load［J］.Applied Mathematics and Mechanics，2007，28(7):763-768.

［10］GHARIB A，SALEHIM，FAZELI S.Deflection control of functionally graded material beams with bonded piezoelectric sensors and actuators［J］.Materials Science and Engineering A，2008，498:110-114.

［11］SAHRAEES.Bending analysis of functionally graded sectorial plates using Levinson plate theory［J］.Composite Structures，2009，88:548-557.