高维情况下双差整周模糊度LAMBDA法解算分析

程建华，王晶，晏亮，时俊宇

(1.哈尔滨工程大学自动化学院，黑龙江哈尔滨150001;2.北京航天时代激光导航技术有限责任公司设计部，北京100143)

最小二乘降相关平差法(least-squares ambiguity decorrelation adjustment，LAMBDA)去相关处理即将双差模糊度的估计值通过整数Z变换映射到相关度相对较小的空间内，使模糊度协方差矩阵趋近于对角阵，最终完成模糊度的快速搜索.由于双差模糊度具有高度相关性，去相关处理效果的好坏直接影响之后的搜索效率高低.研究发现当在高维网络式或多基线、多频率解算的工作模式下，LAMBDA算法经常失效[1]，这极大地限制了这一快速解算方法的应用，因此分析高维情况下LAMBDA算法解算效果对于扩展其应用范围具有重要的研究价值.

国内外学者对于LAMBDA算法提出了不同的改进意见[2-4]，但都针对去相关速度进行改进，而1998年Li and Gao提出的高维改进算法也只是在7～13维内有效[1].XU Peiliang 等[1]首次分析了不同去相关算法在不同工作模式下的解算效果，发现在高维网络式的工作状态去相关算法经常失效，但没有从理论角度对这种状况进行分析.X W Chang等[4]讨论了LAMBDA法去相关的不完全性，但未对不同模式下算法的效果进行具体分析，仍然只是改进了去相关的解算效率.Kuylen，Monikes以及Wang等在多基线的姿态测量中，利用基线长度的限制解决该模式下的模糊度解算问题[5-6];Teunissen等[7]提出的MC LAMBDA方法利用旋转矩阵的正交性来限制模糊度估计参数，使得LAMBDA方法在多基线姿态测量中得到应用.但都没有对解决高维解算问题给出一般性的结论.高维去相关解算失效会使最终模糊解算的正确率降低，从而使得精确定位失去意义.

本文对Teunissen等[8]提出的LAMBDA方法中采用的去相关处理方式进行深入分析，通过研究算法的实现原理，对高维情况下去相关处理效果进行讨论，并给出相关结论.

1 矩阵去相关评价指标

对矩阵去相关处理效果分析主要有2个参数:矩阵条件数和相关系数.

1.1 矩阵条件数

矩阵条件数是判断矩阵病态与否的一种度量，条件数越大矩阵越病态.矩阵的条件数与其奇异值有关，奇异度可以通过列或行向量的相关性刻画，值越大相关性越强.矩阵的条件数c定义为矩阵的最大与最小奇异值的比值，对于正定对称矩阵来说，奇异值与矩阵特征值相等，即

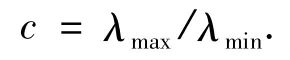
1.2 相关系数

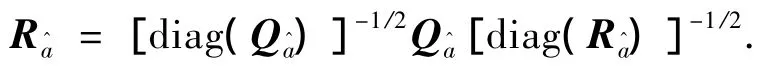
对于n维情况，相关系数矩阵中包含n(n-1)/2个相互独立的相关系数，当n很大时若想对每个相关系数都进行评价是很不现实的，需要用某种相关系数的标量函数来衡量的对角化程度.在实际应用中通常是直接计算det()的平方根作为衡量模糊度去相关程度指标，于是有相关系数表达式:

2 LAMBDA法去相关效果评价

2.1 LAMBDA去相关原理

基于LAMBDA法的双差模糊度求解，是通过一个整数变换来对模糊度进行解相关处理，然后利用序贯条件最小二乘的方法求解模糊度整数值.

序贯条件最小二乘是利用模糊度的条件方差求取模糊度的条件估值并建立搜索空间来寻求模糊度的最优估值.其中条件方差的确定利用对协方差矩阵的Cholesky分解得到

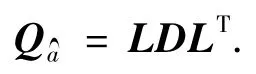
式中:L为单位下三角阵;D为对角矩阵，即条件方差矩阵.

然而，对于高度相关的双差模糊度来说，仅通过这样的计算往往无法取得成功，必须通过去相关处理使协方差矩阵尽量对角化以提高搜索的效率以及成功率，这也是整数变换的目的.此过程的目标是:1)尽量使得矩阵对角化;2)对角阵D的元素按降序排列.具体的去相关过程如下.

2.1.1 整数高斯变换

为了降低相关性，首先从矩阵L的对角化变换入手，利用整数高斯消去法使矩阵非对角位置元素大小不超过0.5.循环进行二维的整数高斯变换实现对矩阵L所有非对角位置元素的更新.变换因子中，令 α =-［li+1，i］.

通过上述过程即可实现矩阵L的对角化，但在实现过程中并没有对矩阵D进行相应的更新操作，因此需要下面的步骤实现.

2.1.2 排序

矩阵D的更新排序是利用初等变换矩阵P实现的.

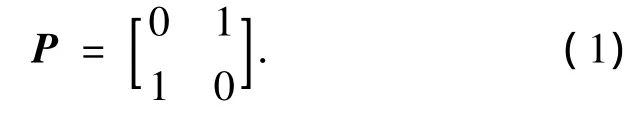
式(1)变换作用到矩阵L、D的第i、i+1行和列上引起的二维变换结果为

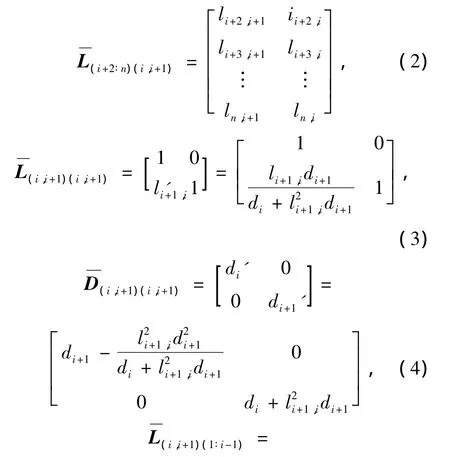
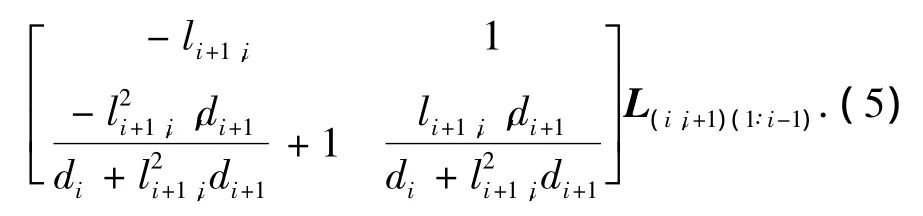
在式(2)～(5)的更新过程中以di+1' ≥di+1为判定标准，当满足此条件时，更新完成.

按照矩阵列从右至左的顺序经过以上步骤，遍历矩阵所有元素，即完成了对于协方差矩阵的去相关处理，最终得到转换矩阵Z.

2.2 去相关效果仿真

以矩阵条件数和相关系数作为参考，采用随机模拟[1，9]的方法分别对低维和高维情况下去相关效果进行仿真，结果如图1和2所示.

1)相关性小、维数低，仿真结果见图1.使随机产生的200个正定对称矩阵的条件数对数值在[0，4.5]范围内随机取值，维数相对较低，范围设为[3，10].

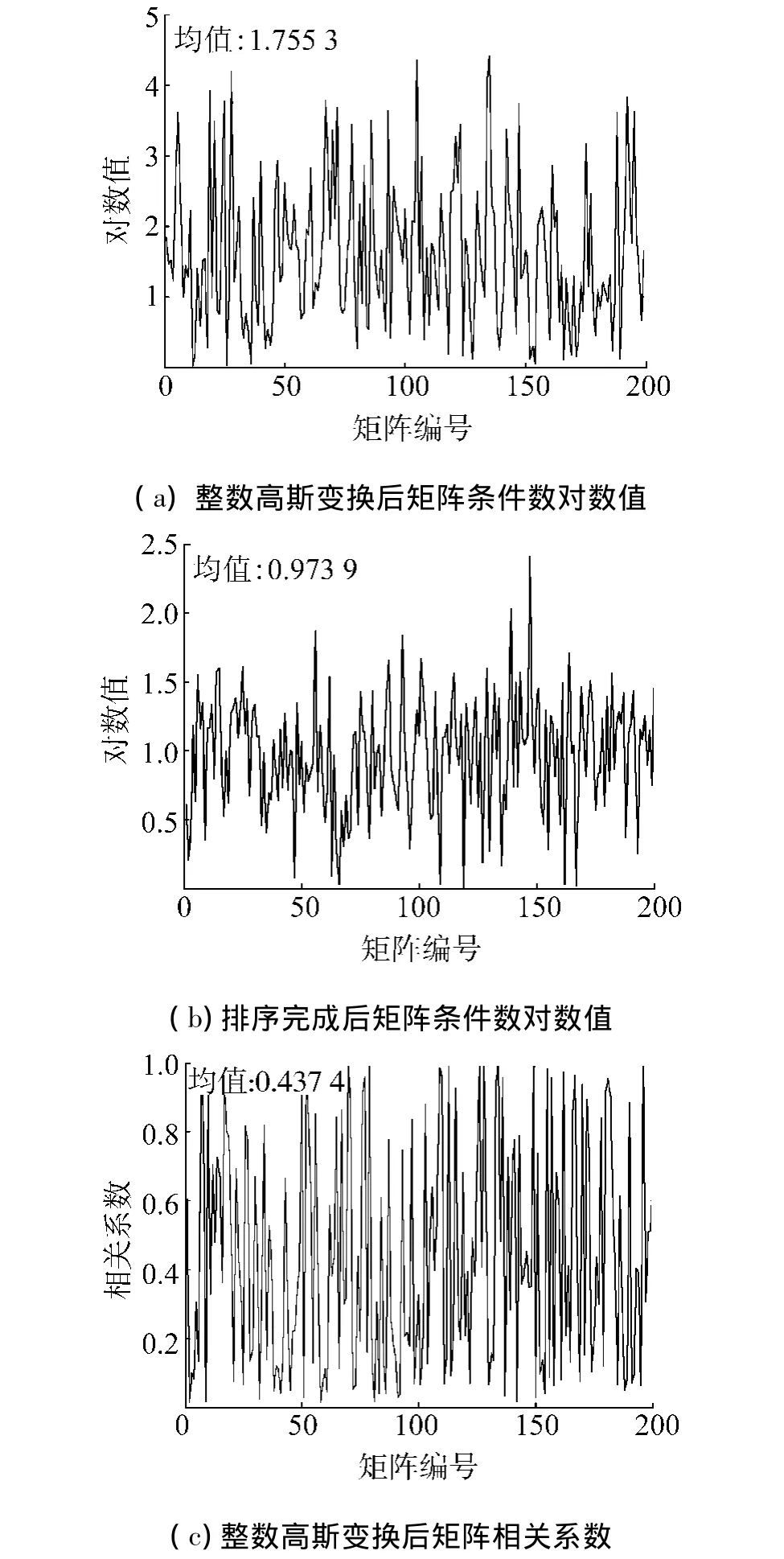
图1 低维矩阵去相关过程中指标对比曲线Fig.1 The comparison of the index curves during decorrelation process in low dimensional matrix

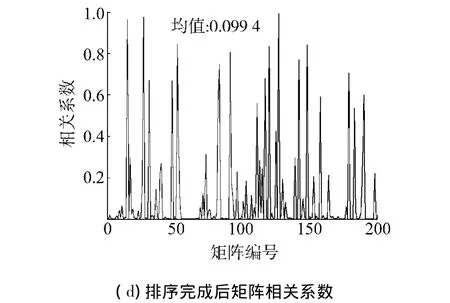
图2 高维矩阵去相关过程中指标对比曲线Fig.2 The comparison of the index curves during decorrelation process in high dimensional matrix

2)相关性大、维数高.使随机模拟的协方差矩阵的条件数相对较高，取条件数对数值范围[3，4.5]，并且随机维数也在一个较高的范围内，取其范围[11，50].

通过对仿真数据的分析，发现在低维情况下，从只进行整数高斯变换到同步执行排序过程的去相关程度要优于高维情况.而且，从最终结果的相关指标来看，高维情况的相关性仍然保持在一个较高的水平上，且会出现相关性变差的情况.这是由于高维条件下初始协方差矩阵的相关性就非常高，这样的去相关程度无法满足最终模糊度搜索的正确性和高效性，有时会导致搜索无效.因此，在高维情况下，采用LAMBDA法解算整周模糊度的效果并不理想.那么分析高维失效的原因就成为了解决这一问题的关键所在.

3 LAMBDA法去相关高维解算分析

根据仿真情况，分析高维解算效果不理想的原因，首先要分析LAMBDA算法的去相关处理过程，结合矩阵的相关性指标给出结论.

3.1 LAMBDA去相关解算分析

3.1.1 整数高斯变换分析

在整数高斯变换完成后，实现了矩阵L的对角化.对LDLT作奇异值分解，由于它近似对角阵，那么矩阵D的对角元素可以认为是矩阵的奇异值，分析结果矩阵LDLT的条件数，矩阵D中最大元素除以最小元素:c=d(i)max/d(i)min.

显然对角矩阵的元素之间是相互独立的，条件数会较整数变换前明显变小.

然后，分析矩阵变换前后相关系数的变化情况，在对协方差矩阵进行Cholesky分解中，矩阵D元素与分解前协方差矩阵的关系:

从式(6)可以发现，D中的元素是矩阵Q)a对角元素减去对应L阵第i行前i-1个元素的平方和.显然，D中的元素在原协方差矩阵对角元素的基础上减小了.LDLT矩阵的相关系数:

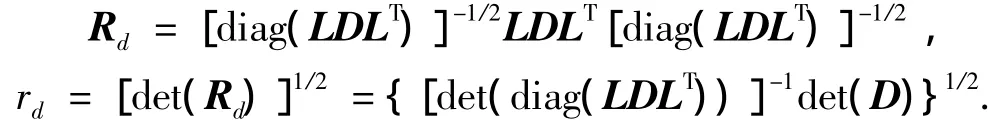
协方差矩阵Q)a的相关系数:

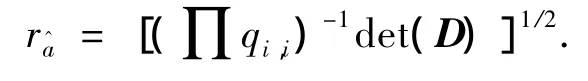
显然变换后矩阵的相关系数减小.

从模糊度搜索的角度分析，由于整数高斯变换过程中矩阵D没有变化，即条件方差没有改变，分析序贯条件最小二乘模糊度的求取式(7)以及利用条件方差搜索最优模糊度解的式(8):

可以发现，对于矩阵L的更新，改善了对序贯条件最小二乘模糊度的求取过程，降低了前后模糊度的相关性，有利于序贯条件最小二乘模糊度的求解.但在模糊度的搜索过程中条件方差是决定搜索空间大小和搜索效率的关键因素，条件方差按照降序排列是保证搜索效率的必要条件.

3.1.2 排序过程分析

从LAMBDA法去相关过程可以发现，矩阵D元素完成排序交换的同时，矩阵L的非对角位置元素会随之更新，元素大小保持在小于0.5的范围内.而对更新后的矩阵D元素作差得

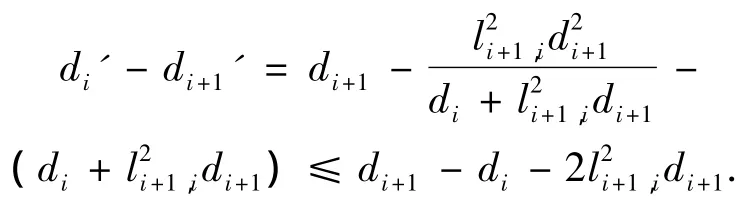
显然变换后相邻元素之间的差距变小.总体上来说，排序过程实现的是上一步骤中LDLT矩阵交换行列次序的功能，在变换过程中矩阵的相关性得到进一步的改善.

但仿真结果显示，在高维情况下排序过程的去相关程度并没有低维情况的效果显著，因此有必要对条件方差的更新过程进行更进一步的分析.

3.2 条件方差连续性分析

条件方差的大小体现了当前模糊度与前面模糊度的相关程度，根据条件模糊度求取公式:

由D中相邻元素间的距离更新关系式:

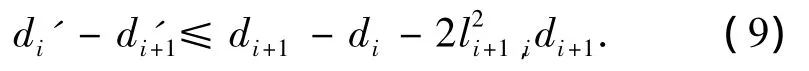
可知，距离值在变小.而从矩阵D的更新过程来看，第一个元素的值保持不变，为了减小相邻模糊度之间的距离，后面的条件方差值都有所提升，从而实现了降低相邻模糊度之间相关性的目的.同时从矩阵条件数角度来分析也可知，矩阵的最小特征值变大，矩阵的条件数减小.

下面通过仿真［10］观察矩阵D元素更新前后的变化情况，分别对维数为8和29的协方差矩阵进行仿真，如图3.

从结果可知，去相关处理后条件方差的连续性得到改善，这样降低了双差模糊度的相关性.而在高维情况时去相关处理后的曲线的平滑程度并不理想，这就使得LAMBDA方法在进行高维解算时没有达到理想的效果.而这样的结果与矩阵D的更新分解过程直接相关，即排序过程在高维情况下存在不完善的问题.

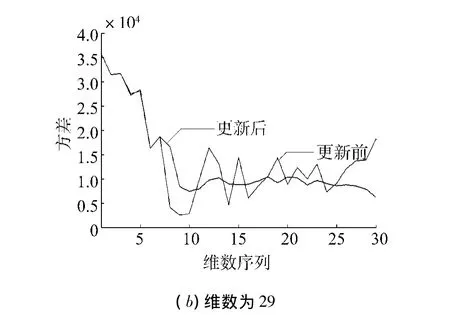
图3 去相关前后模糊度条件方差分布Fig.3 The distribution of conditional variance before and after decorrelation

3.3 高维解算时排序更新分析

LAMBDA算法排序最终目的是使更新后矩阵D中所有元素都按照降序排列，判断矩阵D相应位置元素是否更新完成的依据:

这个条件暗指di＜di+1，如果条件满足则需要进行更新.这是因为如果更新后的di+1' 比更新前的值小，说明相应位置的模糊度与其后模糊度的相关性并未得到改善，必须进行更新，将条件方差提高，这也是条件方差降序排列的依据.与此同时，矩阵D位置i的元素以及矩阵L相应位置元素也要进行更新:

当更新完成后对于新的矩阵D将会满足:

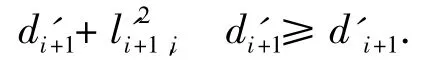
即

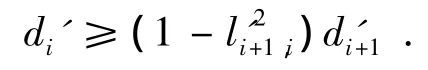
由此可知，这并不能保证更新完成后矩阵元素满足di'≥di+1'，只能使相邻2个值之间的差距减小，从而保证降序排列.如果要以di'≥di+1'为判定依据进行矩阵D更新，由上面的关系式中可以看出，这样的条件很难满足，将会花费大量的时间，使得快速解算失去意义.

同时，更新过程中li+1，i' 会出现增大的趋势，而使得其结果超出0.5的范围，即相邻2个模糊度的协方差会变大，最终使得协方差矩阵对角化效果变差.

由此可以明确，更新过程并不是严格按照条件方差降序排列的标准进行的，只是修正了连续性，这种处理是不彻底的，而且会对上一步的整数高斯变换结果产生一定的影响.对于维数较低即维数范围为[3，10]的情况，这种影响体现的不明显.当处理高维数据时，由于较高的相关性，排序处理次数增多，而使得对于矩阵L的更新增多，不但相关性变差，受更新条件的限制，降序排列也不完全，严重影响了相关性处理的效果.

因此，当进行高维解算时，将会存在去相关不彻底的情况，而使得最终的模糊度搜索效率受到影响，甚至无法得到正确解.

4 仿真分析验证

为了验证以上分析结果的正确性，下面分别对低维和高维去相关解算结果进行仿真分析.对于2种工作模式下得到的更新矩阵D，即新的条件方差进行重新的降序排列，将初等变换矩阵作用在变换后的协方差矩阵上.对随机模拟生成的协方差矩阵条件数进行前后结果的比较如图4所示.

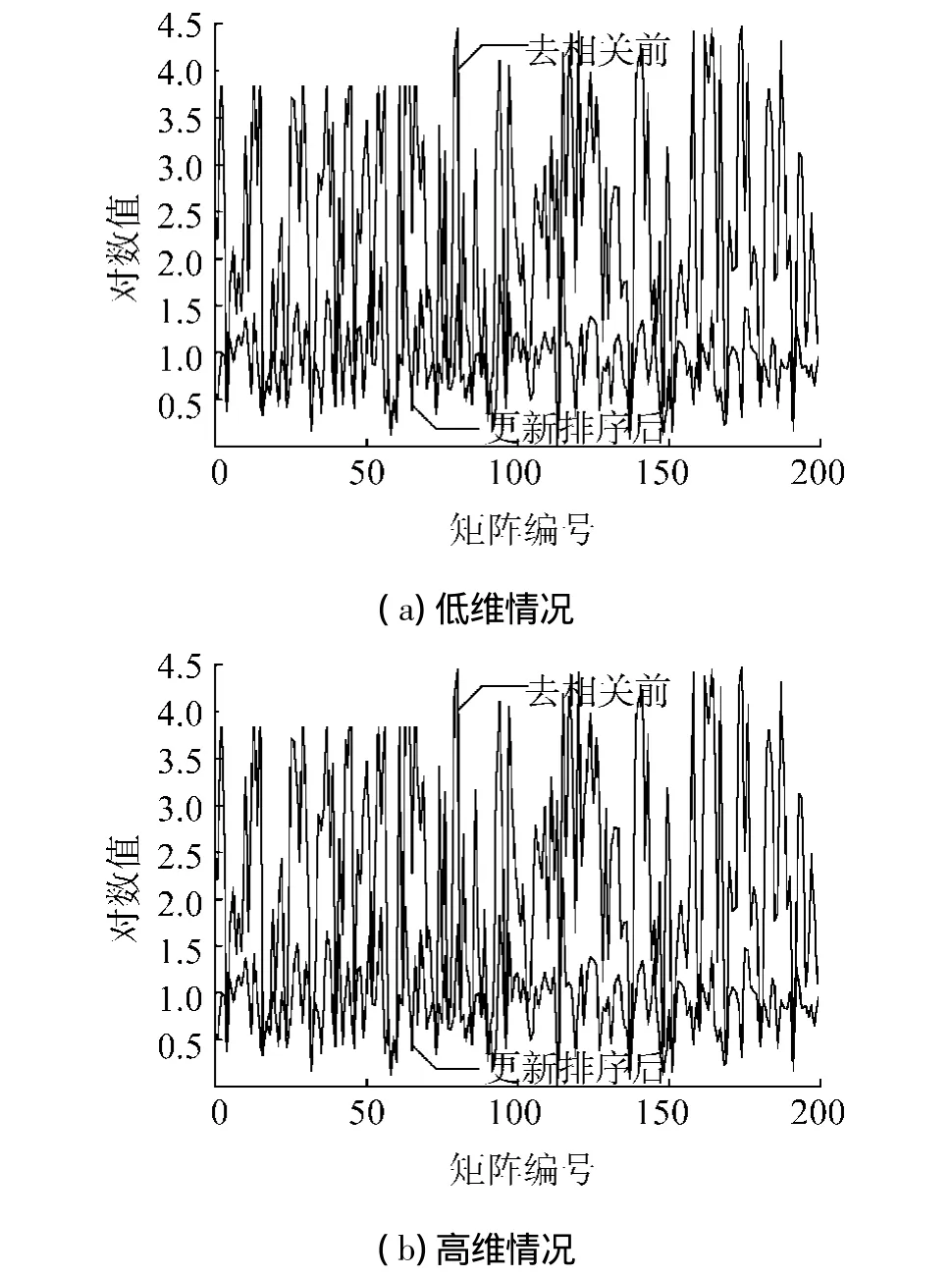
图4 条件方差重列后矩阵条件数Fig.4 The condition number of matrix after reorder of conditional variance

从图4中可以看出，对比之前LAMBDA法分别在两种模式下的仿真结果看，低维情况下的结果并没有太大变化;而对于高维情况，矩阵的条件数在经过重新排列后明显降低了.这说明，LAMBDA算法的低维去相关处理是比较彻底的，而高维情况会明显失效.

5 结束语

对LAMBDA法求解双差整周模糊度在高维情况下失效的问题进行深入分析，从去相关解算过程的分析中发现，在对模糊度条件方差进行排序处理时没有进行完全的降序排列，当解算维数提高时，这种处理的不完全性就会明显体现出来，而致使模糊度相关性处理得不到有效改善.而当对条件方差进行后续降序排列处理后，得到的协方差矩阵的相关性指标得到明显改善，由此证明，本文对于LAMBDA法高维解算失效原因分析的正确性.

[1]XU Peiliang.Random simulation and GPS decorrelation[J].Journal of Geodesy，2001，75(7):408-423.

[2]HAN Shaowei，RIZOS C.A new method for constraining multisatellite ambiguity combinations for improved ambiguity resolution[J].Journal of Geodesy，1995，70(9):1145-1153.

[3]LIU L T，HSU H T，ZHU Y Z，et al.A new approach to GPS ambiguity decorrelation[J].Journal of Geodesy，1999，73(9):478-490.

[4]CHANG X W，YANG X，ZHOU T.A modified LAMBDA method for integer least-squares estimation[J].Journal of Geodesy，2005，79(9):552-565.

[5]GIORGI G，TEUNISSEN P J G，VERHAGEN S.Testing a new multivariate GNSS carrier phase attitude determination method for remote sensing platforms[J].Advances in Space Research，2010，46(2):118-129.

[6]TEUNISSEN P J G，GIORGI G，BUIST P J.Testing of a new single-frequency GNSS carrier phase attitude determination method:land，ship and aircraft experiments[J].GPS Solution，2011，15(1):15-28.

[7]TEUNISSEN P J G.A general multivariate formulation of the multi-antenna GNSS attitude determination problem[J].Artificial Satellites，2007，42(2):97-112.

[8]TEUNISSEN P J G.The least-squares ambiguity decorrelation adjustment:a method for fast GPS integer ambiguity estimation[J].Journal of Geodesy，1995，70:65-82.

[9]XU Peiliang.Spectral theory of constrained second-rank symmetric random tensors[J].Journal of Geophysics，1999，138:1-24.

[10]TEUNISSEN P J G，JONGE P，TIBERIUS C.On the spectrum of the GPS DD-Ambiguities[C]//Proceedings ION GPS-94.Salt Lake City，USA，1994:115-124.