新型混合粒子群算法在核动力设备优化设计中的应用

阎昌琪，刘成洋，王建军

(哈尔滨工程大学核科学与技术学院，黑龙江哈尔滨150001)

Kennedy与Eberhart通过对鸟群觅食过程的分析及模拟，于1955年最先提出了原始的PSO(particle swarm optimization)算法[1]，其中关于如何加快算法的收敛速度、收敛精度和避免早熟收敛问题，一直是研究者们关注的重点，也是所有随机搜索算法共同面临的主要难题.目前多数粒子群算法主要针对无约束优化问题研究，而实际工程中的优化问题往往具有约束条件.惩罚函数法是进化算法处理约束问题的常用方法[2]，但其主要缺点是惩罚参数的选取比较困难，而算法在很大程度上依赖于参数的选取，所以参数与具体优化问题有关.本文在对各种改进PSO算法研究的基础上，提出了一种新型混合粒子群算法(new hybrid particle swarm optimization，NHPSO).在约束处理方面，采用应用比较广泛的可行性原则[3-6]进行约束处理;参照文献[7]，运用复合形算法产生初始可行群体;引入遗传算法中的交叉和变异策略[8-9];利用改进复合形算法[10]在优解附近进行局部搜索.

1 新型混合粒子群算法

1.1 非线性约束问题

具有D个决策变量，m个约束条件的非线性约束问题可以描述为

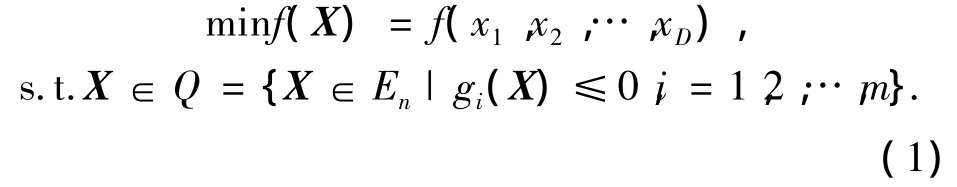
1.2 标准粒子群算法

在标准粒子群算法中，单个粒子如 Xi={xi，1，通过跟踪 2 个极值来更新自己，其中表示第i个个体极值的第d维变量表示当代全局极值的第d维变量.粒子变量的速度和位置的更新方式为

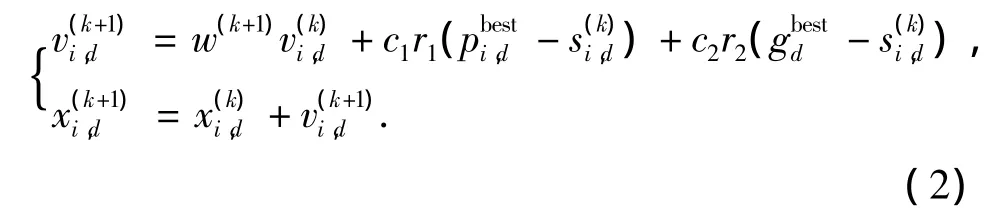
1.3 可行性判断规则

定义1 随机产生一个个体，若该个体满足约束条件，则该个体称为可行个体，若该个体不满足约束条件，则称该个体为不可行个体.

适应度表示个体X对环境的适应程度，将适应度分为两类:1)针对被优化的目标函数的目标型适应度，2)针对约束函数的约束型适应度.其中目标型适应度和约束型适应度分别表示为

式中:si为不同约束条件的权重

对于求最小值的约束优化问题，对群体中所有粒子按照适应度进行排序，基本规则是:

规则1 比较粒子的约束型适应度，如果2个粒子约束适应度都为0，即2个粒子都在可行域内，那么目标型适应度小的粒子排序靠前.

规则2 如果一个粒子在可行域内，而另一个在可行域外，那么可行域内的粒子排序靠前.

规则3 如果2个粒子都在可行域外，那么违反约束程度较小的粒子排序靠前.

与通常的惩罚函数方法相比，这种方法的优点是可行点的目标型适应度总是优于非可行点的目标型适应度，且无需变换优化目标的适应度到大于零，使用较为简单.

1.4 产生初始可行群体

通过标准粒子群算法迭代式(2)可以发现，算法的收敛速度主要取决于粒子历史最优位置和群体最优位置，而如果最优位置不满足约束条件则算法的收敛速度会减慢，甚至可能陷入局部最优.有些情况下，由于优化问题约束函数多，因此初始可行群体的随机产生很费时间，而引入复合形算法的过程可以加快初始可行群体的产生.其基本过程如下:

1.5 交叉变异策略

在粒子群算法中引入遗传算法的交叉和变异策略，可使群体保持多样性，利于算法跳出局部最优.

1.5.1 交叉算子

设计了一种新的交叉算子，其基本思想是在交叉之后，一点落于进行交叉的两父代之间，一点落于靠近较好的父代的一侧，使解向好的方向发展，并且都是可行解.

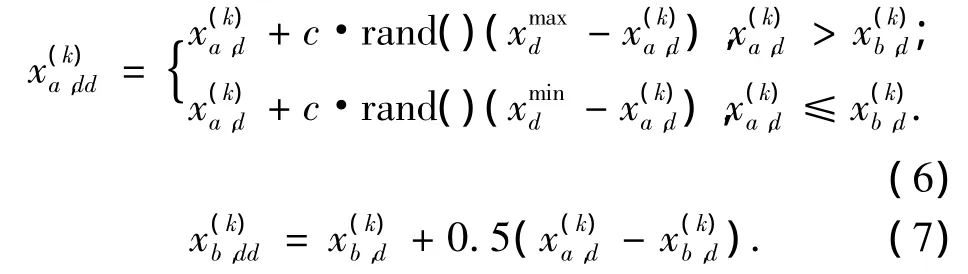
1.5.2 变异算子

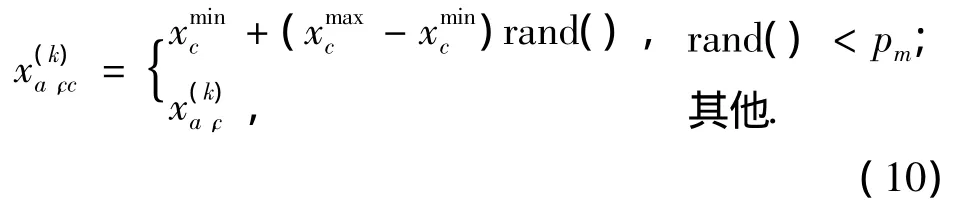
1.6 NHPSO流程和算法测试

由于篇幅所限，文献[10]的改进复合形算法的具体步骤在此不列出，新型混合粒子群算法具体流程图见图1所示.

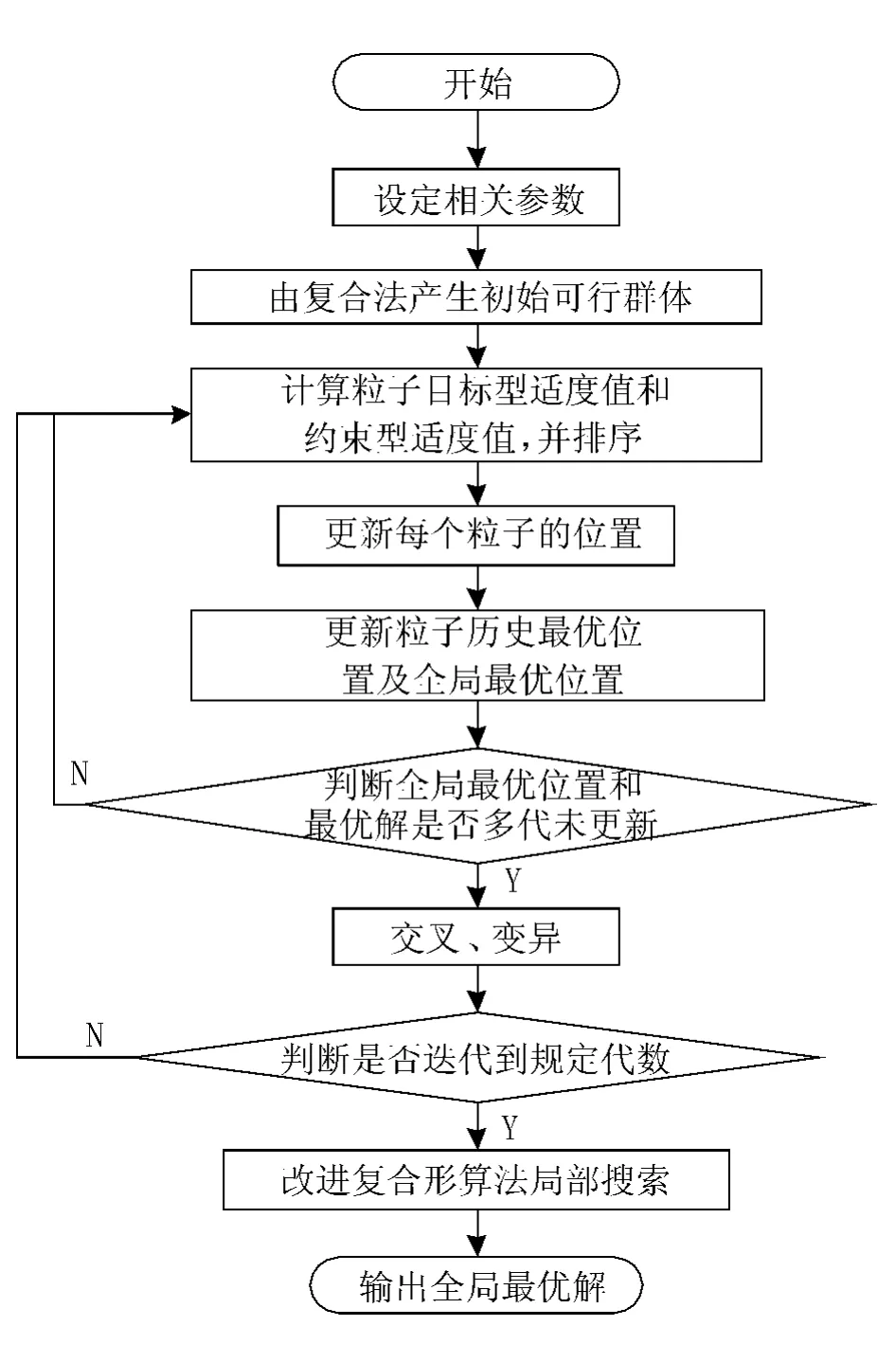
图1 NHPSO流程Fig.1 The flow chart of NHPSO

在测试函数的选取上，使用目前关于约束优化较完整、使用较多的基准测试函数，即在文献[11]中总结的测试函数集g01～g13，这13个测试函数各有特点，各有难度，本文以g06和g09这2个函数对算法的有效性进行测试.

函数g06:

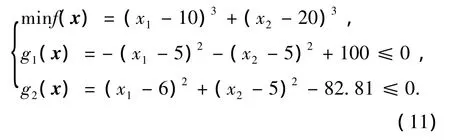
式中:13≤x1≤100，0≤x2≤100.最优解位于x*=(14.095，0.842 96)，最 优 值 为 f(x*)=-6 961.813 88.该问题的可行域占搜索空间的比值为0.57‰，因此算法需要有较好的搜索探测能力.函数g09:

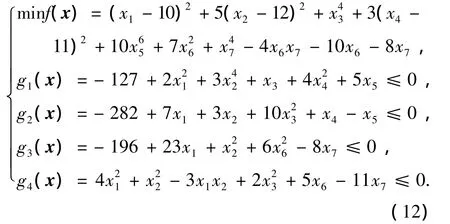
式中:-10≤xi≤10(i=1，2，…，7).最优解位于x*=(2.330 499，1.951 372，-0.477 541 4，4.365 726，-0.624 487 0，1.038 131，1.594 227)，最优值为f(x*)=680.630 057 3.该问题的可行域占搜索空间的比值为0.519 9%.

实验参数的选择:c1=c2=2.0，w0=0.9，w1=0.5.取粒子数为50，运行100代，每个测试用例均在相同条件下独立运行20次.在表1中，本文NHPSO算法结果为20次运行平均值，FSM-PSO和PFMPSO算法结果取自文献[12]，Sel-PSO算法结果取自文献[13]，M-PSO取自文献[14].

从表1可以看出，在优化g06时，NHPSO算法与M-PSO算法优化程度相当，明显优于其他算法;在优化g09时，NHPSO的算法结果最接近最优解.可见，NHPSO具有很好的精度与稳定性.

失眠是抑郁症的典型症状，同时也是导致抑郁的重要原因。许多朋友就是由于严重失眠得不到缓解而被考虑为抑郁症的。

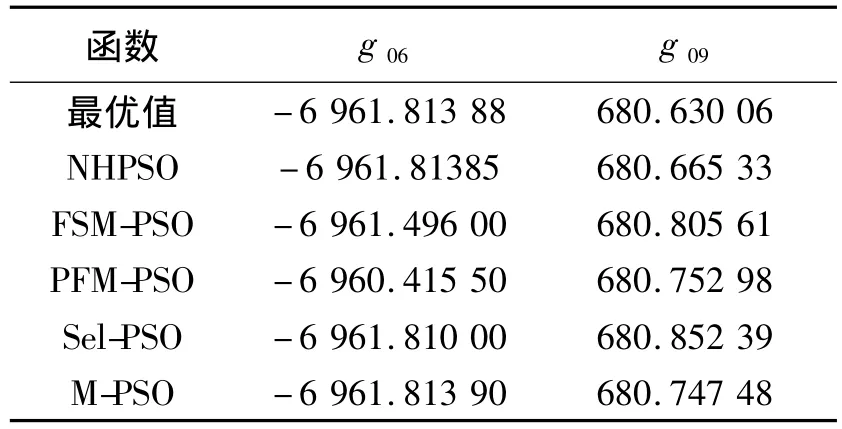
表1 测试函数最优值和算法结果Table 1 Test functions optimal value and algorithm results

图2为g06和g09这2个函数每代的最优目标函数值与理论最优解的比值.从图中可以看出，在35代之前，目标函数值向理论最优解快速靠近，在35代之后基本达到理论最优解，可见NHPSO有极高的快速收敛性.

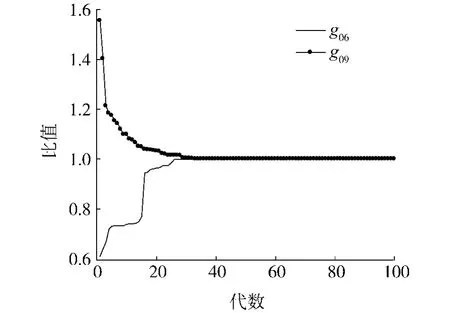
图2 目标函数值与理论最优解的比值Fig.2 The ratio of objective function values and the optimal theory solution

2 核动力设备优化设计

基于上述开发的NHPSO算法，下面对一回路中的蒸汽发生器和二回路中的冷凝器进行优化设计，其中蒸汽发生器模型和冷凝器模型分别见文献[15-16].

2.1 蒸汽发生器重量优化设计

对于蒸汽发生器重量优化问题，选定一回路运行压力P、传热管外径dco和传热管节径比sc/dco这3个参数为优化变量.

考虑热力性能、生产和施工等实际因素，蒸汽发生器重量优化设计的约束条件主要有:循环倍率、循环速度、蒸汽发生器高度、管束直径和传热管总根数，均在一定范围内.

蒸汽发生器优化设计结果如表2所示，其中各参量都按母型值进行归一化处理.

表2 蒸汽发生器重量优化设计结果Table 2 Optimal results of steam generator weight

优化后，一回路运行压力和传热管外径较母型有所减小，而传热管节径比增大，重量比母型减小了15.9%，优化效果显著.

2.2 冷凝器体积优化设计

在进行冷凝器体积优化设计时，基于独立性原则及一些工程可实现因素，本文选择冷却管外径dlo、冷却管节距sl、冷却水流速U和冷凝器压力Pl这4个参数作为优化变量，约束条件通常由工程和物理限制给定.从热力性能、结构强度等方面考虑，引入以下主要约束条件:冷却水阻Δpwater在一定范围内，冷凝液过冷度在Δtsub一定范围内，冷却管壁厚δ在一定范围内，冷凝器壳体长度L与宽度K比值在一定范围内;冷却管节距与冷却管外径比值sl/dlo在一定范围内.

冷凝器优化设计结果如表3所示，其中各参量都按母型值进行归一化处理.

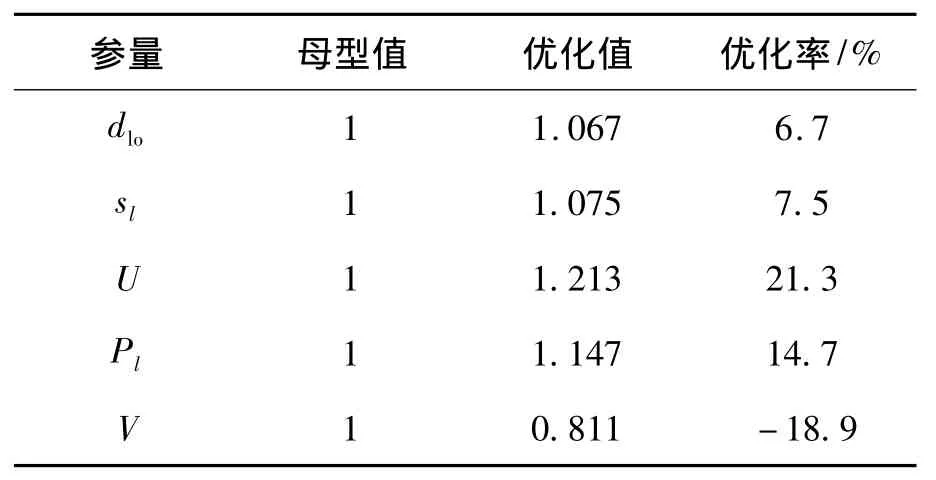
表3 冷凝器体积优化设计结果Table 3 Optimal results of condenser volume

在满足上述约束条件的情况下，优化后的4个优化变量都较母型有所增加，而冷凝器体积比母型值减小了18.9%.

3 结论

通过可行性判断规则处理约束，并引入复合形、改进复合形和遗传算法的交叉变异策略，设计了一种新型混合粒子群算法.利用复杂的标准测试函数，对该算法的有效性进行了验证，并将NHPSO算法应用在核动力设备优化设计上，取得了很好的优化效果，并得出以下结论:

1)改进混合粒子群能很好地处理多变量多约束的非线性约束优化问题，复合形和遗传算法的引入提高了标准粒子群算法的寻优能力.

2)对蒸汽发生器和冷凝器的优化设计表明，核动力设备有很大的优化空间，现有核动力设备的设计参数不是所有约束集合中的最优方案，在满足正常运行的约束条件下应用优化理论的思想，寻找优化变量的最佳匹配可减小核动力设备的重量和体积.

3)混合算法是优化算法的发展方向，算法还需要在处理多目标优化问题方面进行改进，以便核动力装置整体参数优化设计.

[1]KENNEDY J，EBERHART R C.Particle swarm optimization[C]//IEEE International Conference on Neural Networks.Perth，Anstralia，1995:1942-1948.

[2]PARSOPOULOS K E，VRAHATIS M N.Particle swarm op-timization method for constrained optimization problems[J].Artificial Intelligence，2002，3:603-607.

[3]DEB K.An efficient constraint handing method for genetic algorithms[J].Computer Methods in Applied Mechanics and Engineering，2000，186(2):311-338.

[4]焦巍，刘光斌，张艳红.求解约束优化的模拟退火PSO算法[J].系统工程与电子技术，2010，32(7):1532-1536.JIAO Wei， LIU Guangbin， ZHANG Yanhong. Particle swarm optimization based on simulated annealing for solving constrained optimization problems[J].Systems Engineering and Electronics，2010，32(7):1532-1536.

[5]顾宏杰，许力.利用带感知能力的粒子群算法求解约束优化问题[J].计算机应用，2011，31(1):85-88.GU Hongjie，XU Li.Perceptive particle swarm optimization algorithm for constrained optimization problems[J].Journal of Computer Applications，2011，31(1):85-88.

[6]VIEIRA D A G，ADRIANO R L S.KRÄHENBÜWL L，et al.Handling constraints as objectives in a multi-objective genetic based algorithm[J].Journal of Microwaves and Optoelectronics，2002，2(6):50-58.

[7]王福林，吴昌友，杨辉.用遗传算法求解约束优化问题时初始种群产生方法的探讨[J].东北农业大学学报，2004，35(5):608-611.WANG Fulin，WU Changyou，YANG Hui.Study on the productive method on the initial population by using genetic algorithm to solve the constrained optimization problem[J].Journal of Northeast Agricultural University，2004，35(5):608-611.

[8]LOVBJERG M，RASMUSSEN T K ，KRINK T.Hybrid particle swarm optimization with breeding and subpopulation[C]//IEEE International Conference on Evolutionary Computation.San Diego，USA，2000:1-6.

[9]HIGASHI N，IBA H.Particle swarm optimization with Gaussian mutation[C]//IEEE Proc of the IEEE Swarm Intelligence Symp.Indianapolis，USA，2003:72-79.

[10]王盟，王建军，贺士晶，等.一种解决复合形局部最优及加速计算的方法[J].计算机应用与软件，2011，28(2):277-278.WANG Meng，WANG Jianjun，HE Shijing，et al.An approach for solving complex local optimum and accelerating calculation [J].Computer Applications and Software，2011，28(2):277-278.

[11]RUNARSSON T P，YAO X.Ranking for constrained evolutionary optimization[J].IEEE Transactions on Evolutinary Computation，2000，4(3):284-294.

[12]COATH G，HALGAMUGE S K.A comparison of constraint-handling methods for the application of particle swarm optimization to constrained nonlinear optimization problems[C]//IEEE 2003 Congress on Evolutionary Computation.Ganberra，Australia，2003:2419-2425.

[13]PULIDO G T，COELLO C A C.A constraint-handling mechanism for particle swarm optimization[C]//IEEE 2004 Congress on Evolutionary Computation.Portland，USA，2004:1396-1403.

[14]马瑞新，刘宇，覃征，等.求解约束优化问题的动量粒子群算法[J].系统仿真学报，2010，22(11):2485-2488.MA Ruixin，LIU Yu，QIN Zheng，et al.Momentum particle swarm optimizer for constrained optimization[J].Journal of System Simulation，2010，22(11):2485-2488.

[15]秦慧敏，阎昌琪，王建军，等.立式自然循环蒸汽发生器的重量优化设计[J].原子能科学技术，2011，45(1):66-72.QIN Huimin，YAN Changqi，WANG Jianjun，et al.Optimal design of vertical circulation steam generator weight[J].Atomic Energy Science and Technology，2011，45(1):66-72.

[16]郑静，阎昌琪，王建军.核动力装置冷凝器体积的优化设计[J].原子能科学技术，2011，45(1):60-65.ZHENG Jing，YAN Changqi，WANG Jianjun.Optimal design of condenser volume in nuclear power plant[J].A-tomic Energy Science and Technology，2011，45(1):60-65.