四杆机构的三维CAD软件设计

张瑞东

(山西大学工程学院实习厂，山西 太原 030013)

平面四杆机构的设计方法主要有解析法、图解法和实验法。解析法的优点是精度高，但计算繁复;图解法的优点是易于理解、作图明确，但精度不如解析法高;实验法更加贴近于实际，实验法的过程中要用不同参数的物理机构模型通过反复实验求解机构尺寸，其模型的制作成本高、尺寸求解周期长。使用三维CAD软件的草绘、测量功能以及图解法的原理设计平面四杆机构，可将以上三种方法的优点组合于一体，以参数化及其内置函数功能创建虚拟机构草图并求解机构的尺寸。运用此方法可以使得平面四杆机构的设计既精确又高效，从而大大降低设计成本，提高经济效益。下面结合一个具体的实例来说明如何在三维CAD软件中使用图解法设计平面四杆机构。

1 脚踏轧棉机的设计条件及要求

设计脚踏轧棉机的曲柄摇杆机构，如图1所示。设计条件为踏板(即摇杆)在水平位置上下各摆 10°，且摇杆长度为 500mm，机架长度为1000mm。要求确定曲柄AB和连杆BC的长度，并计算此机构的最小传动角。

2 传统图解法的设计过程

传统的图解法使用尺规绘图及手工计算进行设计。根据上述已知的设计条件，踏板CD在水平位置上下摆动10°，就是曲柄摇杆机构中摇杆的极限位置，此时曲柄与连杆处于两次共线位置。取适当比例作图，作出两次极限位置AB1C1D和AB2C2D(见图2)。在图中直接量取曲柄和连杆的长度，可以得到:

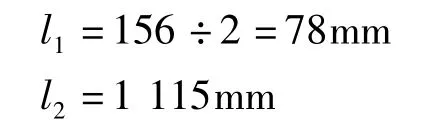
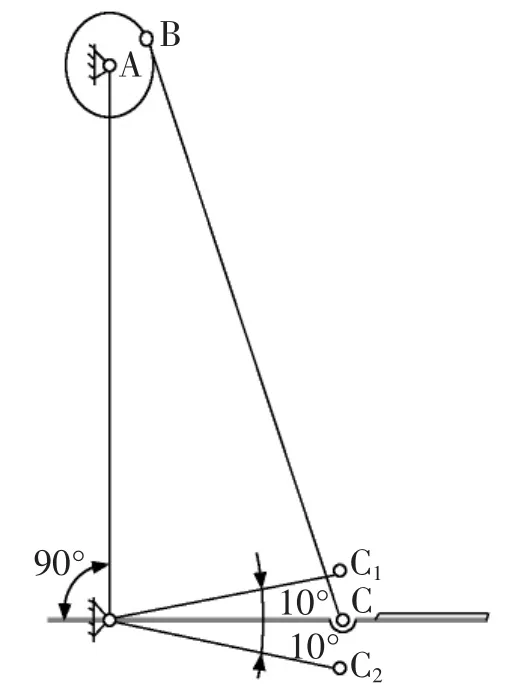
图1 设计条件

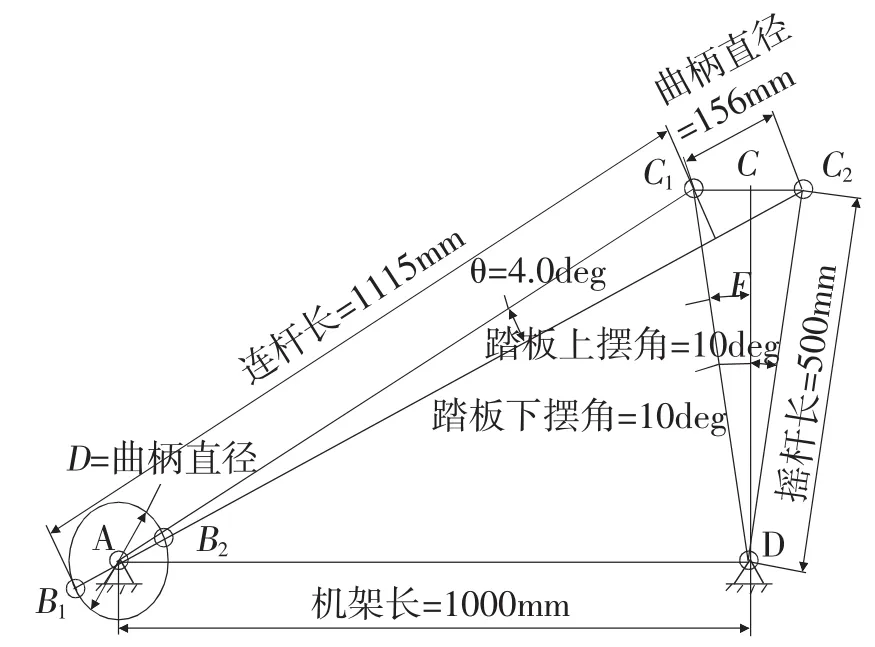
图2 使用尺规绘图绘制的设计图

因最小传动角位于曲柄与机架两次共线位置，因此取φ=0°和φ=180°代入传动角计算公式(2 －6)[1]计算可得:

由此可知最小传动角γmin=∠BCD=54.77°＞40°，设计结果可用。

3 使用解析法进行设计

根据图2可以看出，在曲柄与连杆的第一次共线位置时，∠ADC1=90°－10°=80°，因此在△ADC1中根据余弦定理可知

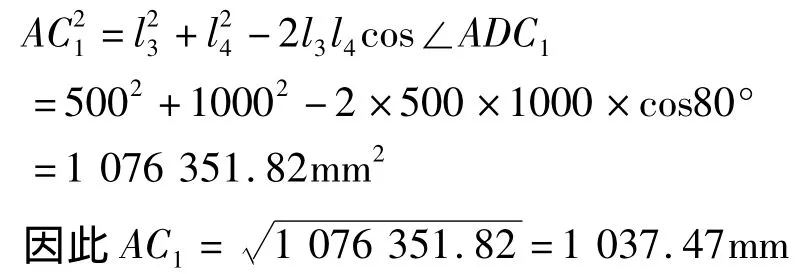
同理，在曲柄与连杆的第二次共线位置时，∠ADC2=90°+10°=100°，因此在△ADC2中根据余弦定理可知

因最小传动角位于曲柄与机架两次共线位置，因此取φ=0°和φ=180°代入传动角计算公式[1]计算可得:

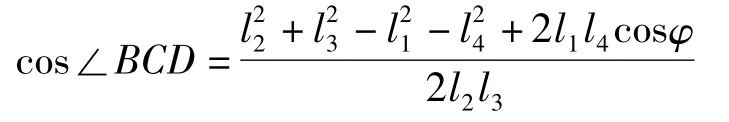
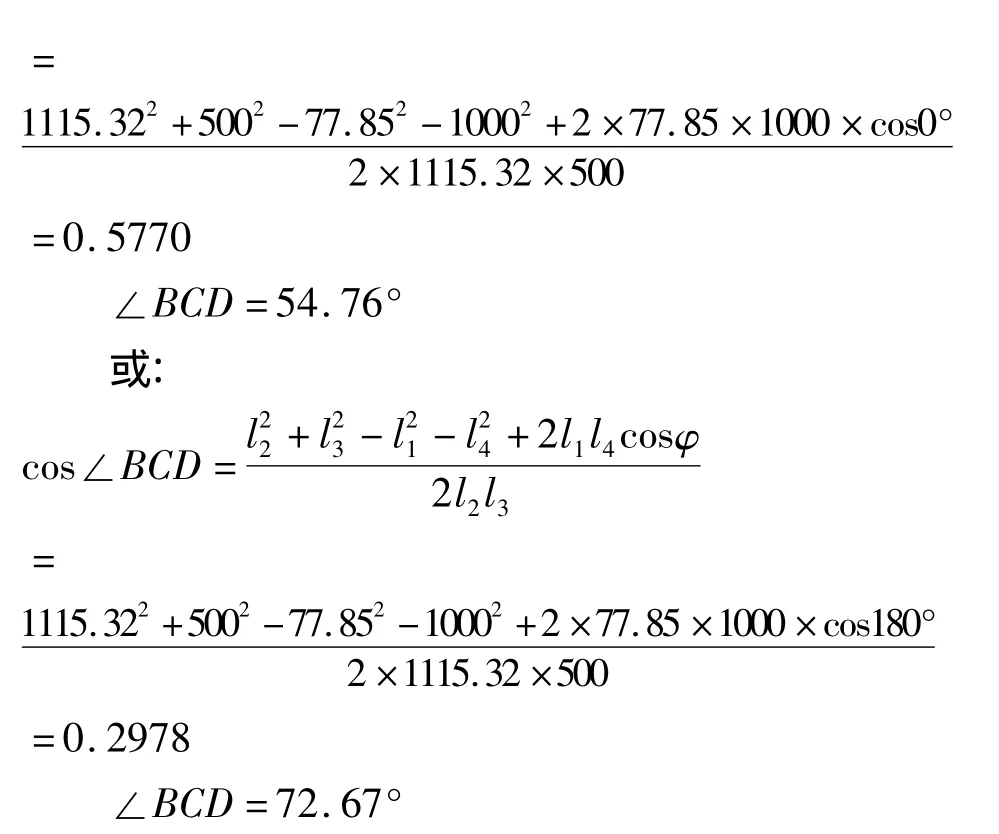
由此可知最小传动角γmin=∠BCD=54.76°＞40°，设计结果可用。

4 使用三维CAD软件进行设计

三维CAD软件Pro/E已经成为当今最为普及的3D CAD/CAM设计系统，是国内外多个家电、高科技、航天等领域知名企业首选的解决方案。参数化设计是Pro/E的重要特性之一。所谓的参数化设计，不仅是指根据具体的参数进行机构的设计，还指根据已知条件设计好机构后自动求解未知的参数[2]。在Pro/E中使用图解法进行设计并求解的详细步骤如下所述:

(1)启动Pro/E，并新建一个草绘;

(2)使用“线”工具画一条水平直线，长度为1000，该直线将作为曲柄摇杆机构的机架，直线的左右端点将分别作为曲柄和摇杆的旋转中心;

(3)使用“几何中心线”在机架的右端点画一条垂直的辅助线，然后使用“线”工具从摇杆的旋转中心画一条倾斜的直线，该直线的长度为500，与垂直辅助线的夹角为10°，该直线将作为曲柄摇杆机构中摇杆的一个位置;

(4)使用“镜像”工具做出与倾斜直线相对于垂直辅助线的对称直线，该直线将作为曲柄摇杆机构中摇杆的另一个位置;

(5)使用“几何中心线”过曲柄的旋转中心分别与两条倾斜直线的顶点相连，画出2条倾斜的辅助线，作为曲柄摇杆机构中曲柄与连杆2次共线位置的辅助直线，过左侧倾斜直线顶点的辅助直线称为C1辅助线，过右侧倾斜直线顶点的辅助直线称为C2辅助线;

(6)使用“线”工具过机架左端点沿着C1辅助线向下画一条较短的直线，再次使用“线”工具过机架左端点沿着C2辅助线向上画一条较短的直线，这两条直线将作为曲柄摇杆机构中摇杆处于两次极限位置时的曲柄。因为这2条直线是同一个构件的2次不同位置，所以这2条直线长度应该相等，使用约束中的“相等”工具使这2条直线长度相等。

(7)使用“线”工具在C1辅助线上连接曲柄的顶点和摇杆的顶点，再次使用“线”工具在C2辅助线上连接曲柄的顶点和摇杆的顶点，这两条直线将作为曲柄摇杆机构中摇杆处于两次极限位置时的连杆。因为这2条直线是同一个构件的2次不同位置，所以这2条直线长度应该相等，使用约束中的“相等”工具使这2条直线长度相等。现在曲柄摇杆机构的设计就全部完成了，屏幕上的图形代表的就是真实的机构，绘制完成的曲柄摇杆机构如图3所示。

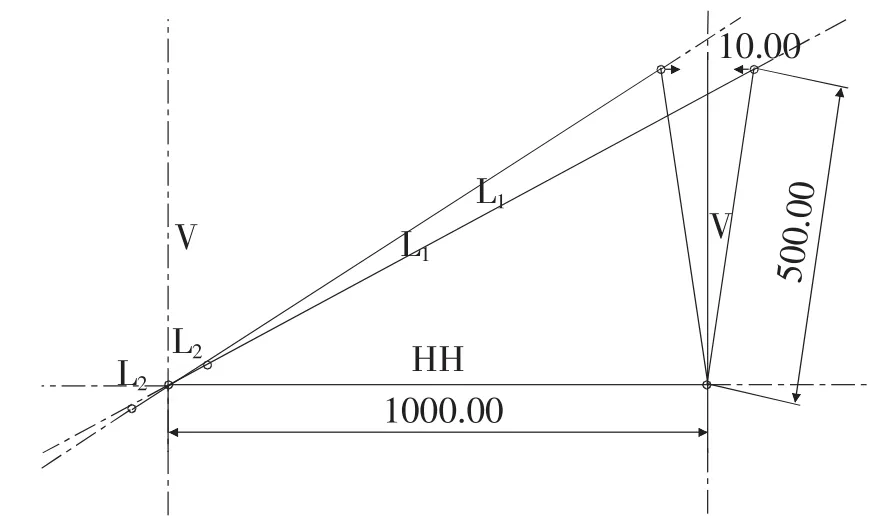
图3 使用三维CAD软件绘制的设计图

(8)测量曲柄和连杆的长度。使用“分析”菜单下的“距离”命令，分别选择曲柄和连杆的两个端点，在信息提示区显示出曲柄和摇杆的长度分别是77.8468mm 和 1115.3205mm。

(9)验算最小传动角。使用“分析”菜单下的“角度”命令，在曲柄与连杆的2次共线位置分别选择连杆和摇杆，在信息提示区显示出2个位置的传动角分别是 17.6655°和55.6263°。所以γmin=55.6263°＞40°，设计结果可用。

从以上过程可以看出，使用三维CAD软件的设计方法求解出的曲柄长度与连杆长度与使用解析法求解出的长度相比误差很小，而使用三维CAD软件的设计方法求解出的最小传动角与使用解析法求解出的最小传动角相比误差较大。这是由于三维CAD软件的圆并不是光滑曲线，而是用多个很短的直线模拟出的近似圆，因此圆弧所对的角度计算误差要比长度计算的误差大[2]。但是总体来看设计结果与解析法得出的设计结果基本相近，能满足工程设计的需要。使用三维CAD软件的设计方法与图解法、解析法相比较，过程简单，操作方便，结果比较精确。因此在工程设计领域应该大力推广这种设计方法，以逐步取代过程复杂、操作繁琐、手工计算较多的图解法和解析法。

5 结论

从本文可以看出，在三维CAD软件中通过图解法和自动计算进行设计，既使用了图解法设计的方便性，又得到了解析法设计的精确性。这种设计方法简便易行，并且能很容易地解决设计参数的调整和修改问题。总之，本文所介绍的设计方法能使用最简单的操作得到最确切的设计结果，既新颖又简洁，是对平面机构现有的设计方法、手段的扩展和补充，对提高平面机构设计工作的效率具有十分重要的意义。

[1]杨可桢.机械设计基础[M].北京:高等教育出版社，2006.

[2]林清安.Pro/ENGINEER野火3.0中文版基础零件设计[M].北京:电子工业出版社，2006.