基于伪门故障模型的PTM可靠度评估方法

卜登立

基于伪门故障模型的PTM可靠度评估方法

卜登立1,2

（1. 井冈山大学电子与信息工程学院，江西，吉安 343009；2. 同济大学软件学院，上海 201804）

为准确评价瞬时故障对电路可靠性的影响，通过将互连线故障建模在逻辑门的输入，建立伪门故障模型，并将之应用于基于Probability Transfer Matrix（PTM）的可靠度评估方法。在可靠度分析过程之中构建伪门并计算其PTM，从而计算出电路的PTM以及可靠度。通过对74系列电路和ISCAS85基准电路可靠度的计算验证了伪门故障模型以及基于伪门故障模型的PTM可靠度评估方法的有效性。

瞬时故障; 电路可靠度; 伪门故障模型; 概率转移矩阵

1 概述

随着工艺水平的发展，晶体管的特征尺寸不断减小[1-2]，由于电容降低，电路节点仅需很少的电荷来存储其状态；同时，器件工作电压也随工艺水平的发展有所下降，而为了降低功耗，设计者也会主动降低器件工作电压，相应的噪声容限也不断降低[1]。所有这些因素使得器件更容易受来自宇宙射线的高能粒子撞击、电容耦合、电磁干扰或电源瞬变[3-4]的影响，这些因素产生的瞬态脉冲导致电路节点状态发生翻转，从而产生瞬时故障，由于瞬态脉冲不会导致器件的永久损坏，因此也称之为软差错[3]。瞬时故障已经成为CMOS集成电路可靠度的重要威胁[5]，因此，业界对电路瞬时故障敏感度的关注度越来越高，可靠度已经成为非常重要的设计约束，有必要在设计过程中引入可靠度指标、评估工具，以便能够在设计阶段更好的集成和遵守这些约束[5]。

电路的可靠度是指电路在规定的条件下和规定的时间内完成规定功能的概率，传统上常用平均无故障时间来描述电路的可靠度。随着瞬时故障对电路可靠性的影响越来越严重，一般都采用概率分析方法来评价瞬时故障对电路可靠性的影响，并使用信号可靠度来表示电路的可靠度[6]。要在电路设计时评价瞬时故障对电路可靠性的影响，需要建立能够反映瞬时故障行为的概率模型，设计电路可靠性分析工具，分析电路对故障固有的屏蔽作用，从而定量地评价电路的可靠度，对电路设计进行指导，选择高可靠性设计或者对电路进行改进以提高电路的可靠度。近些年来，在门级对瞬时故障进行建模并进行可靠性分析受到了广泛关注，如基于PGM（Probabilistic Gate Model）的解析可靠度评估方法[7]、Single-Pass可靠度分析方法[8]、四态信号概率和Two-Pass可靠性分析方法[9]以及基于概率转移矩阵（Probability Transfer Matrix, PTM）的可靠度评估方法（简称为PTM可靠度评估方法）[10]，在这些方法中，PTM可靠度评估方法的评估结果最为准确[6-7,10]。

随着特征尺寸的减小，在制造过程中由于粒子入侵晶圆表面从而导致了电路中互连线的开路或短路缺陷[11]，另外随着互连线尺寸的收缩电迁移已成为互连线失效的主要原因，导致互连线间的短路或开路[7]，使得互连线的可靠度降低，因此在对逻辑电路进行可靠度评估时有必要考虑互连线故障的影响，并在门级建立能够描述互连线故障行为的故障模型。然而当前的PTM可靠度评估方法并没有考虑互连线的故障。本文考虑互连线故障对电路可靠度的影响，建立伪门（Pseudo Gate，PG）故障模型，将PG故障模型应用于PTM可靠度评估方法，使之除了能够分析逻辑门的故障对电路可靠度的影响之外，还可以分析电路中互连线的故障对电路可靠度的影响，并通过实验验证了PG故障模型以及基于PG故障模型的PTM可靠度评估方法的有效性。

2 PTM可靠度评估方法

PTM可靠度评估方法使用矩阵描述电路的行为，PTM用于描述电路的故障行为，理想转移矩阵（Ideal Transfer Matrix,）则描述电路的无故障行为，电路元件的/由真值表获得，整个电路的/根据电路元件的连接方式，采用张量积以及矩阵乘法计算获得。整个电路的对应于其真值表，描述了电路的功能，而/的计算过程则反映了电路的结构以及逻辑门对故障的固有屏蔽作用。下面对可靠度评估方法进行简要说明，更多关于可靠性评估方法的细节可以参考文献[6,10]。

2.1 电路PTM / ITM计算

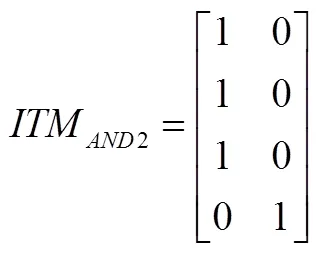
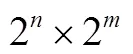
图1 示例电路C1

图1给出了一个具有3个PI，1个PO的示例电路C1，图中给出了该电路的分级情况，其的计算如式（3）所示。

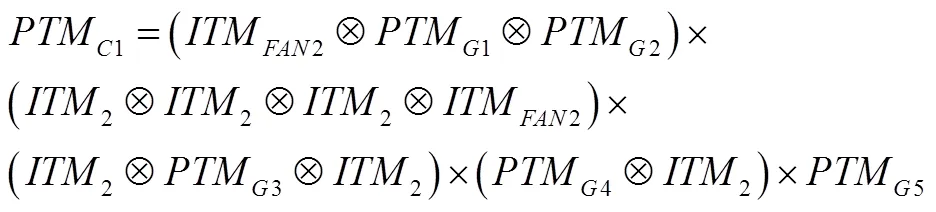
2.2 电路可靠度计算

通过上节所介绍的方式计算得到整个电路的和后，可按式（4）计算电路的可靠度。

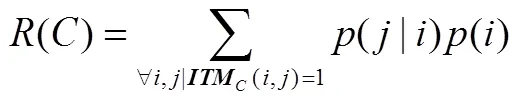
由于在电路输入数较多或者电路规模较大时，为求解电路的和，就算采用ADD存储和，依然不能很好解决存储空间过大的问题。为了降低时间和空间复杂度，文献[6]提出了对电路进行分割的方法，将规模较大的分级分割成若干模块，然后按照上述方法计算每个模块的可靠度，电路的可靠度则为各个模块可靠度的乘积。本文采用了文献[6]中的电路分割方法。

3 基于伪门故障模型的PTM可靠性评估方法

3.1 伪门故障模型

由于互连线连接电路中2个基本电路单元，互连线上发生的瞬时故障会对电路的可靠度产生影响，该影响可能是正面的，也可能是负面的，下面以图2为例进行说明。

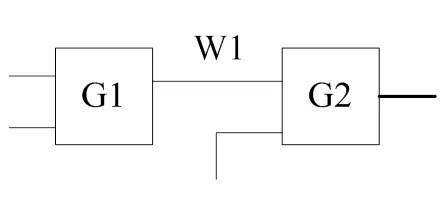
图2 互连线示意图

图2中的互连线W1连接两个逻辑门G1和G2，假设W1发生瞬时故障，如果G1的输出是正确的，则导致G2的输入发生差错；如果G1的输出是错误的，则由于W1发生了瞬时故障，使得G1的输出发生状态翻转，则导致G2的输入成为正确的输入，这体现了多故障的固有屏蔽作用。可见，互连线发生瞬时故障时，将对其所连接的后续单元的输入产生影响，如果将逻辑门的每个输入都看作一个单入单出的缓冲器或单元门，则可以将互连线的故障抽象为单元门的故障。将单元门和逻辑门作为一个PG，可以同时考虑出现在互连线以及逻辑门的瞬时故障，并采用概率分析方法来分析瞬时故障对电路可靠度的影响。图3给出一个2-输入与门的PG故障模型。

图3 输入与门PG故障模型

一个PG可看作是由若干个单元门（个数由逻辑门的输入数决定）和逻辑门构成，使用描述PG的故障行为，可先根据单元门和逻辑门的真值表分别构建单元门和逻辑门的，然后通过矩阵运算获得PG的；由于描述的是PG的无故障行为，因此PG的就是逻辑门的。

3.2 采用PG模型时电路可靠度的计算

本文将PG模型应用于PTM的电路可靠性评估方法，通过计算电路的PTM来计算电路的可靠度。采用PG模型需要对可靠度评估方法加以修改，在每一级电路的计算过程中构建PG并通过如式(6)所示的方式计算PG的。下面以图1所示电路C1为例说明采用PG模型时电路的计算，电路的分级以及PG的构建如图4所示。

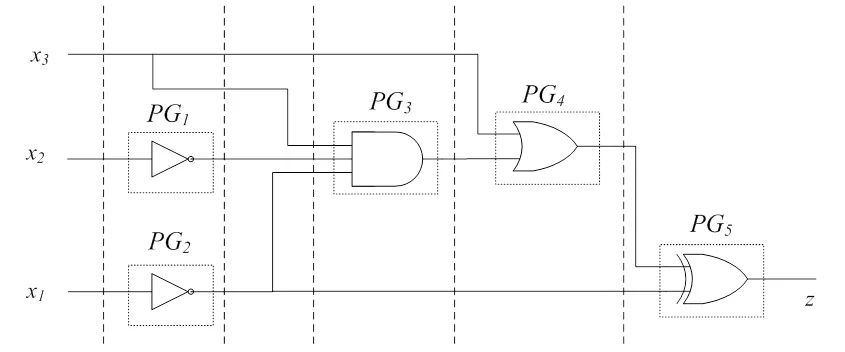
图4 电路C1的 PG构建

该电路共有5个逻辑门，因此需要构建5个PG，每一级的通过该级内电路元素的间的张量积计算得到，整个电路的则按照分级次序通过各级间的矩阵乘积计算得到。电路C1的的计算方法如式（7）所示。

由于已经将互连线的故障建模在PG中，此时的互连线可以看作是无故障的，因此在构建电路的的过程中，使用互连线的进行运算。整个电路的则和不采用PG模型时电路的计算方式完全相同。

在整个电路的以及计算出后，则可以使用式（4）来计算电路的可靠度。此时的计算结果则表示，在给定输入信号概率以及互连线和逻辑门故障概率的情况下，电路C的输出不发生错误的概率。

4 实验及结果分析

电路中各个门发生瞬时故障的概率可以根据物理实验结果、所处地理位置和海拔高度等信息进行估计，互连线发生瞬时故障的概率也可以根据版图敏感度、线宽、线高等信息进行估计。由于这些工作超出了本文的范围，因此本文在实施实验时对逻辑门以及互连线发生瞬时故障的概率进行适当假设，这也是当前的研究工作中普遍采取的方式。

基于PG故障模型的PTM可靠度评估方法使用C++实现，实验选取11个ISCAS85基准电路进行测试，程序运行的软件环境为Windows 7 Home Basic操作系统，硬件环境为CORE i3-2350 2.3GHz CPU 2GB RAM。实验结果如表1所示。

表1 电路可靠度评估实验结果

由实验结果可以看出，尽管存在着互连线、逻辑门以及电路结构的固有屏蔽作用，考虑互连线的故障后，电路的可靠度均有所下降，特别是当电路中的门数较多时，例如C3540、C5315、C6288和C7552，电路可靠度下降较为明显。这表明了将互连线故障建模在逻辑门的输入是合理的，同时也验证了PG模型的有效性。

另外，由于采用PG模型后，在可靠度评估过程中需要构建PG，因此电路可靠度评估的时间有所增加，但从实验结果来看，和不采用PG模型时的相比，对这些测试电路而言，平均时间开销为11.25%。

5 结束语

随着工艺水平的发展，晶体管的特征尺寸不断减小，器件工作电压和噪声容限也随之降低，互连线以及逻辑门对瞬时故障更加敏感，瞬时故障已经成为CMOS集成电路可靠度的重要威胁。为准确评估瞬时故障对电路可靠度的影响，本文通过将互连线故障建模在逻辑门的输入，建立了伪门模型，并将之应用于基于PTM的电路可靠性评估方法。PG模型非常灵活，对于互连线故障和逻辑门故障对电路的影响效果既可以独立分析，也可以综合考虑。实验结果表明，PG模型以及基于PG模型的电路可靠性评估方法是有效的。

[1] Smith K C, Wang A, Fujino L C. Through the Looking Glass - Trend tracking for ISSCC 2012[J]. IEEE Solid-State Circuits Magazine, 2012, 2: 4-20.

[2] Iwai H. Roadmap for 22 nm and beyond[J]. Microelectronic Engineering, 2009, 86: 1520-1528.

[3] Ramanarayanan R, Degalahal V, Krishnan R, et al. Modeling soft errors at the device and logic levels for combinational circuits [J]. IEEE Transactions on Dependable and Secure Computing, 2009, 6(3): 202-216.

[4] Miskov-Zivanov N, Marculescu D. A systematic approach to modeling and analysis of transient faults in logic circuits [C]. Proceedings of the 10th International Symposium on Quality of Electronic Design, San Jose, 2009: 408-413.

[5] Nicolaidis M. Soft errors in modern electronic systems [M]. New York: Springer, 2011: 1-3, 105-137.

[6] 王真, 江建慧. 基于概率转移矩阵的串行电路可靠度计算方法[J]. 电子学报, 2009, 37(2): 241-247.

[7] Han Jie, Chen Hao, Boykin E, et al. Reliability evaluation of logic circuits using probabilistic gate models [J]. Microelectronics Reliability, 2011, 51(2): 468-476.

[8] Choudhury M R, Mohanram K. Reliability analysis of logic circuits [J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2009, 28(3): 392-405.

[9] Franco D T, Vasconcelos M C, Naviner L, et al. Signal probability for reliability evaluation of logic circuits [J]. Microelectronics Reliability, 2008, 48(8-9): 1586-1591.

[10] Krishnaswamy S, Viamontes G F, Markov I L, et al. Probabilistic transfer matrices in symbolic reliability analysis of logic circuits [J]. ACM Transactions on Design Automation of Electronic Systems, 2008, 13(1): 8:1-8:35.

CIRCUIT RELIABILITY EVALUATION BASED ON PSEUDO-GATE MODEL

BU Deng-li1,2

（1. School of Electronics and Information Engineering, Jinggangshan University, Ji’an, Jiangxi 343009, China;2. School of Software Engineering, Tongji University, Shanghai 201804, China）

To evaluate accurately the impact of transient fault in logic circuit, a pseudo-gate (PG) model is proposed through modeling interconnection fault at the input of logic gate, and applied in probability transfer matrix (PTM) based circuit reliability evaluation method. PG is constructed and its PTM is computed in the process of reliability evaluation, in this way the circuit PTM is obtained and the circuit reliability is calculated. The effectiveness of PG model based reliability evaluation method is validated by computing the reliability of ISCAS85 benchmark circuits.

transient fault; circuit reliability; pseudo-gate fault model; probability transfer matrix

TP331，TP202+.1

A

10.3969/j.issn.1674-8085.2012.05.013

1674-8085(2012)06-0056-05

2012-04-12；

2012-09-24

卜登立(1975-)，男，河北定州人，副教授，博士生，主要从事VLSI设计和可靠性评估，嵌入式计算等研究(E-mail: bodengli@163.com).