两类映射的近似耦合不动点定理

贾必伟，仇秋生

两类映射的近似耦合不动点定理

*贾必伟，仇秋生

(浙江师范大学数学系，浙江，金华 321004)

在度量空间中，讨论了近似耦合不动点存在性问题。首先研究了广义非扩张型映象的近似耦合不动点。作为应用，获得了赋范空间中有界集上的非扩张映象的近似耦合不动点。其次在半序度量空间中讨论了非连续混合单调算子的近似耦合不动点存在定理。

近似耦合不动点；非扩张映象；混合单调算子

非扩张映象是Banach压缩映象的一种自然的推广，这种映象在近代许多数学分支，其中特别是在非线性半群，遍历理论和单调算子理论有许多重要的应用。关于非扩张映象不动点理论Marr[1]得出著名的Kaku tani-Markov不动点定理的一些推广；Lim[2]证明了在一致凸Banach空间集值非扩张映象不动点的存在性；Kirk和Massa[3]将Lim’s的结果推广到Banach空间，其中要求Banach空间的有界闭凸子集的一个有界序列的渐进中心是非空紧的；Lan和Zhang[4]研究了定义在Banach空间(或广义局部凸空间) 弱紧凸子集上的半群非扩张映象的不动点性质。众所周知，单调迭代技术在处理许多非线性问题时起着至关重要的作用。这类技术与混合单调算子不动点有密切的联系。半序Banach空间中单值混合单调算子不动点定理已有广泛研究[5-7]；最近，集值混合单调算子不动点定理被许多作者关注[8-9]；其中文献[8]，在半序Banach空间讨论了集值混合单调算子的耦合不动点的存在和逼近问题，其中算子要求满足稠密条件且上半连续；Laksh和Ciric[10]在完备半序度量空间证明了连续混合单调非线性压缩映象的耦合不动点定理；而后Karapinar[11]将其推广到完备锥度量空间，其中锥为正则锥。

1 预备知识

则称具有近似耦合不动点性质。

则具有近似耦合不动点性质。

即

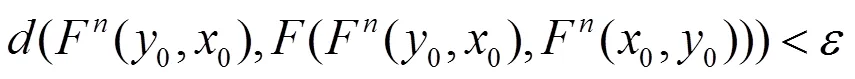
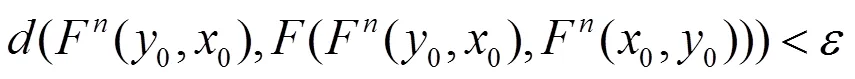
2 非扩张映射的近似耦合不动点定理

一般的，有

则具有近似耦合不动点性质。

由 (2) ，有

于是满足条件(1)。

使得

则

同理有

则具有近似耦合不动点性质。

注2.1：非扩张映象不一定有不动点，但当为有界集时，非扩张映象

有近似耦合不动点。

下面定理及推论证明了Kannan型非扩张映象在为有界集的情况下，存在近似耦合不动点。

则

类似于定理2.2 的证明，由定理2.3 可得下列推论。

,

又

所有患者每6个月进行1次电话随访，末次随访日期为2018-02-28。随访时间 5～50个月，中位随访时间32.1个月,期间有36例患者复发，13例患者死亡。复发转移要求有病理诊断或者典型的影像学及临床表现，复发和生存时间按月记录，以手术日至患者复发、死亡或最后一次就诊(随访)时间为复发或生存期限。失访，非肿瘤死亡及截止点生存病例按统计分析要求列为截尾数据处理。

故

。 类似定理2.3 证明，有 由引理1.1 得，，。 推论2.2 设E为一赋范空间，为有界集，映射满足非扩张条件： ， 则具有近似耦合不动点性质。 3 混合单调算子的近似耦合不动点 定义3.1[11] 设为一个半序集，映射，，称具有混合单调性质，若， 。 定义3.2 (X,d)为度量空间，映射 ， ， ，若 称F关于g具有近似耦合不动点性质。 定义3.3 [11] ，映射，，称映射F与g为互换的，如果 BY-4型纳米陶瓷基高温防氧化涂层材料对铝电解用碳素阳极的抗氧化应用 李顺华，王博一，杨国荣，等 4 73 表现器乐本身就是一种对美的探索与表现的过程。学习乐器技能时，教师应不拘一格、灵活多样的指导学生学习，避免单调乏味的纯技术训练，通过多样教学将器乐技巧融于课堂教学中，提升教学实效。 , 。 定理3.1 (1)设，为一个半序集，(X,d)为度量空间；(2) ，满足，且；(3)F:X×X→X，，F具有混合g-单调性质，满足下列条件： (i)对所有满足，的，有 ； (ii)，F与g互换； (iii) 存在，使 ， ，则 ， 。 证明 由条件 (iii) ，存在，使，。 又由于，构造序列，满足，。 下证序列，为单调序列。利用数学归纳法，当时，由， 及 ， 得 ， 。 假设， 成立，由F具有混合单调性质有 2018年三季度，在二、四季度“618”、国庆、双十一等促销节点的前后挤压下，部分消费需求被分流，叠加宏观经济环境变化和房地产市场调控的影响，家电市场整体表现不尽人意。然而分品类来看，依然有一些亮点呈现，比如生活电器的高速增长，冰洗市场的结构升级成效正在凸显。 故对所有 ， ， 成立。令 由于 则 同理。 11月16日凌晨，巴陵石化煤化工部仪表车间合成班值班员蒋正流接到合成车间工艺四班人员报告后，立即赶往合成总控制室。“我们询问了各运行部，都没有同类型的冗余通讯卡备件。询问备件厂家，他们答复从北京邮寄，最快也要两天。”仪表车间主任姜文伟说。 从而有。 又当时，，则 则为单调递减序列，那么存在，有。 有关传承人的界定，各国的确定标准和程序大有不同，非物质文化遗产法就对我国代表性传承人的认定标准作出了清晰的规范和界定。目前的认定标准是：首先继承者应当精通并能驾驭其继承的属于非物质文化遗产的技艺技能；其次他们还应当在某些特别的地域中拥有较大的知名度和感染力并且具有象征性；最后还应当踊跃地发展和传播与承继相关的活动和事业。而关于认定程序，要严格根据相关法律法规对国家级象征性项目的规定认真审批，并向社会公布通过认定的具有代表性的传承人的名单。 假设，考虑到，，则由 两边取极限 有 结合描述性统计分析，532家样本企业中成功获取银行贷款的为480家，贷款利率平均上浮71.4%，抵押贷款笔数占比为68.1%。样本企业中22.1%的小微企业选择向五大商业银行申请贷款，77.9%的企业选择向股份制商业银行、城市商业银行等申请贷款。从负债率来看，小微企业的整体负债水平较低，均值为38.65%，平均年销售收入为3 280万元。关系深度(rela_de)均值为0.751，表明大多数小微企业倾向于选择其主要关系银行作为贷款申请对象；平均关系年限仅为2.79年，这与大多数小微企业为初创型、成立年限较短有关。 矛盾。 从而有，即 则，，，有。 即 ， 。 同理 ， 。 令， 则有 同理。 从而，。 注3.1：令 ，，得到推论3.1。 推论3.1 设，为一个半序集，(X,d)为度量空间，映射，，F具有混合g-单调性质，满足： (i)对所有满足，的，存在，使 ； (ii) ，F与g互换； (iii) 存在，使 ， ，则 ， 。 注3.2：当，立即得到下述推论。 推论3.2 设为一个半序集，(X,d)为度量空间，映射为混合单调算子，满足： (i) 对所有满足, 的，存在，使 ； (ii) 存在，使， ，则 ， 。 参考文献： [1] DeMarr R. Common fixed points for commuting contractions[J]. Pacific J. Math, 1963, 13: 1139-1141. [2] Lim T C. A fixed point theorem for multivalued non-expansive mappings in a uniformly convex Banach space[J]. Bull. Amer. Math. Soc, 1974, 80: 1123-1126. [3] Kirk W A, Massa S. Remarks on asymptotic and Chebyshev centers[J]. HoustonJ. Math, 1990, 16(3): 357-364. [4] Liu A T, Zhang M Y. Fixed point properties of semi-groups of non-expansive mappings[J].Journal of Functional Analysis, 2008, 254: 2534-2554. [5] Wu Y S, Li G Z. On the fixed point existence and uniqueness theorems of mixed monotone operators and their applications[J]. Acta. Math. Sci, 2003, 46: 161-166 (in Chinese). [6] Zhang Z T. New fixed point theorems of mixed monotone operators and applications[J]. J. Math. Anal. Appl, 1996, 204: 307-319. [7] Gun D, Lakshmikantham V. Coupled fixed points of nonlinear monotone operators with applications[J]. Nonlinear. Anal, 1987, 11: 623-632. [8] Huy N B, Khanh N H. Fixed point for multivalued increasing operators[J]. J. Math. Anal. Appl, 2000, 250: 368-371. [9] Hong S H. Fixed points of discontinuous multivalued increasing operators in Banach spaces with applications[J]. J. Math. Anal. Appl, 2003, 282: 151-162. [10] Laksh V, Ciric L. Couple fixed point theorems for nonlinear contractions in partially ordered metric spaces[J]. Nonlinear. Anal, 2009, 70: 4341-4349. [11] Karapinar E. Couple fixed point theorems for nonlinear contractions in cone metric spaces[J]. Comp. Math. Appl, 2010, 59: 3656-3668. [12] Cromme L J, Diener I. Fixed point theorems for discontinuous mapping[J]. Math. Programming(ser.A) 1991, 51(2):257-267. [13] Hou S H, Ya C G. Approximate fixed points for discontinuous set-valued mappings[J]. Math. Meth. Oper, Res,1998, 48: 201-206 . [14] Tijs S, Torre A, R Branzei. Approximate fixed point theorems[J]. Libertas Math,2003, 23:35-39. [15] Branzei R, J Morgan, V Scalzo, et al. Approximate fixed point theorems in Banach spaces with application in game theory[J]. J. Math. Anal. Appl, 2003, 285:619-628. [16] Berinde M. Approximate fixed point theorems[J]. Stud. Univ. “Babes, Bolyai”, Math, 2006, 51(1):11-25. [17] Prasad B, Singh B, Sahni R. Some approximate fixed point theorems[J]. Int. Journal of Math. Analysis, 2009, 3(5):203-210. [18] 张石生. 不动点理论及应用[M].重庆：重庆出版社,1984. APPROXIMATE COUPLE FIXED POINT THEOREMS FOR TWO KINDS OF MAPPINGS *JIA Bi-wei, QIU Qiu-sheng (Department of Mathematics，Zhejiang Normal University，Jinhua，Zhejiang 321004, China) Abstract: In this paper, the existence problems of approximate couple fixed point are discussed on metric spaces. Firstly, the approximate couple fixed points of generalized non-expansive mappings are studied. As application, the approximate couple fixed points of non-expansive mappings in the bounded sets of normed spaces are obtained. Secondly, the existence theorems of the discontinuous mixed monotone operators in the partially ordered metric spaces are discussed. Key words: approximate couple fixed point; non-expansive mapping; mixed monotone operator 中图分类号：O177.91 文献标识码：A DOI:10.3969/j.issn.1674-8085.2012.06.002 文章编号：1674-8085(2012)06-0006-06 收稿日期：2012-06-23； 修改日期：2012-09-18 基金项目：浙江省自然科学基金项目(Ly12A01005) 作者简介：*贾必伟(1987-)，女，江苏淮安人，硕士生，主要从事最优化理论研究(E-mail: xiaxuejiabiwei@163.com); 仇秋生(1962-)，男，江西上高人，教授，博士，主要从事非线性泛函分析与向量优化理论研究(E-mail: qsqiu@zjnu.cn).