分数阶微分方程积分边值问题正解的存在性

王 林，张兴秋

分数阶微分方程积分边值问题正解的存在性

*王 林，张兴秋

（聊城大学数学科学学院，山东，聊城 252059）

利用不动点指数理论在相应线性算子的第一特征值条件下，得到一类分数阶微分方程积分边值问题正解的存在性定理。

分数阶微分方程；积分边值问题；第一特征值；正解；不动点指数

近年来，分数阶微分方程成为人们研究的热点，其广泛应用于数学、流体力学、流变学、粘弹性力学等诸多学科。其中许多数学工作者对分数阶微分方程解的存在性做了大量研究[1-10]。

在文献[1]中，王永庆等在Banach空间研究分数阶微分方程

在文献[4]中，李等研究分数阶微分方程

在文献[10]中，白等研究分数阶微分方程

目前，结合第一特征值研究分数阶微分方程积分边值问题正解存在性的结果较少。

本文利用不动点指数理论结合相应线性算子的第一特征值研究下面的分数阶微分方程积分边值问题正解的存在性。

1 预备知识

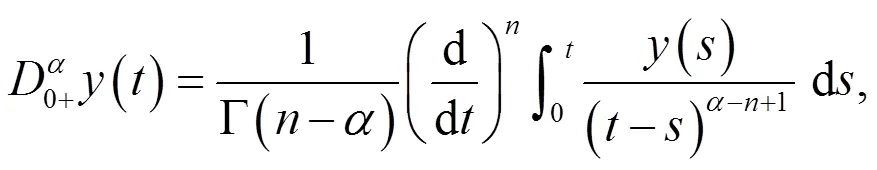
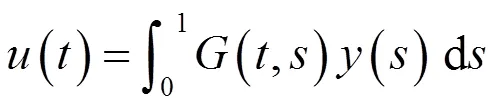
其中

证 应用引理1.2，将(1)中微分方程转化为等价的积分方程

因此得到

将(1.3)式从0到1积分得

得

因此，

证毕。

证毕。

.

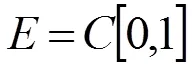
定义

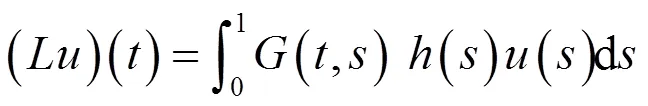
由Krein-Rutmann定理，引入下面的引理。

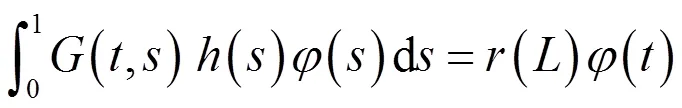
2 主要结果及其证明

定理2.1设

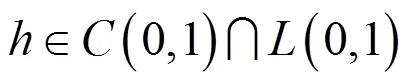
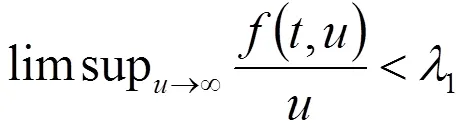
则边值问题(1)至少有一个正解。

我们断言

下面证明是有界的。

则是有界的。

由引理1.9知

由(2.3)、(2.6) 得

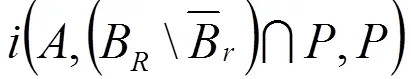
证毕。

[1] 王永庆, 刘立山. Banach空间中分数阶微分方程点边值问题的正解[J]. 数学物理学报, 2012(32):246-256.

[2] Xu Xiaojie, Jiang Daqing, Yuan Chengjun. Multiple positive solutions for the boundary value problem of a nonlinear fractional differential equation[J]. Nonlinear Analysis, 2009(71): 4676-4688.

[3] Bai Zhanbing. On positive solutions of a nonlocal fractional boundary value problem [J]. Nonlinear Analysis, 2010 (72):916-924.

[4] Li C F, Luo X N, Yong Zhou. Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations[J]. Computers and Mathematics with Applications, 2010(59):1363-1375.

[5] Zhao Yige, Sun Shurong, Han Zhenlai, et al. The existence of multiple positive solutions for boundary value problems of nonlinear fractional differential equations[J]. Commun Nonlinear Sci Numer Simulat, 2011(16):2086-2097.

[6] Christopher S Goodrich. Existence of a positive solution to a class of fractional differential equations[J]. Applied Mathematics Letters, 2010(23):1050-1055.

[7] Wang Yongqing, Liu Lishan, Wu Yonghong. Positive solutions for a nonlocal fractional differential equation[J]. Nonlinear Analysis, 2011(74):3599-3605.

[8] Babakhani A, Varsha Daftardar-Gejji. Existence of positive solutions of nonlinear fractional differential equations[J]. J. Math. Anal. Appl., 2003(278) :434-442.

[9] Zhao Yige, Sun Shurong, Han Zhenlai, et al. Positive solutions for boundary value problems of nonlinear fractional differential equations[J].Applied Mathematics and Computation,2011(217):6950-6958.

[10] Bai Zhanbing, LüHaishen. Positive solutions for boundary value problem of nonlinear fractional differential equation[J]. J. Math. Anal. Appl.，2005(311): 495-505.

[11] Guo D, Lakshmikantham V. Nonlinear problems in abstract cones[M]. New York :Academic Press, 1988.

[12] 郭大钧. 非线性泛函分析[M]. 济南:山东科学技术出版社, 2004.

EXISTENCE OF POSITIVE SOLUTIONS FOR A CLASS OF FRACTIONAL DIFFERENTIAL EQUATIONS WITH INTEGRAL BOUNDARY VALUE PROBLEM

*WANG Lin，ZHANG Xing-qiu

(Department of Mathematics, Liaocheng University ,Liaocheng , Shangdong 252059, China )

In this paper, we are concerned with the existence of positive solutions for a class of fractional differential equations with integral boundary value problem. Furthermore, we obtain the existence of positive solutions by fixed point index theory under some conditions concerning the first eigenvalue with respect to the relevant linear operator.

fractional differential equations; integral boundary problem; the first eigenvalue; positive solution; fixed point index

O175.8

A

10.3969/j.issn.1674-8085.2012.06.001

1674-8085(2012)06-0001-05

2012-06-12；

2012-07-28

国家自然科学基金项目（10971179）；山东省优秀中青年科学家奖励基金项目(BS2010SF004)；山东省高等学校科技发展计划项目(J10LA53)

*王 林(1985-)，男，山东茌平人，硕士生，主要从事非线性系统理论及应用研究(E-mail:15020608675@163.com);

张兴秋(1975-)，男，山东济宁人，副教授，博士，主要从事微分方程理论及应用研究(E-mail:zhxq197508@163.com).