浅谈如何打开解单物体多过程题的门

◆过小英

(杭州市长河高级中学)

浅谈如何打开解单物体多过程题的门

◆过小英

(杭州市长河高级中学)

单物体多过程题是近几年高考的一个热点，主要考查学生的综合分析能力。学生对这类题的得分率较低，很大一部分原因是没有找到解题的突破口——衔接态。本文从多方面入手分析如何突破衔接态问题，提高学生解单物体多过程题的能力。

单物体多过程题 综合分析能力 衔接态问题

单物体多过程题，通常是指一个物体连续完成多个运动，要求学生求某个运动物理量或某个力等。单个物体多个运动过程问题是近几年浙江高考的一个热点，从前几年的高考统计来看，得分率都不是很理想，甚至可以说很低。再结合自己学校各次模拟考试这类题学生的得分情况来看，学生对这类题目的得分都不高，出乎老师的意料。之所以学生会出现这种情况，主要是学生没有理解单物体多过程题的衔接态。所谓衔接态就是指两种运动交接的状态。

一、分析物体的受力以突破衔接态

上题中，碰撞结束的瞬间C所在处即为衔接态，第二问问C是否立即做圆周运动，那就首先对C状态进行受力分析，发现绳子拉力为零，C受到竖直向上的___N_恒定不变的力，与此时速度方向刚好垂直，这恰好是类平抛运动的受力与运动的特征，由此想到C接下去做的是类平抛运动，再采用类平抛的解题方法“化曲为直”求解此题。

二、挖屈隐含运动以突破衔接态

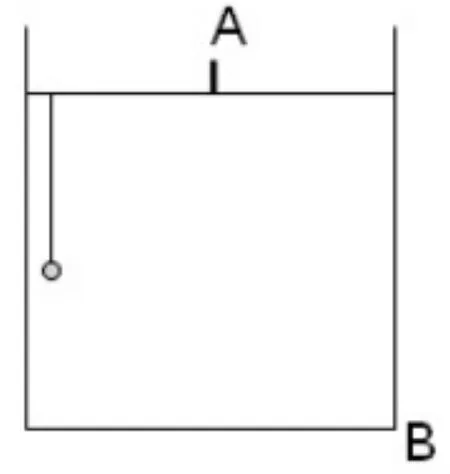
如图所示，长为L的细绳上端系一质量不计的环，环套在光滑水平杆上，在细线的下端吊一个质量为m的铁球(可视作质点)，球离地的高度h=L，当绳受到大小为3mg的拉力时就会断裂。现让环与球一起以的速度向右运动，在A处环被挡住而立即停止，A离右墙的水平距离也为L，不计空气阻力，已知当地的重力加速度为g，试求:在环被挡住而立即停止时绳对小球的拉力大小。在以后的运动过程中，球的第一次碰撞点离墙角B点的距离是多少?

环被挡住立即停止的瞬间，是从匀速直线运动转到平抛运动的衔接态，这是大部分学生所能认识到，再根据拉力等于重力，可见绳子不会断掉，思路到此断了，解题无门。其实在环被挡住的瞬间“看似风平浪静，实则暗波涌动”，分析小球的力与运动，可知小球应该是做圆周运动，绳子的拉力突变为3mg，刚好把绳子拉断，然后才是平抛运动的开始，所以虽然是同一个点，但是应该分析出小球隐含着的运动变化，只有分析出这一点才能准确求解此题。

三、关注机械能变化以突破衔接态

例如上一题，再加第三问:绳子再次绷紧后小球做什么运动，最大速度为多少?再次绷紧处即为衔接态。很大一部分学生能回答出小球接下去做圆周运动，最大速度出现在最高点，因为是变速圆周运动，所以想到用动能定理来解，由前面的类平抛运动可求得绳子再次绷紧时的速度，此为初速度，最高点的速度为末速度，这个过程电场力做正功，重力做负功，根据动能定理列方程求出末速度。之所以出现这样的错解是因为在绳子再次绷紧这个衔接态没有进行机械能是否守恒的分析:圆周运动的速度是沿圆周的切线的，而类平抛运动的末状态的速度并没有沿圆周的切线，这里机械能有损失:沿绳子方向的速度对应的动能损失。同样问题也存在在下图的情景中:

图1:绳子一端固定，另一端连着一小球A，把小球A水平仍出，求小球A到最底点时的速度。小球从平抛运动转到圆周运动的衔接态机械能有损失。

图2:B球放手，最后经过A点，求过A点的速度。小球从自由落体运动转为圆周运动的衔接态机械能有损失(图3的C点为速度分析:V1对应的机械能损失)。

四、理想化处理实际问题以突破衔接态

如图所示，一只海豚从与水平面齐平的礁石上竖直跃起，重心上升的最大高度为h=1.0m;然后，竖直落入水中，随水自由漂游，海豚的质量为m=100kg，体积为 V=0.125m3，水的流速为 vx=4m/s，水密度取 =1.0 ×103kg/m3，不计空气阻力和水的粘滞阻力，并认为海豚在水中受到的浮力恒定不变。试计算:

(1)海豚从礁石上跃起做了多少功?跃起的初速度有多大?

(2)海豚下沉的最大深度是多少?

(3)海豚第一次入水点与第一次出水点的水平距离是多少?

这一题，大部分学生都能分析出海豚先做竖直上抛运动，全部入水后又做匀减速直线运动，但是在海豚入水的过程中，考虑到海豚受到的浮力在不断改变，那就是一个变加速直线运动(竖直方向)，所以大部分学生只能得第一小问的分数。其实对比海豚入水所用的时间与海豚完全入水向下匀减速再向上匀加速出水的时间，不难发现入水所用时间完全可以忽略不计，这样竖直方向海豚的运动就是入水前的上抛运动和入水后的类上抛运动，水平方向匀速直线运动，后两问的得分就不成问题了。

总之，衔接态是前一种运动的末状态，是后一种运动的初状态，突破衔接态往往就打开了解单物体多过程题的门。