论数控机床对刀原理及其实质

2012-10-24杨绍奎

制造技术与机床 2012年11期

杨绍奎

（中山火炬职业技术学院，广东中山 528436）

长期以来，从出版的教科书和发表的论文来看，关于数控机床的对刀原理及其实质的阐述一直存在错误，集中体现在“对刀就是测量工件原点在机床坐标系的坐标”或者“对刀就是测量刀具刀位点在工件坐标系中的坐标”等错误的阐述或解释。幸运的是在数控编程传授中这种错误解释并不影响对刀的正确操作，但是对于学习者正确理解对刀原理以及数控系统对刀具的控制方式和深刻理解各种对刀操作有误导作用，造成教授者解释不清，学习者难于明白的局面。其实，数控系统在对刀时并没有测量工件原点（W点）在机床坐标系的坐标，也没有测量刀具刀位点（T点）在工件坐标系中的坐标。

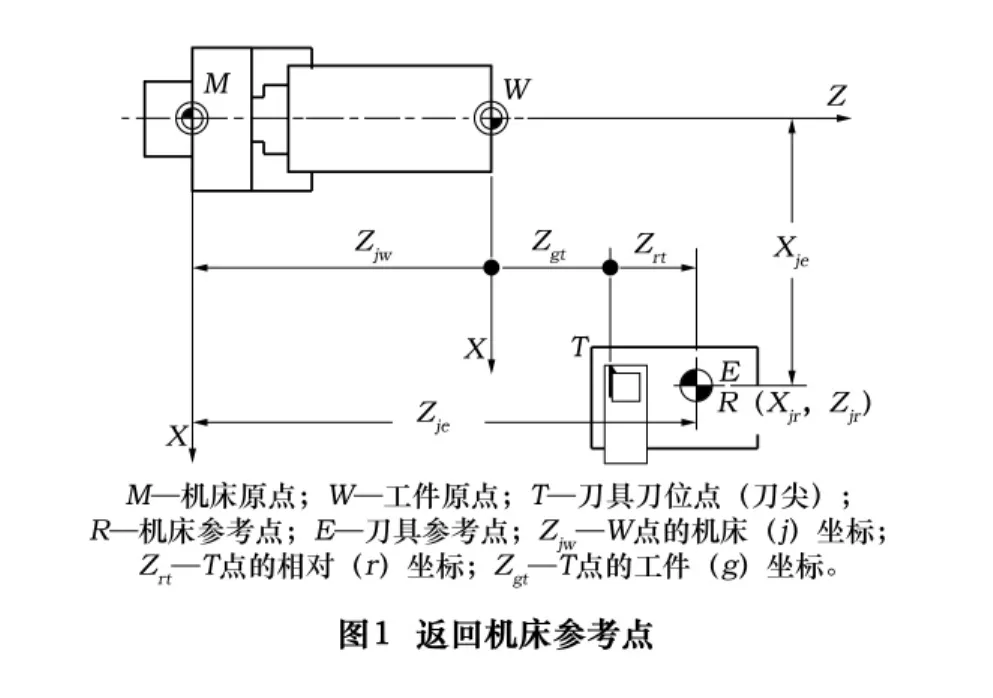
以数控车床为例来说明，在图1所示数控车床返回机床参考点（R点）时，数控系统通过传感器捕捉R点，并使用预置在系统内部的R点机床坐标（Xjr，Zjr）建立机床坐标系MXZ，并同时显示系统控制的机床坐标。系统控制的机床坐标不是R点的坐标（因R点是固定的），而是刀具参考点即E点的机床坐标（E点是机床返回到R点时刀架内或刀架延伸部分内与R点重合的那一个点），所以E点的机床坐标（Xje，Zje）被监视。安装工件和刀具后，从图1可知:

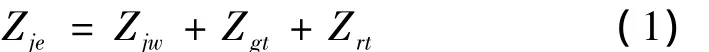
式中:Zjw和Zrt是不变的未知量，很显然无法从1个方程式中解出2个未知量，也就是说数控系统虽然建立了机床坐标基准MXZ，但却无法知道或测量W点的机床坐标Zjw。T点的工件坐标Zgt是可以测量的，但数控系统仅测量它是没有意义的。在FANUC系统等编程或操作说明书中阐述了对刀方法，但没有阐述其原理，这正是本文要阐述的。

1 数控系统内建的坐标系

1．1 机床坐标系和机床参考点

机床坐标系是系统内建的第一个坐标参照系统，其坐标原点称为机床原点，也叫M点;该坐标系中的坐标以“机床坐标”的形式在CRT上显示。机床坐标系是一个固定的坐标系（用户不能移动或改变M点的位置），机床坐标系的建立为数控机床的运动控制提供了统一且唯一的参照基准。

机床参考点也叫R点，R点在机床上是固定的，其机床坐标（Xjr，Zjr）预置在CNC系统内;在称为“返回机床参考点”的操作过程中，CNC通过传感器精确定位R点后并调用R点的机床坐标（Xjr，Zjr）建立机床坐标系MXZ，见图1。

1．2 相对坐标系和刀具参考点（运动控制点）

在R点建立机床坐标系后，数控系统还以R点为原点内建了另一个浮动的坐标参照系统，称为相对坐标系，如图2中的RXZ，其坐标原点称为相对原点。该坐标系中的坐标以“相对坐标”的形式在CRT上显示。

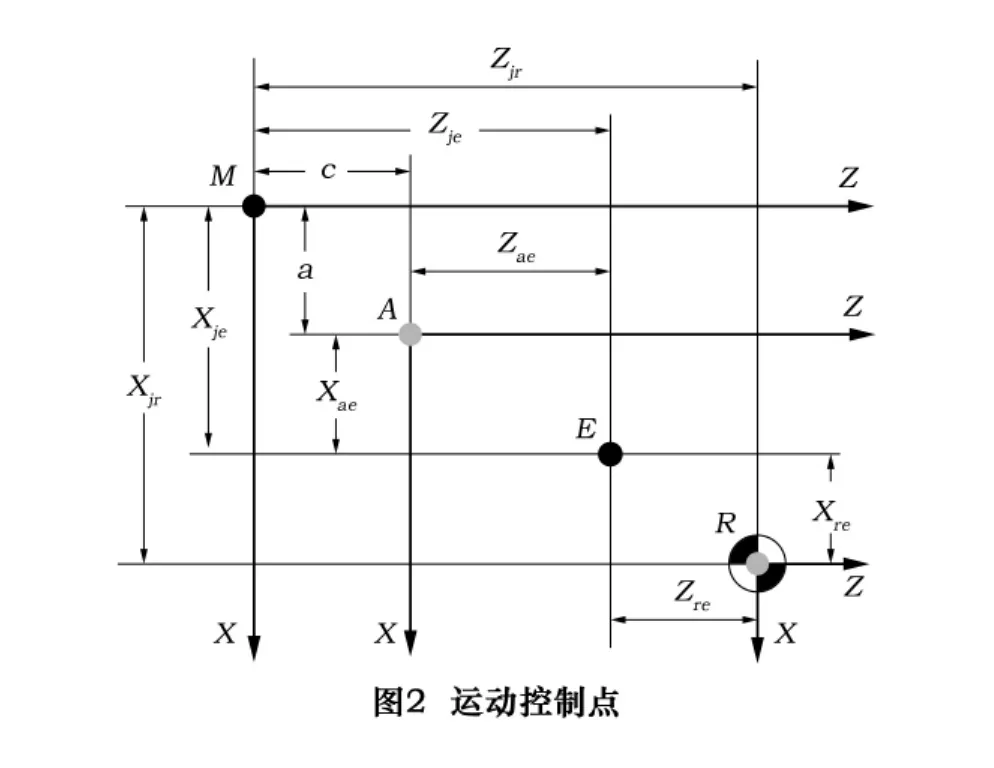
刀具参考点是机床在返回到R点时刀架内或刀架延伸部分内与R重合的那一点，也叫E点，E点在刀架上是固定的，在机床内是运动的。E点的相对坐标记为（Xre，Zre），如图2。相对坐标系用来记录刀架移动后相对位置编码器的输出值（刀架移动量），可见数控系统在机床坐标系中的运动控制是在相对坐标系建立后确立的。

在R点位置，数控系统将相对坐标清零，运动控制点即是刀架上的E点。由图2可知，任意时刻E点的机床坐标与相对坐标的关系，为式（2）所示。CRT上显示的正是E点的机床坐标和相对坐标。

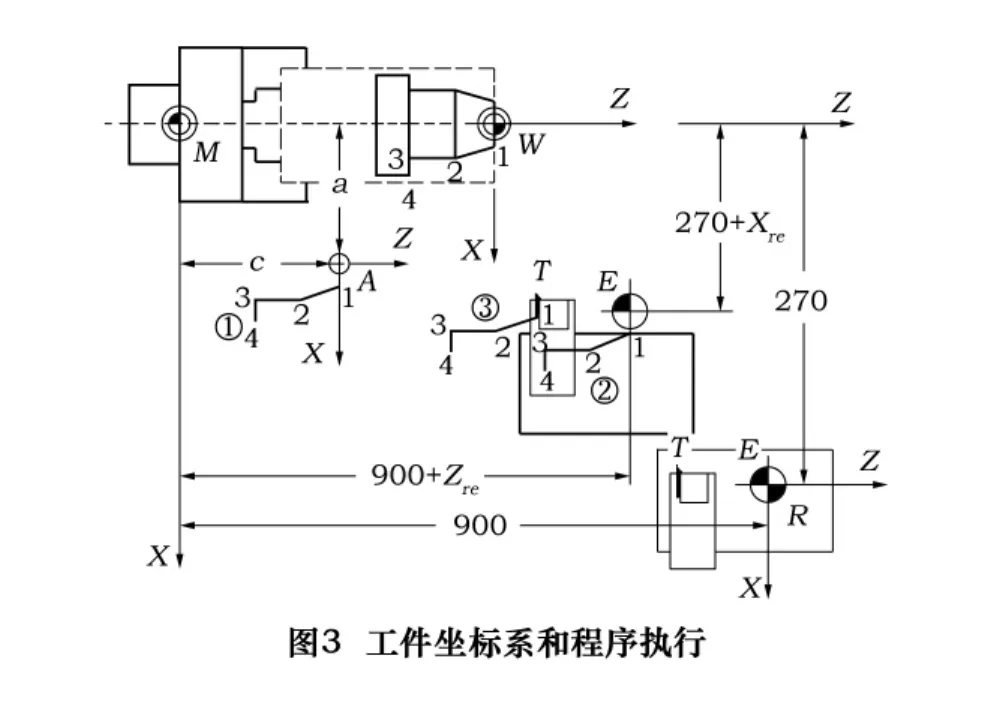
在刀具安装后，刀具T点相对于E点的位置关系是固定不变的，因此T的运动轨迹和E点的运动轨迹是完全相似的，如图3的②和③。因此数控系统控制E点后就间接或相对地控制了T点（刀具）。

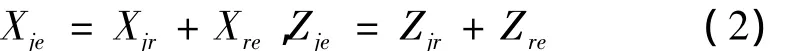
1．3 绝对坐标系

绝对坐标系是数控系统在R点时内建的另一个浮动的坐标参照系统，其原点称为绝对原点，也叫A点。A点的机床坐标（a，c）预置在CNC系统内，在R点建立机床坐标系后，CNC调用A点的机床坐标（a，c）建立绝对坐标系，如图2的AXZ。该坐标系中的坐标以“绝对坐标”的形式在CRT上显示。绝对坐标系具有以下属性:

（1）绝对坐标系被数控系统作为用户程序的执行坐标系，即数控系统把用户程序中的坐标视为绝对坐标，所以绝对坐标也称为执行坐标。

（2）A点的机床坐标（a，c）在数控系统内部为变量，用户可以给a和c赋予不同的值，从而改变A点的位置。也就是说用户可以通过面板操作或G代码来改变机床坐标（a，c），从而移动绝对坐标系。

由图2和公式（2）可求出任意时刻E点的绝对坐标（执行坐标）的表达式，公式（3），E点成为用户程序的执行点。

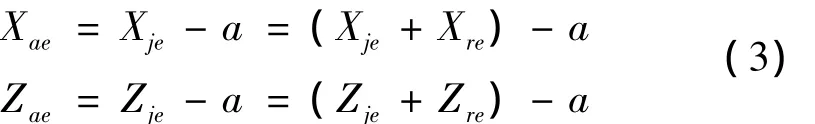
2 编程坐标系和工件坐标系

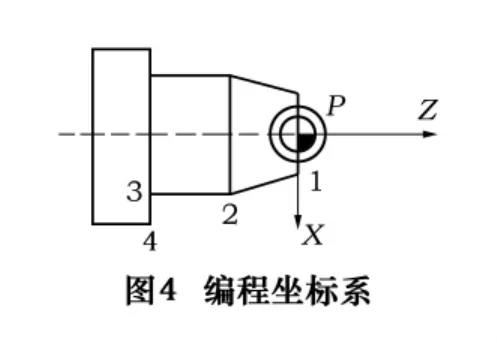
当编制图4所示工件的加工程序时，必须在工件图纸上设置一个坐标系。这个在工件图纸上设置的坐标系称为编程坐标系，其坐标原点称为编程原点，也称为P点。

例如在工件的右端面中心设置一个编程坐标系，编制了一个从P→1→2→3→4的用户程序，即假定了T点从P点出发，经过1点、2点和3点最终到达4点。用户程序的编制是基于编程坐标系PXZ的，它与机床（机床坐标系、工件和刀具的装夹位置）是无关的。

当工件和刀具在机床上装夹以后，要运行用户程序P→1→2→3→4，必须在工件上相应于编程坐标系的位置建立另一个用户坐标系，这个坐标系称为工件坐标系WXZ，其原点称为工件原点，也叫W点，如图3。显然对用户而言，工件坐标系WXZ是用户程序的执行坐标系，而T点是用户程序的执行点。

用户程序的运行是基于工件坐标系WXZ的，它与机床（机床坐标系、工件和刀具的装夹位置）是有关的。如果数控系统知道W点的机床坐标，那么用户程序指定的坐标可换算成机床坐标，用户程序就可在机床坐标系中执行。现在W点的机床坐标无法测量，那么用户程序怎样才能正确执行呢?

3 对刀和对刀原理

3．1 对刀原理和对刀

如上所述，对用户而言，工件坐标系WXZ是用户程序的执行坐标系，T点是用户程序的执行点，对数控系统而言，绝对坐标系AXZ是用户程序的执行坐标系，E点是用户程序的执行点。数控系统执行用户程序是把用户程序指定的坐标视为绝对坐标（Xae，Zae），并按公式（3）解出（Xre，Zre），然后控制E点运动。由于绝对坐标系AXZ并不在希望的位置，E点执行用户程序的结果并不是用户所希望的结果，如图3的①。

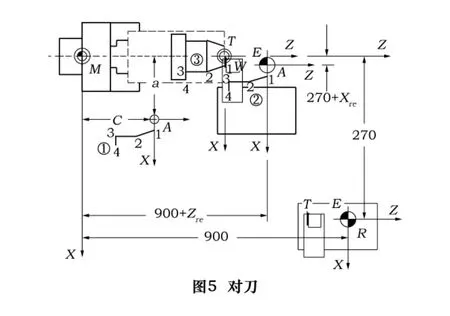
由于T点相对于E点有固定不变的位置关系，T点的运动轨迹和E点的运动轨迹完全相似，如图3的②和③。如果能使绝对坐标系AXZ相对于工件坐标系WXZ的位置关系相同于E点相对于T点的位置关系，那么数控系统控制E点在AXZ中执行用户程序的结果会导致T点在WXZ中得到同样的结果，如图5的②和③，而这正是用户所希望的结果。

用户可以在机床坐标域中移动绝对坐标系到任意位置，所以这点是可以做到的。这正是数控系统内建绝对坐标系并把它作为用户程序执行坐标系的原因。

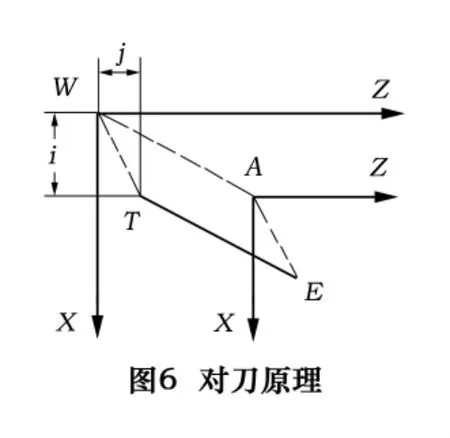
如图6所示，E点相对于T点有固定不变的位置关系，若使T点在工件坐标系WXZ中有工件坐标（i，j），于此同时使E点在绝对坐标系中有绝对坐标（i，j）。可以证明从此A点相对于W点的位置关系等同于E点相对于T点的位置关系，这就是对刀原理。

在工件坐标系中具有工件坐标（i，j）的点称为对刀点，对刀就是使T点与对刀点（间接或直接）重合。

在对刀位置，E点的相对坐标（Xre，Zre）有确定的值，根据对刀原理，令Xae=i，Zae=j，由公式（3）解出A点的新机床坐标（a，c），有:

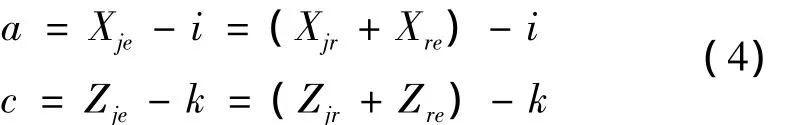
公式（4）是数控系统移动绝对坐标系的计算式。图5所示即是机床R点的坐标为（270，900），对刀点的工件坐标为（0，0）并由公式（4）移动绝对坐标系后的情况，E点在AXZ坐标系中的坐标为（0，0）。此时在AXZ中运行用户程序，则CNC控制E点在AXZ中走出轨迹②，同时T点会在WXZ中走出轨迹③，这正是用户希望的结果。