基于多周期GARCH-M模型的短期电价预测

王瑞庆，王弗雄,马杰,肖自乾

（海南软件职业技术学院软件工程系，海南琼海571400）

电价是电力市场供求平衡时形成的出清价，不仅受气象、系统负荷、发电成本、可用发电容量、输电网络阻塞等客观因素的影响，还受到市场交易规则、参与者的竞价策略及其对价格的心理反映等主观因素的影响，这些因素使得准确的电价预测较为困难。当前的预测方法主要包括通过模拟电力市场竞争规则来预测市场出清电价的长期预测方法和依据大量历史数据建立反映电价变化规律数学模型的短期预测方法[1]。

神经网络对非确定性、非精确性规律具有自适应能力，能够有效地处理多变量和非线性问题[2-5]。文献[2-3]分别使用粒子群优化和Levenberg-Marquardt训练方法的三层前馈神经网络对PJM和加利福尼亚电力市场的现货电价进行了预测。文献[4-5]指出高斯径向基函数神经网络比传统神经网络具有更快的学习速度和更好的逼近性能，更加适合于短期电价的预测。文献[6-10]分别提出了神经网络与模糊逻辑、Kalman滤波、支持向量机等相结合的短期电价预测方法，结果表明，混合预测方法比单独使用神经网络具有更好的预测效果。但由于神经网络方法的参数调整不够灵活，学习速度较慢，在实际应用中遇到了困难。

时间序列方法需要的历史数据相对较少，能准确地反映历史电价变化的连续性，比较常用的有自回归滑动平均模型（ARMA）和带外生解释变量的ARMA模型（ARMAX）。文献[11]建立了一个以负荷作为外生解释变量的ARMAX模型，结果表明，残差的实际分布与理论假设存在较大误差，在一定程度上影响了电价预测的精度。文献[12]注意到大多数电价序列均是非平稳随机过程的特点，提出了一种基于自回归积分滑动平均模型（ARIMA）的电价预测方法。文献[13]注意到不同时段也是一个影响电价变动的重要因素，建立了一个基于ARMA的分时段电价预测模型，使得对价格飞升（price spikes）的预测准确度得到了较大的提高。文献[14-15]分别建立了将误差校正、小波变换与ARIMA相结合的电价预测模型。文献[16]建立了一个考虑电价序列的非平稳、分时段和负荷因素的传递函数预测模型，进一步提高了电价预测的准确性。但这些模型均基于电价服从常方差正态分布的假设，不能有效地处理电价序列的异方差性，同时待估参数较多，难于大量应用。

本文在文献[11]的研究基础上，进一步分析了电力市场现货电价的影响因素和波动规律，提出了一种采用虚拟变量和正弦函数来刻画现货电价序列多周期性特征的GARCH-M模型。该模型易于定阶、待估参数少，可同时处理电价序列的趋势变化、多重周期、异方差及其与负荷之间的非线性相关性，具有一定的实用价值。对PJM电力市场历史数据的分析表明，电价分布的异方差和负荷的平方对电价的均值具有显著的影响，电价序列具有周、半月、月、季、半年等多重周期和明显的波动集聚效应，其残差的理论和实际拟合程度与文献[11]相比有较大程度的提高。

1 分析模型及求解方法

1.1 多周期GARCH-M模型

电价预测模型可以看作一个多输入单输出系统，输出为当期电价，输入为系统负荷、参与者的报价策略、燃料价格、季节、气候等影响因素。考虑到系统负荷和电价在各个电力市场中均是公开信息，因此，本文选择当期负荷、历史负荷与历史电价作为输入，并使用时间序列分析的GARCH-M模型对这一系统进行描述。设pt表示t期的现货电价，dt表示期残差表示的条件方差表示归一化残差，则描述电价变化的多周期GARCH-M模型可表述为

i

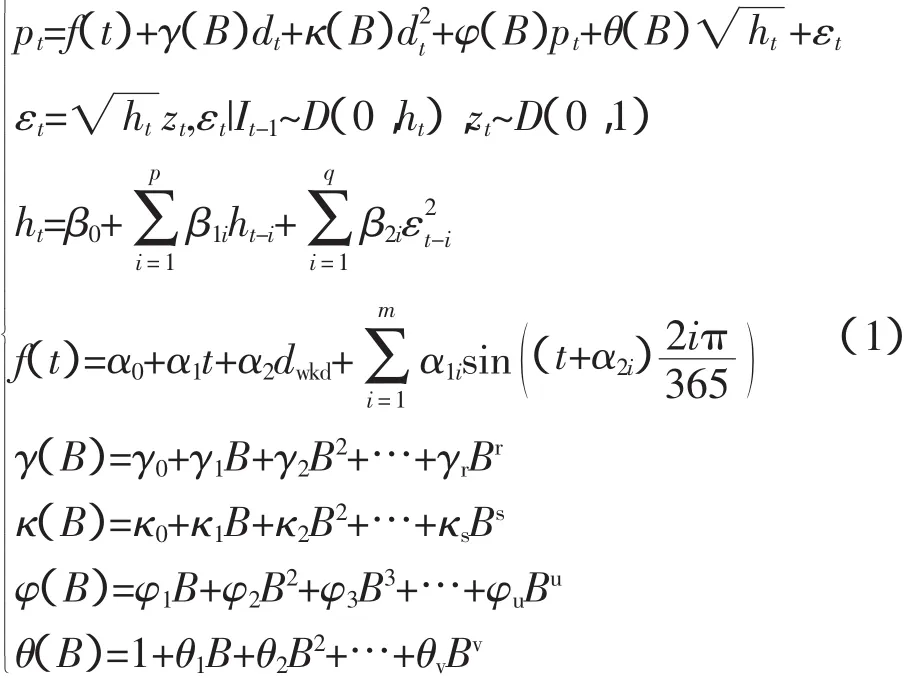
式中，B为滞后算子；m为电价一年内的变化周期数；u、v、r、s分别为均值方程中电价、条件方差的平方根、负荷及负荷平方的滞后阶数；p、q为条件方差方程中条件方差和残差平方的滞后阶数；It-1为t-1期的可用信息集；f（t）描述电价序列的趋势和季节性变化，dwkd是一个表示周周期的虚拟变量（工作日取值为1，休息日为0）。α=（α0，α1，α2，α3，α11，…，α1m，α21，…，α2m）、γ=（γ1，…，γr）、κ=（κ1，…，κs）、φ=（φ1，…，φu）、θ=（θ1，…，θv）、β=（β0，β11，…，β1p，β21，…，β2q）为待估参数。通过使用多个正弦函数可以允许电价序列存在多个周期，每个周期的幅度和峰值位置分别由α1i和α2i描述。为保证条件异方差为正，要求β0＞0，β1i，β2j≥0，坌i∈[1，p]，j∈[1，q]。

1.2 模型定阶

通过对去趋势和周期变化后的电价序列pt-f（t）的自相关函数和偏自相关函数的分析，可以确定u的初始取值，r和s的初始取值可以通过观察电价序列与负荷、负荷平方的趋势图加以确定，p和q的取值一般不会超过2，可通过分析残差εt的平方的自相关函数和偏自关函数加以确定。

时间序列的自相关性可以使用自相关系数进行描述。对于给定时间序列{yt}，k期自相关系数ρk为

式中，n表示样本容量；y軃表示样本数据的算术平均值。

在给定yt-1，…，yt-k+1条件下，yt与yt-k之间的条件相关关系称为偏自相关，可以使用偏自相关系数ρkk描述，其计算公式为

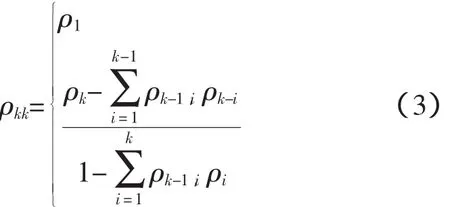
AR（p）序列的自相关函数随滞后期的增加，呈现指数或者正弦波衰减，逐渐趋近于0，而其偏自相关函数在k＞p后全都趋向于0。因此，可以根据偏自相关函数的截尾性来辨识AR（p）模型的参数p。

MA（q）序列的自相关函数在k＞q后全部趋向于0，而其偏自相关函数呈指数衰减，具有拖尾性。因此，可以根据自相关函数的截尾性来辨识MA（q）模型的参数q。

1.3 参数估计

若设白噪声序列zt的概率密度函数为正态分布，则εt的条件概率密度函数为[17]

若记ξ=（α，γ，κ，φ，θ，β，ht），则εt的样本对数似然函数可表示为

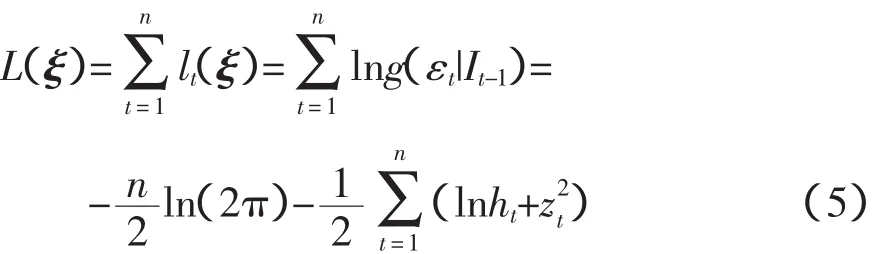
式中，n表示观察值的个数；lt（ξ）表示t期观察值的条件对数似然函数。通过最大化L（ξ），可以获得模型参数ξ的估计值ξ赞。

1.4 模型检验

大样本下，条件极大似然估计值ξ赞渐近服从式（6）表示的正态分布

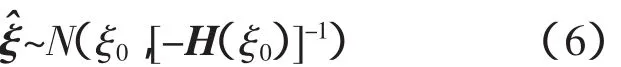
式中，ξ0为待估参数的真值；H为Hessian矩阵；可通过H（ξ0）≈坠L（ξ）/坠ξ坠ξ′｜ξ＝ξ赞估计。

残差的真实密度函数可能并不完全符合条件正态分布，因此有必要给出ξ赞的稳健方差，以便计算其渐近有效置信区间。ξ赞的稳健方差为矩阵Ω赞的对角元素。

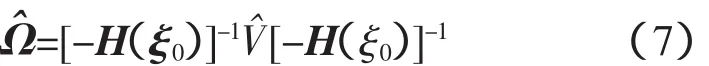
Nyblom统计量可用于检验模型的稳定性[17]，Nyblom统计量WN可表示为

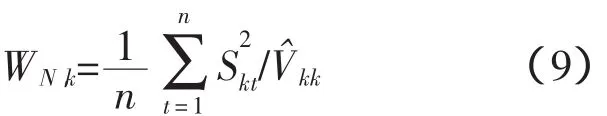
式中，Skt为St的第k个元素；V赞kk为V赞的第k个对角元素。

Cramer-Von Mises统计量可用于检验归一化残差zt是否符合条件正态分布。若正态分布的累积分布函数为FN（z），zt的实际累积分布函数为F（z），则Cramer-Von Mises统计量WCVM为

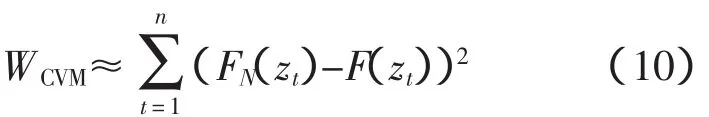
1.5 拟合精度评估

一般而言，电价序列预测模型是一个参数时变模型，其参数均需用最新的数据进行辩识，以便提高电价预测的准确性。本文采用平均绝对百分比误差（MAPE）来度量模型的预测精度，其表达式为

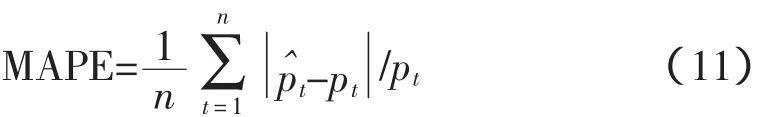
2 PJM电力市场实证

本文的研究样本来源于美国PJM电力市场2007年6月1日至2010年9月9日的日平均现货电价和负荷，样本总数为1197，日平均现货电价如图1所示。从图1可以看出，该电价序列存在明显的均值回复、尖峰跳跃、多重周期和异方差。

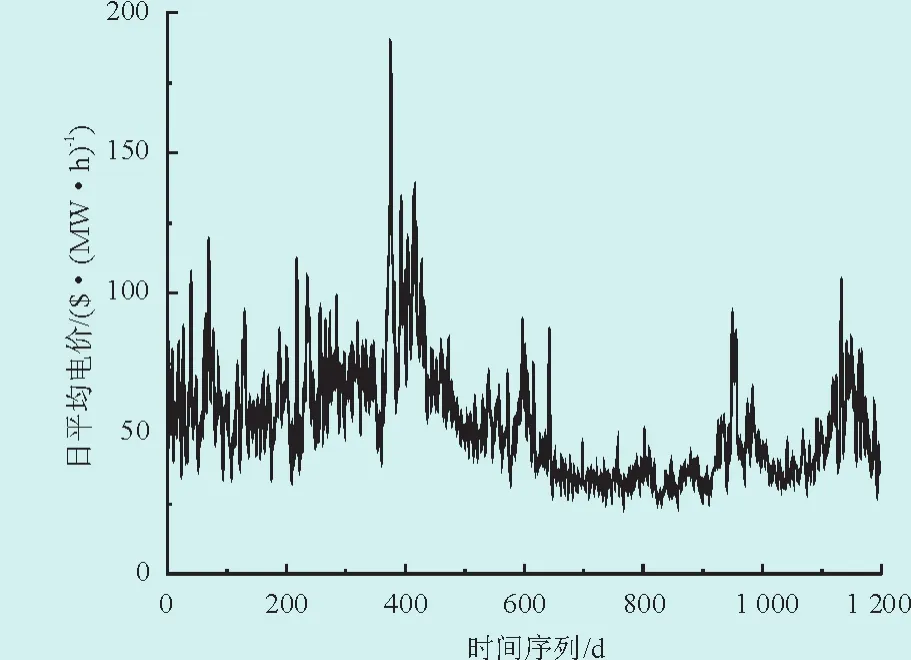
图1 PJM电力市场的日平均电价序列Fig.1 The time series of mean daily spot prices on PJM electricity market

表1给出了日平均现货电价和日平均负荷序列的描述性统计结果。从表1可看出，2个样本的偏度系数和峰度系数都显著异于正态，现货电价和负荷序列均呈现明显的右偏形态，同时具有较为明显的尖峰胖尾特征。J-B统计量非常显著，说明样本期间内现货电价和负荷的分布具有非正态性。

对样本数据的趋势图及相关系数进行分析，可将多周期GARCH-M模型具体化为（m，u，v，r，s，p，q），分别取值（24，4，1，1，1，1，1），并使用极大似然法对模型参数进行估计。表2给出了剔除在95%置信水平上不显著的参数后（截距项除外）的估计结果。

表1 样本数据的描述性统计结果Tab.1 Descriptive statistics of the sample data

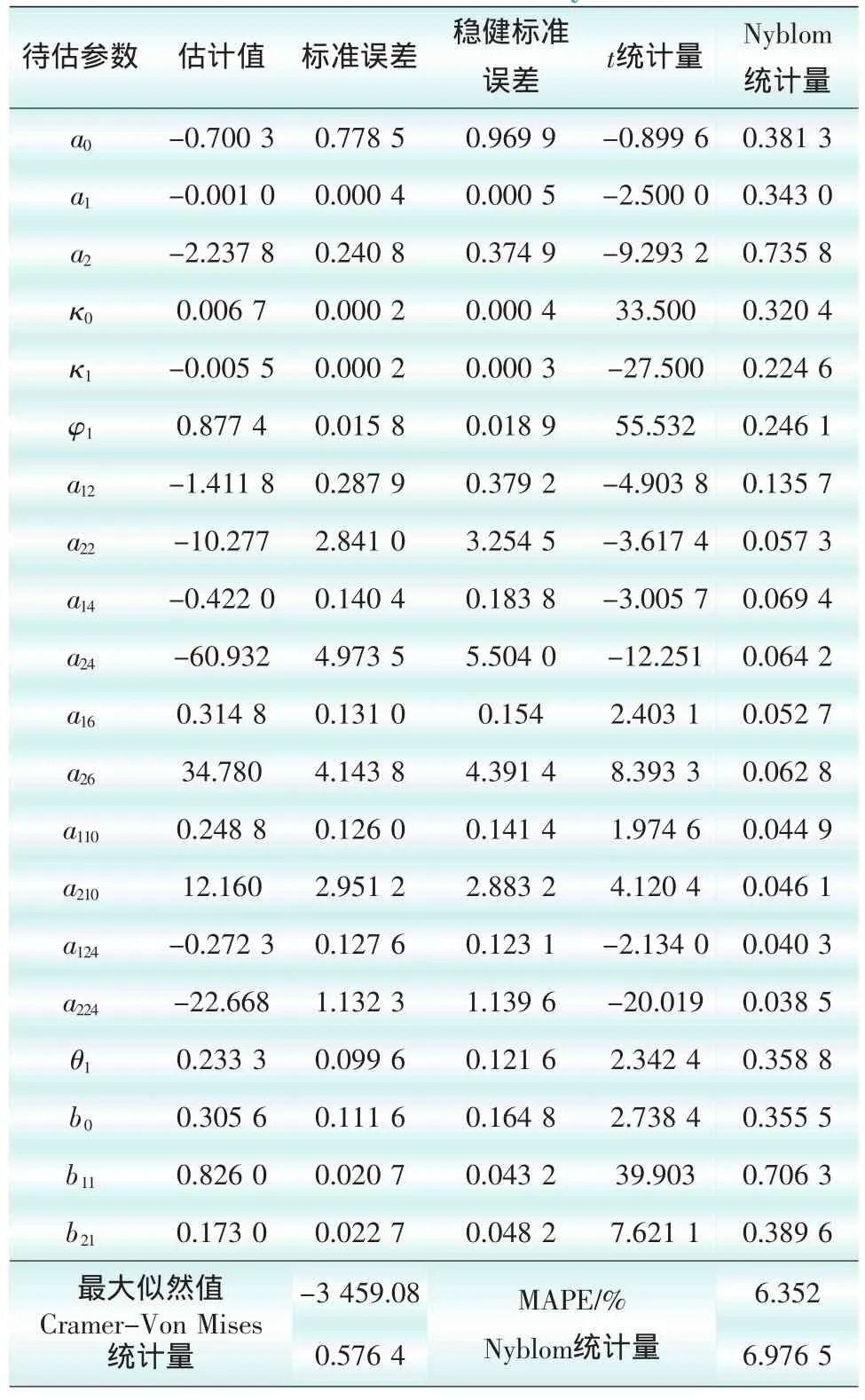
表2 多周期GARCH-M模型的估计结果Tab.2 Estimation results of multicycle GARCH-M

对表2的数据进行分析，可以得到如下结论：

1）模型的拟合精度（MAPE）6.352%与文献[12-16]相当，远少于文献[12-16]的待估参数个数，在一定程度上降低了模型的复杂度，提高了模型的计算速度及其实际应用能力。

2）参数a2和a1i、a2i、i I赞（2，4，6，10，24）的t统计量均在95%置信水平上，说明电价序列存在周、半月、月、季、半年等多周期效应，且周和半年周期的峰值幅度较大。

3）当在均值方程中包含负荷平方项时，各期负荷项的系数在95%置信水平上均不显著，表明现货电价与负荷平方之间的相关性要强于负荷，因此应通过在均值方程中包括负荷的平方项来描述电价与负荷之间的相关关系。

4）条件异方差对现货电价均值的影响显著（q1=0.233 3），在保持其它决定变量不变时，当电价波动性增强时，电价上升。

5）条件方差方程中b11=0.826，表明电价序列存在较强的波动集聚现象。而b11和b21之和为0.999，接近于1，说明电价序列可能存在共积GARCH效应。

6）Cramer-Von Mises统计量0.576 4略大于99%置信限临界值0.333，从图2可见残差序列存在明显的超额峰度，这表明多周期GARCH-M模型仍不能精确地描述电价序列的真实分布。

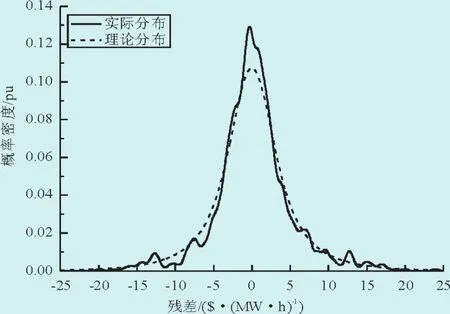
图2 残差的概率密度Fig.2 Probability density of the residuals

7）各待估参数的Nyblom统计量均小于其99%置信水平临界值0.748，但整个模型的Nyblom统计量（6.976 5）大于其99%置信水平下的临界值5.13，表明多周期GARCH-M模型存在一定程度的不稳定性，一个可能的原因是由于电价序列存在明显的右偏和尖峰厚尾，而这也是下一步要解决的主要问题。

3 结语

在文献[11]的研究基础上，进一步分析了电力市场现货电价的影响因素和波动规律，建立了一个采用虚拟变量和正弦函数来刻画现货电价序列多周期性特征的GARCH-M模型。该模型易于定阶、待估参数少，可同时处理电价序列的趋势变化、多重周期、异方差及其与负荷之间的非线性相关性，具有一定的实用价值。对PJM电力市场2007年6月1日至2010年9月9日的历史数据的算例分析表明，电价分布的异方差和负荷的平方对电价均值具有显著的影响，电价序列具有周、半月、月、季、半年等多重周期和明显的波动集聚效应。但本文模型关于残差符合正态分布的假设与残差的实际分布不能精确吻合，这在一定程度上降低了模型的拟合优度，因此如何进一步改进以提高模型的拟合优度是下一步要解决的问题。

[1] 陈思杰，周浩．电力市场电价预测方法综述[J]．继电器，2006，34（11）：54-60．CHENSi-jie,ZHOUHao.Electricity price forecast method of electricity market[J].Relay,2006,34（11）:54-60(in Chinese).

[2] 王立晶，刘丛．基于PSO训练BP神经网络的短期电价预测[J]．电力科学与工程，2008，24（10）：21-23．WANG Li-jing,LIU Cong.Short-term price forecasting based on PSO train BP neural network[J].Electric Power Scienceand Engineering,2008,24（10）:21-23(in Chinese).

[3] CATALAO J P S,MARIANO SJ P S,MENDES V M F,et al.Short-term electricity prices forecasting in a competitive market:a neural network approach[J].Electric Power System Research,2007,77（10）:1297-1304.

[4] GUO J J,PETER B L.Selecting input factors for clusters of Gaussian radial basis function networks to improve market clearing price prediction[J].IEEE Trans on Power Systems,2003,18（2）:665-672.

[5] 翁陈宇，陈维荣，罗小安．基于相似搜索和RBF神经网络的短期电价预测[J]．电力科学与工程，2007，23（1）：9-11．WENG Chen-yu,CHEN Wei-rong,LUO Xiao-an.Shortterm electricity price forecasting based on analogue search and RBF neural network[J].Electric Power Science and Engineering,2007,23（10）:9-11(in Chinese).

[6] HONG Y Y,HSIAO C Y.Locational marginal price forecastingin deregulated electricity marketsusingartificial intelli-gence[J].IEE Proc on Gener Transm.Distrib,2002,149（5）:621-626.

[7] CLAUDIA P R,GEORGE J A.Energy price forecasting in the Ontario competitive power system market[J].IEEE Trans on Power Systems,2004,19（1）:366-374.

[8] ZHANG Li,PETER B L.Neural network-based market clearing price prediction and confidence interval estimation with an improved extended kalman filter method[J].IEEE Trans on Power Systems,2005,20（1）:59-66.

[9] AMJADY N.Day-ahead price forecasting of electricity markets by a new fuzzy neural network[J].IEEE Trans on Power Systems,2006,21（2）:887-986.

[10]FAN S,MAO C,CHEN L.Next-day electricity price forecasting using a hybrid network[J].IEE Proc on Gener Transm Distrib,2007,1（1）:176-182.

[11]王瑞庆，季文天．基于有偏t分布ARMAX模型的短期电价预测[J].电网与清洁能源，2011，27（2）：19-23．WANG Rui-qing,JI Wen-tian.Short-term electricity price forecasting based on ARMAX model with skewed student-t distribution[J].Power System and Clean Energy,2011,27（2）:19-23(in Chinese).

[12]CONTRERAS J,ESPINOLA R,NOGALES F J,et al.ARIMA models to predict next-day electricity prices[J].IEEETrans on Power Systems,2003,18（3）:1014-1020.

[13]CUARESMA JC,HLOUSKOVA J,KOSSMEIER S,et al.Forecasting electricity spot-prices using linear univariate time-seriesmodels[J].Applied Energy,2004,77（1）:87-106.

[14]周明，严正，倪以信，等．含误差预测校正的ARIMA电价预测新方法[J]．中国电机工程学报，2004，24（12）：63-68．ZHOUMing,YANZheng,NIYi-xin,et al.A novel ARIMA approach on electricity price forecasting with the improvement of predicted error[J].Proceedings of the CSEE,2004,24（12）:63-68(in Chinese).

[15]CONEJOAJ,PLAZSAMA,ESPINOLAR,etal.Day-ahead electricity price forecasting using the wavelet transform and ARIMAmodels[J].IEEETranson Power Systems,2005,20（2）:1035-1042.

[16]陈友，王 ，李渝曾．一种用于短期电价预测的分时段时间序列传递函数模型[J]．电力系统保护与控制，2008，36（16）：1-4．CHEN You,WANG Xian,LI Yu-zeng.Electricity price forecasting based on transfer function models for perioddecoupled time series[J].Power System Protection and Control,2008,36（16）:1-4(in Chinese).

[17]NYBLOM J.Testing for the constancy of parameters over time[J].Journal of the American Statistical Association,1989,84（405）:223-230.