高海拔地区FDN型防振锤防晕性能优化

黄廷政，莫娟，彭宗仁，刘胜春，谢梁，雍丹萍

（1.中国电力科学研究院，北京100055；2.西安交通大学，陕西西安710049；3.国网电力科学研究院，湖北武汉430074；4.南京电力金具设计研究院，江苏 南京 210037）

输电线路上的导线由于受到各种因素的影响，会产生不同形式的振动。目前，已知在架空导线上发生振动的类型主要包括微风振动、次档距振荡、脱冰跳跃、电晕舞动等。其中，微风振动发生的地区最为普遍，也是危及导线安全运行最为严重的一种振动形式。

微风振动的特征是振幅小、频率高和持续时间长。振幅一般小于导线的直径，最大为导线直径的2~3倍，而振动频率一般在10~50 Hz，持续时间一般为数小时，在开阔地带和风速均匀稳定的情况下振动时间则更长。一年之中，微风振动的时间占全年时间的30%~50%。长时间的微风振动会使导线在悬挂点反复拗折，引起材料疲劳甚至断股、断裂或使金具、绝缘子损伤[1-2]。

为了降低导线随微风的振动强度，减缓导线受到的振动伤害，目前较为广泛采用的措施是在导线上安装防振锤。当导线发生振动时，防振锤随之上下运动，从而使钢绞线股之间产生摩擦，消耗导线传来的大部分能量。防振锤对减弱或消除导线振动危险的效果显著，可将导线的最大振幅降低至几分之一甚至几十分之一[3-4]。

我国常用的防振锤主要为Stockbridge型。按照锤头形状可分为FDN哑铃型、FR音叉型和FH环式扭矩型等。其中，FDN防振锤的锤头类似于两端为圆球的哑铃，两端的圆球直径不一，小球头直径较小，导致其场强较高，在高海拔地区运行时经常会发生电晕放电，对周围电磁环境造成污染[5-6]。

本文以330 kV输电线路用FDN型防振锤为研究对象，运用三维有限元方法计算其电场分布，并对其锤头结构进行优化，以降低其表面场强。根据优化方案制造试品，并对其进行不同气压下的电晕试验和功率特性试验，以保证其防晕和防振性能满足在高海拔地区运行的要求。

1 研究方法

国内外对于金具的表面和附近电压及电场分布的计算研究所采用的数值计算方法有两大类：微分法和积分法。微分法主要包括差分法和有限元法，积分法包括模拟电荷法和边界元法。由于每种方法各有利弊，所以近年来又出现了多种方法的耦合结合使用，比如有限元与边界元法、有限元与模拟电荷法、有限元与积分方程法等，实现不同方法的优势互补，以期解决多子域、多连通域的复杂问题。

有限元法是以变分原理为基础，吸取差分思想而发展起来的一种数值计算方法。静电场的能量可表示为待定的电位函数及其导数的积分式，对于求解场域，依照差分法的离散化方法，将它划分为有限个子区域（称为单元）。然后利用这些离散的单元，使静电场能量近似地表示为有限个节点电位的函数。这样，求静电场能量极值的变分问题就简化为多元函数的极值问题，而后者通常归结为一组多元线性代数方程——有限元方程。最后结合方程组的具体特征，利用适当的代数方法，求得各节点电位，实现变分问题的离散解[7-8]。

本文运用三维有限元仿真软件ANSYS建立FDN型防振锤的计算模型，计算其表面电场分布，分析可能发生电晕的部位，据此提出了结构优化方案[9]。

2 计算模型

FDN型防振锤的原结构实物如图1所示，该防振锤主要由锤头、钢绞线和固定线夹组成。线夹位于钢绞线中部位置，两侧为不对称结构，各有锤头一个，锤头形状相同，小球头的朝向相反。

根据330 kV输电线路耐张塔、导线、防振锤的实际尺寸建立三维有限元模型，杆塔呼称高18.5 m，采用分裂间距为400 mm的双导线，防振锤计算模型如图2所示。

330 kV线路最高运行线电压为345 kV，因此计算时导线和防振锤上施加最高运行相电压的峰值

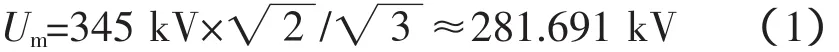
3 计算结果

经仿真计算，得到FDN型防振锤表面的电场分布如图3所示。该图为锤头剖面视图，其中，不同的颜色对应不同的电场强度，红色的为高电场，深蓝色的为低电场。由图中可见，锤头的两端场强相对较高，尤其是小锤头，底端弧面最高场强为2 987 V/mm，大锤头则直径较大，且受到导线屏蔽，场强较低。

图1 FDN型防振锤典型实物图Fig.1 Typical object of the FDN-typed damper

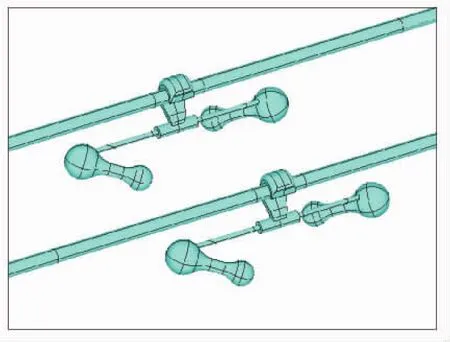
图2 FDN型防振锤三维有限元模型Fig.2 Three-dimensional finite element model of the FDN-typed damper

由PEEK公式可知，在极不均匀电场下，金具表面空气的局部放电临界场强峰值在3 000 V/mm左右[11]。在高海拔地区，由于气压较低，电极布置形式相同时，其起晕电压会随之下降，起晕场强也会相应降低[12]。因此，FDN型防振锤的小锤头在海拔较高的线路上应用时容易发生电晕放电，因而应对锤头结构进行优化设计，减小锤头表面的最大场强值。

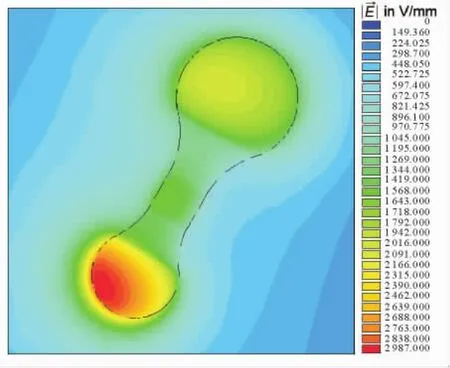
图3 FDN型防振锤电场分布Fig.3 Electric field distribution of the FDN-typed damper

经过一系列仿真计算和方案调整，在考虑技术经济性的前提下，最终确定了较为合适的结构优化方案，将小锤头的半径由25 mm增大至35 mm，同时优化大小锤头之间的连接曲率半径，确保整个锤头表面的光滑连接。此时，最大场强仍然出现在小锤头外侧表面，但其表面场强大大降低，仅为2 390 V/mm，防晕性能显著提高。

4 试验验证

根据上述优化结果，制造了相应的试品，如图4所示。为了验证其电气和力学性能，需要进行不同海拔下的电晕试验和功率特性测试。

图4 优化后FDN型防振锤实物图Fig.4 Real object of the FDN-typed damper optimized

4.1 不同气压下的电晕试验

为了模拟高海拔下的环境条件，电晕试验在特高压交流试验基地的环境气候室中进行，该气候室可利用真空系统模拟不同海拔下的低气压。试品布置如图5所示，试品悬挂于双分裂模拟导线中部，距地面4 m。试验地点海拔高度为19 m，采用紫外成像仪观察试品的电晕放电。依据GB/T 2317.2-2008，在海拔1 000 m及以下地区进行电晕试验时，试验电压Ut需满足下式[13]：

图5 优化后FDN型防振锤试验布置试Fig.5 Test arrangement of the FDN-typed damper optimized

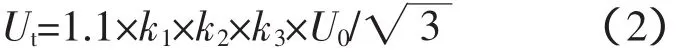
式中，U0表示系统最高运行线电压，kV；k1表示试品位置修正系数，塔窗附近金具取1.05；k2表示试品悬挂高度修正系数，330 kV金具悬挂高度为4 m时取1.0；k3表示气象修正系数，包括温度、湿度、气压等，根据本次试验条件，此处可取1。

将U0=345 kV，k1=1.05代入式（2）可得Ut=230 kV，即各海拔下起晕电压需高于此值。不同海拔下防振锤的起晕电压如表1所示，锤头在常压下的起晕电压为340 kV，海拔升至4 300 m时，防振锤的起晕电压降至234 kV，但依然高于230 kV。由此可见，优化后的FDN可满足4 300 m海拔下的防晕要求。

表1 优化后FDN型防振锤不同海拔下的起晕电压Tab.1 Corona inception voltages of the FDN-typed damper optimized under various altitudes

4.2 功率特性试验

功率特性是衡量防振锤性能的主要指标，表征了其消耗振动功率的能力。防振锤的功率特性受锤头质量、转动惯量和钢绞线长度等多方面因素的影响。由于导线系统振动的非线性和相关材料性能的分散性，难以通过理论计算分析防振锤的实际振动特性，必须采用模拟试验进行测量，才能获得较为真实的结果。

防振锤的功率特性试验依据标准DL/T 1099-2009进行，试验时防振锤被固定于电动振动台上，施以正弦激振力，在恒速条件下测定其谐振频率及功率特性[14-15]。

FDN每个锤头的振动包括上下摆动和自身回转2种形式，而两侧的锤头由于非对称布置，因而共可产生4个谐振频率，防振锤在此频率附近振动时所消耗的能量最大。优化前后FDN的功率特性曲线如图6所示，优化前的4个谐振频率在5.0~95.0 Hz，分布过于分散，大大高于其适配导线的微风振动的频率范围，并且功率相差较大，最大峰值达2.71 W，而最小峰值仅为0.58 W，峰谷值之比也大于5，不满足标准要求；优化后谐振频率在5.0~55.0 Hz，4个峰值差别较小，最大为1.83 W，最小为1.31 W，谐振频率和功率分布更为合理，功率峰谷值之比也小于5，各项指标显著优于前者，完全满足标准要求。

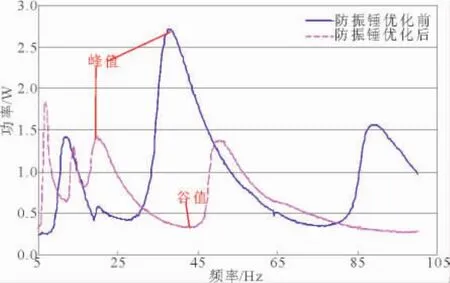
图6 优化前、后FDN型防振锤功率特性曲线Fig.6 Power characteristic curves of the FDN-typed damper before and after optimization

由此可见，结构优化后的FDN功率特性更为合理和优良，具有良好的防振效果，可以在高海拔地区进行推广应用。

5 结论

通过对330 kV线路用防振锤FDN进行电场分析、结构优化、试品制造、电晕试验和功率特性试验，可得出以下结论。

1）原结构的FDN防振锤哑铃形锤头下端球头半径较小，不适合应用在高海拔地区。计算结果表明，原结构的小锤头外侧表面场强较高，最高达2 987 V/mm，进行结构优化后，其表面场强降至2 390 V/mm以下。

2）优化后的FDN型防振锤防晕性能良好，可应用于海拔4 300 m以下的330 kV输电线路。此外，新结构防振锤的功率特性较旧结构更好，峰谷比更低，防振性能更优良。

[1] 梅丽佳．架空线路导线振动的危害及防振[J]．江西电力，2005，29（6）：30-34．MEI Li-jia．Vibration hazards and anti-vibration of overhead line conductors[J]．Jiangxi Electric Power，2005，29（6）：30-34(in Chinese)．

[2] 王藏柱，杨晓红．输电线路导线的振动和防振[J]．电力情报，2002（1）：69-70．WANG Cang-zhu，YANG Xiao-hong．Vibration of electric power lines and its countermeasures[J]．Information on Electric Power，2002（1）：69-70(in Chinese)．

[3] 李瑞，余虹云，刘新，等．防振锤的优化设计[J]．中国电力，1997，30(5)：60-61．LI Rui，YU Hong-yun，LIU Xin，et al．Optimal design of vibration damper[J]．Electric Power，1997，30(5)：60-61(in Chinese)．

[4] 徐乃管，王景朝，董玉明．关于防振锤力学性能的探讨[J]．电力建设，2001，22(3)：8-11．XU Nai-guan，WANGJing-chao，DONG Yu-ming．Inquire into mechanical properties of vibrating dampers[J]．Electric Power Construction，2001，22(3)：8-11(in Chinese)．

[5] 谢天喜，莫娟，彭宗仁，等．500 kV紧凑型线路悬垂复合绝缘子均压环电晕抑制分析[J]．高电压技术，2010，36(7)：1779-1784．XIE Tian-xi，MO Juan，PENG Zong-ren，et al．Corona suppression of grading rings on suspension composite insulators on 500 kV compact transmission line[J]．High Voltage Engineering，2010，36(7)：1779-1784(in Chinese)．

[6] 邬雄，聂定珍，万保权，等．架空送电线路的电磁环境及其污染影响[J]．高电压技术，2000，26(5)：24-26，77．WUXiong，NIEDing-zhen，WANBao-quan，et al．Electromagnetic environment of the overhead transmission lines and electromagnetic pollution[J]．High Voltage Engineering，2000，26(5)：24-26，77(in Chinese)．

[7] 王 成．有限单元法[M]．北京：清华大学出版社，2003：13-36．

[8] 龚曙光．ANSYS基础应用及范例解析[M]．北京：机械工业出版社，2003：351-364．

[9] 谢天喜，刘鹏，李靖，等．交流1 000 kV同塔双回输电线路复合绝缘子电场分布[J]．高电压技术，2010，36(1)：224-229．XIETian-xi，LIUPeng，LIJing，et al．Electric field distribution of composite insulator on AC 1 000 kV double circuit transmission line on the same tower[J]．High Voltage Engineering，2010，36(1)：224-229(in Chinese)．

[10]XIE Tian-xi，PENG Zong-ren．Study on the voltagesharing performance of porcelain insulators on 750 kV compact double circuit transmission line[C]//Proceedings of the 9th International Conference on Properties and Applications of Dielectric Materials．Harbin，China：IEEE，2009：192-195．

[11]PEEK F W．Dielectric phenomena in high voltage engineering[M]．New York：Mc-Graw-Hill，1929：38-50．

[12]刘其 ．电气绝缘结构设计原理:中册[M]．北京：机械工业出版社，2003：71-78．

[13]GB/T 2317．2-2008 电力金具试验方法（第2部分）：电晕和无线电干扰试验[S]．北京：中国标准出版社，2008．

[14]周立宪，王景朝，侯继勇，等．防振锤技术参数对其功率特性的影响分析[J]．电力建设，2008，29(5)：26-29．ZHOU Li-xian，WANG Jing-chao，HOU Ji-yong，et al．Influence of the technical parameters of vibration dampers on their power characteristics[J]．Electric Power Construction，2008，29(5)：26-29(in Chinese)．

[15]徐乃管，王景朝，董玉明．关于防振锤力学性能的探讨[J]．电力建设，2001，22(3)：8-11．XU Nai-guan，WANG Jing-chao，DONG Yu-ming．Inquire into mechanical properties of vibrating dampers[J]．Electric Power Construction，2001，22(3)：8-11(in Chinese)．