振动频谱法在架空输电线路张力检测中的应用

周海滨，董明，任重，余建国，王国利

（1.西安交通大学电力设备电气绝缘国家重点实验室，陕西西安710049；2.特高压工程技术（昆明、广州）国家工程实验室，广东广州510623）

架空输电线路处于户外，运行环境恶劣，经常受到风雨雪等外力影响，导线上张力随负载不同而变化。准确、无损、便捷、实时地获得导线张力，对预防架空输电线路断线、倒塔事故，保证电力系统输电工程安全稳定运行具有重要意义[1-2]。

电力系统架空输电线路杆塔拉线张力测量问题与斜拉桥缆索张力测量问题相似，均不适合截断缆索对张力进行直接测量。一般认为，索力测试的方法分为5种：1）压力表读数法；2）压力传感器法；3）振动频率法；4）电磁测量法；5）静力方法[3-4]。压力表读数法一般适用于工程施工过程当中，不宜用于长期张力检测。压力传感器法可以实现拉力长期监测，但必须在施工过程中进行安装，对已有工程改造难度大，且价格昂贵。振动频率法安装方便，是目前应用较广泛张力测量方法，但其存在如下缺点：1）测量的精度受到缆索抗弯刚度、垂度、斜度、边界条件和环境因素等诸多因素的影响，误差较大；2）只适用于测量长径比较大的细长索体，即通常所说的“弦长索体”，对于长径比较小的短索，测试的误差就会显著增大。电磁测量法根据导磁材料的磁性参数变化，推算出索力大小。静力方法是根据力的分解和平衡原理，采用三点弯曲法求得索力大小，该方法适用于直径小于44 mm的细索，测试原理简单，效果较好[5]。本文采用振动频率法对架空输电线路张力进行间接测量，导线张力的基准标定方案选取基于静力分解原理的旁压式张力传感器。

本文基于架空输电线路微风振动机理，给出了小垂跨比条件下导线张力与振动本征频率之间的关系理论模型，从理论上证实了导线张力与本征频率之间存在着对应关系。研发了基于振动频谱机理的架空输电线路张力检测系统，并利用该系统对实验线路进行了实测，验证了理论模型及测试系统的有效性。

1 微风振动理论分析

架空输电线路一般跨度较大，暴露于户外，工作过程中受到风载荷、雨雪载荷等的作用，会发生振动现象。根据引起导线振动的原因和导线振动的形式不同，可以将导线振动分为微风振动、次档距振荡、舞动、脱冰跳跃、横向碰击和湍流振动等形式[6]。

线路微风振动是指在风速不大的情况下产生的垂直平面内的低幅值高频率的周期振动现象[7]，起振条件要求风速在0.5～10.0 m/s。风速过小，能量不够，不足以推动导线上下振动；风速过大，气流与地面磨擦加剧，使地面以上一定高度风速均匀性遭到破坏，令导线处在紊流风速中，而不能形成稳定振动。风向与线路走向成45°~90°时易发生微风振动，20°以下一般不发生振动，导线悬挂越高，越容易起振。微风振动产生条件容易满足，一般认为线路一直处于微风振动状态[8]。

微风振动通常采用卡尔曼（Karman）漩涡和“锁定效应”现象进行解释。当架空输电线路受到稳定的横向均匀风力或具有横向分量的风力作用时，在导线背风面产生的上下交替的气流漩涡，称为卡尔曼漩涡[7]，如图1所示[9]。

卡尔曼漩涡脱落频率fs与导线直径D以及吹过导线风速Vs有关，关系式如下[10]：

式中，S为司脱罗哈系数。

图1 稳定侧风下圆柱体背侧漩涡脱落现象Fig.1 Vortex shedding from a stationary circular cylinder in a uniform crosswind

漩涡脱落频率即为线路微风振动激发频率，线路导线直径、风速均与振动频率密切相关[11]。当漩涡脱落频率与导线本征频率接近时，该频率下振幅得到放大，即为线路微风振动的主要表现，风速在一定范围内变化时，漩涡脱落频率不变，仍保持在本征频率附近，该现象成为“锁定效应”[8]。

Irvine对可伸长、弹性、小垂跨比（<1：8）等高悬索进行了研究，指出可将其振动分解为3种情况，即与线路走向垂直的水平横向振动、悬索面内垂直振动和面内水平方向振动，其中面内水平方向振动不易发生，可忽略[12]。对于架空线路，受到风的激励时，会同时产生水平横向振动和面内垂直振动。

2 振动频谱与张力关系模型

架空输电线路一般采用多股绞合的钢芯铝绞线，股与股之间存在着相对滑移，故其抗弯刚度EI变化很大，一般在16 N·m2~577 N·m2取值[13]。架空线路跨度较大，可达数百米，设架空输电线路满足无阻尼条件，利用弦振动模型模拟输电线误差很小[13-14]，其振动方程[15-16]如式（2）所示。

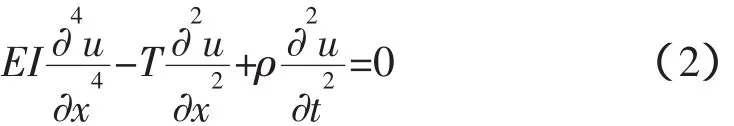
式中，x为导线水平方向坐标；u（x，t）为导线上各时刻横向位移；EI为导线抗弯刚度；T为绳索张力；ρ为绳索线密度。

对式（2）求解，可得张力计算方法如式（3）。

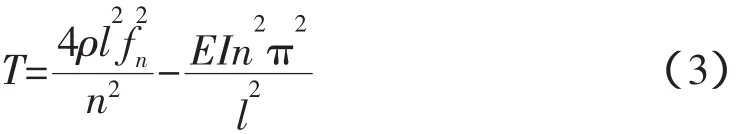
式中，n为导线自振频率的阶数，取值为正整数；fn为导线第n阶自振频率；l为架空导线相邻杆塔间隔距离。

架空输电线路跨度很大、垂跨比较小，此时可忽略导线弯曲刚度的影响，上式可简化为式（4）。

令n1和n2分别为两不同本征频率阶次为其对应振动频率，一般可采用式（5）对线路张力进行计算，以减小误差。

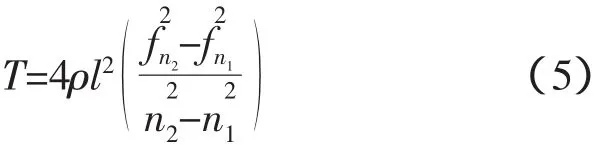
3 导线振动检测系统设计

为了实现对架空输电线路振动信号的实时在线测量，本文研发了基于嵌入式Linux系统的架空输电线路振动信息无线采集分析系统。该系统由振动检测无线传输系统、无线数据采集系统和上位机数据分析系统3个模块构成，能够实现振动信号测量、数据采集、无线信息传输、数据存储、状态展示和故障分析等功能，系统结构如图2所示。

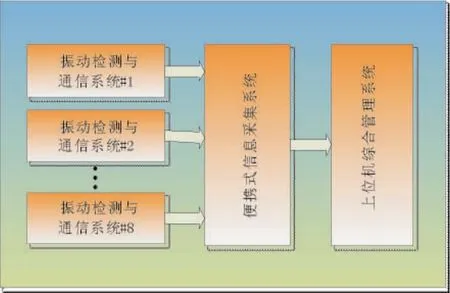
图2 系统硬件结构图Fig.2 Systemic hardware structure chart

3.1 振动检测与传输系统

该部分由电源模块、加速度传感器模块、2.4 GHz无线传输模块和控制器模块构成，其结构如图3所示。

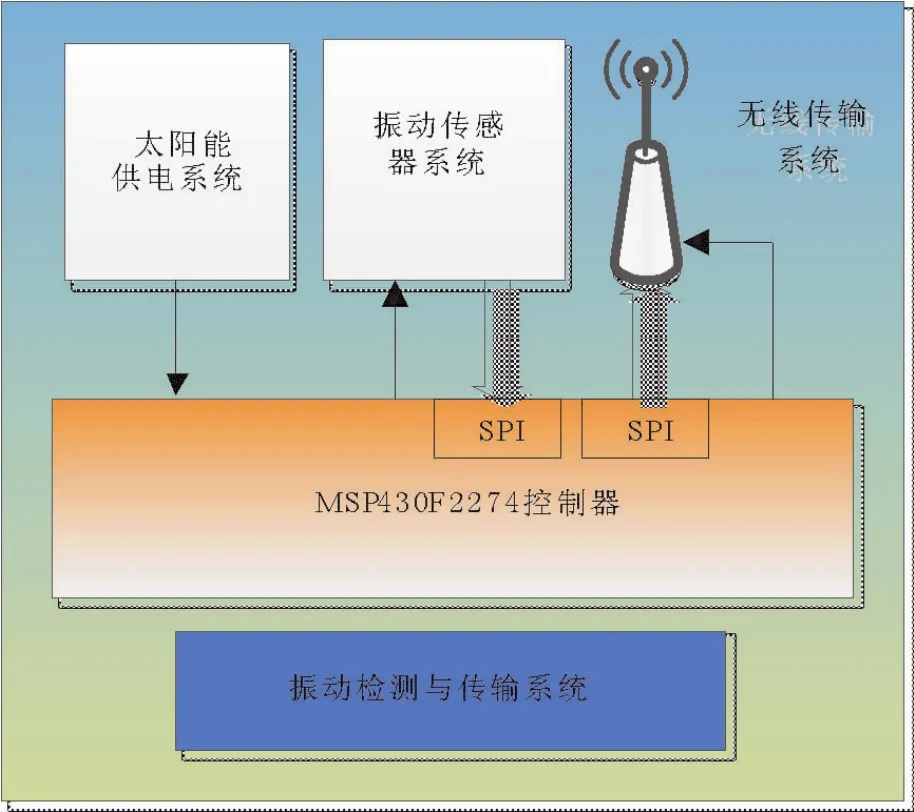
图3 振动检测与传输系统结构图Fig.3 Systemic structure chart of vibration detection and transmission

振动传感器数据采样率最高可达到3 200点/s，远大于微风振动的频率上限，能够同时测量与线路走向垂直的线路横向水平振动和竖向振动信号。考虑到本模块安装方式为附着于架空输电线路，需要对传感器模块的体积和重量进行优化设计，便于安装，同时减小安装传感器接入给原系统带来的影响。本文采用集成电路为主的元器件实现了传感器模块设计，将其体积控制在（1×2×2）cm3以内，质量控制在100 g以内，基本可忽略其对导线造成的影响，传感器外观如图4所示。

图4 传感器模块外观Fig.4 Outward appearance of vibration sensor

为了保证振动传感器测量稳定性，同时降低系统功耗，本文设计了“交替式”数据采集方案，在振动传感器模块存储空间开辟“A”和“B”2个缓冲区，交替使用以实现不间断的振动信息采集和定时的无线数据传输功能，实现逻辑如图5所示。

3.2 无线数据采集系统

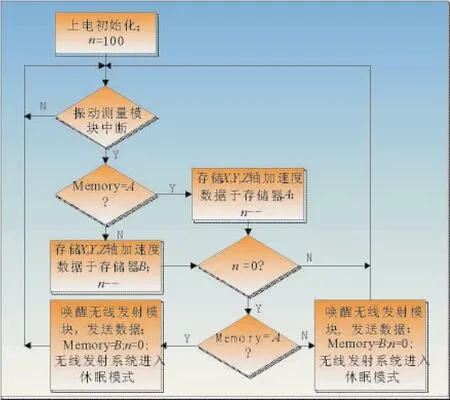
图5 “交替式”信息采集方案原理图Fig.5 Alternating data acquisition diagram

便携式无线信息采集系统是数据采集的中转环节，采用无线方式采集线路振动信息，并将其存储到嵌入式数据库中，并且依靠自身的LCD显示功能提供数据的实时展示功能。该部分采用嵌入式Linux系统实现，方便实现数据分析的高级功能，同时为接入网络预留了接口，便于升级。图6给出了该系统的结构示意图。

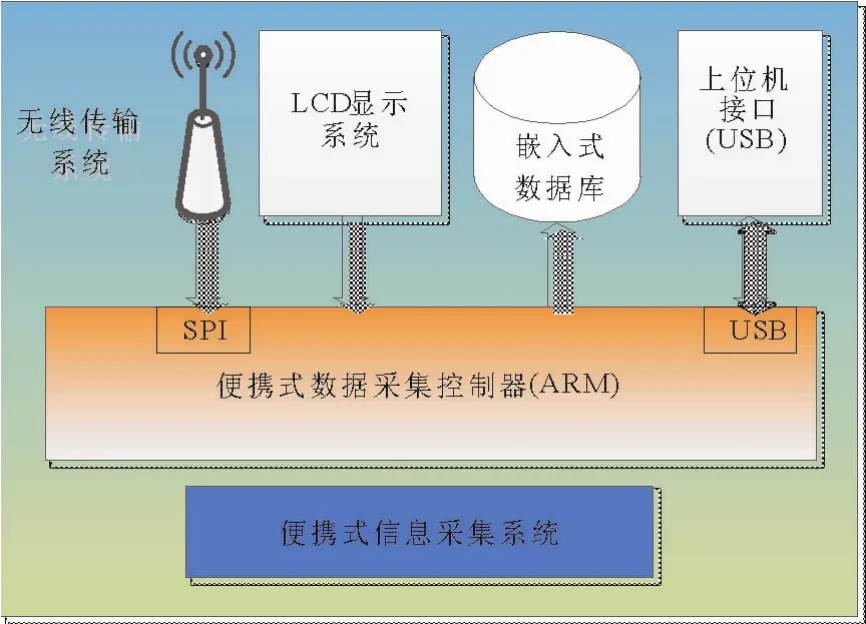
图6 便携式信息采集系统结构Fig.6 Structure chart of portable data acquisition system

3.3 上位机综合分析系统

上位机分析平台由软件编程实现，分为数据库系统、界面展示系统、分析诊断系统三大部分，完成数据存储、集成，数据分析，结果展示以及状态诊断功能。该系统能够与便携式信息采集系统通过通用串行数据总线通信，方便快速地实现数据转储。

4 导线张力测量系统构建

线路张力测量基于“三点弯曲法”，更具被测导线受力和变形的特点，考虑拉弯刚度对测量信号的影响，利用“纵横弯曲”的原理，建立线路张力计算模型[17]。本文对选用“旁压式”张力传感器测量导线张力情况，该传感器安装于带测线路时，强迫线路产生弯曲变形，见图7，C相对于支座A和B向下压紧导线，产生位移信号δ和压紧力P。通过对该信号的处理，得到张力的表达式，从而间接获得导线轴向拉力值[17]。

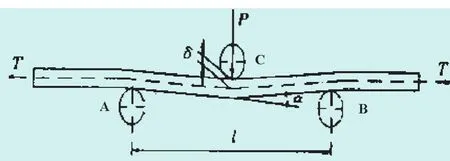
图7 张力传感器原理Fig.7 Principle diagram of tension sensor

本文采用旁压式张力传感器进行张力测量，首先对其特性进行了校准，方法为通过拉力机对导线施加一定张力，认为该数值为准确张力值，同时采用旁压式张力传感器对该张力信号进行同步测量，实验方法如图8所示，实验结果如图9所示。

图8 张力传感器校准方法Fig.8 Calibration method for tension sensor

根据图9，可知拉力机测量结果与张力传感器测量结果具有类似线性的关系，因此将两信号做比值运算，即得到张力传感器校准曲线，如图6。

根据图10，拉力机张力超过10 kN时，拉力机数值与张力传感器数值之比稳定在1.4左右，认为张力传感器输出处于线性区，可直接用于张力测量；拉力机张力小于10 kN时，该比值线性度差，可根据该校准曲线，通过插值算法获得真实张力值。

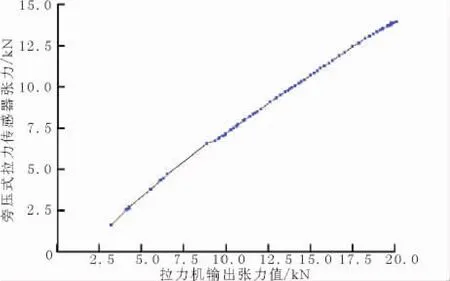
图9 张力传感器实测数据Fig.9 Data of tension sensor measured

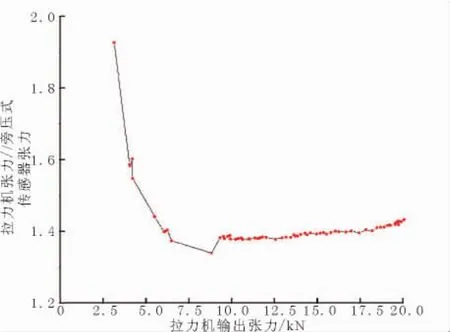
图10 张力传感器校准曲线Fig.10 Calibration curve diagram of tension sensor

5 实测与分析

5.1 实验线路参数

试验用导线为符合GB1179-1983的钢芯铝绞线，线路参数如表1所示。架空线长65 m，弧垂小于0.5 m，垂跨比小于1：130，适合采用张力与振动理论模型进行分析。

表1 实验线路参数Tab.1 Experiment wire parameters

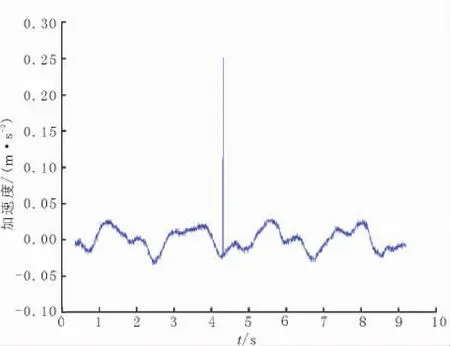
图11 水平横向振动信号Fig.11 Signal of transverse vibration in wire

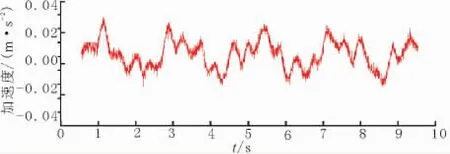
图12 面内垂直振动信号Fig.12 Signal of in-plane vertical vibration in wire

5.2 实测数据

采用本文设计的振动检测系统对实验线路进行实际测量，图11为微风激励下测量点水平横向振动信号，图12为该测量点面内垂直振动信号。

采用旁压式张力传感器测得实验线路张力值为6 694 N，查询校准曲线，可知线路真实张力大小为9 180 N。

5.3 分析与讨论

对水平横向振动和面内垂直振动信号进行快速傅里叶变换，得到频谱分别如图13和图14所示。

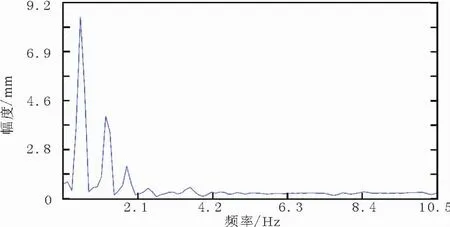
图13 水平横向振动频谱Fig.13 Spectrum of transversevibration in wire

提取振动频谱谱峰对应频率值，即可得到两种振动的各阶本征频率，如表2所示。

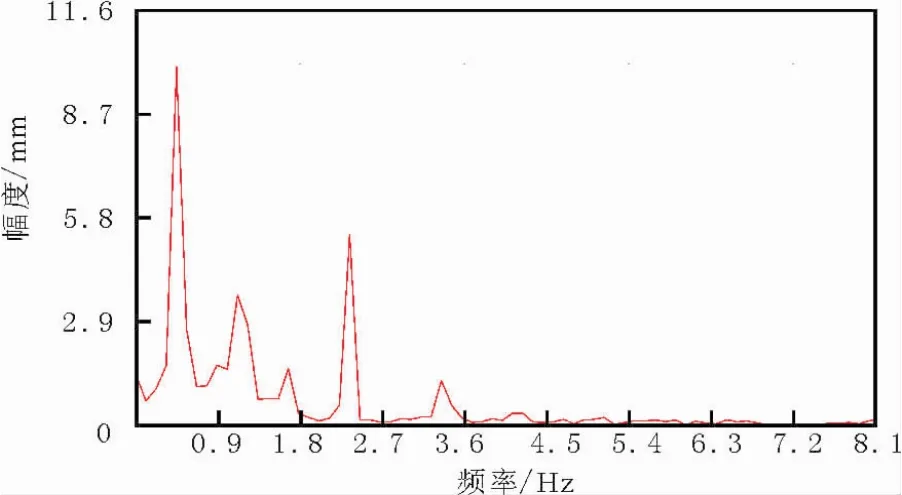
图14 面内垂直振动频谱Fig.14 Spectrumof in-planeverticalvibration for wire

对水平横向振动和面内垂直振动分别做本征频率与对应阶次的比值，考察是否存在频率漂移，得到表3。

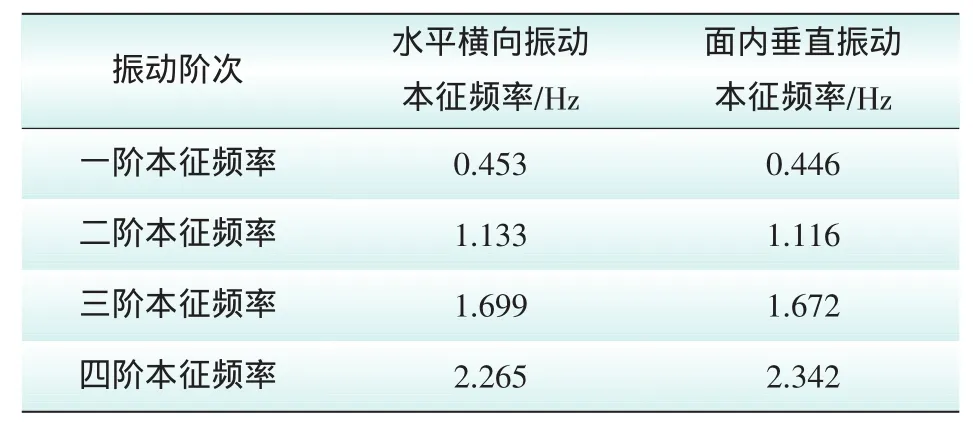
表2 导线振动频率分布Tab.2 Spectrum distribution for vibration for wire

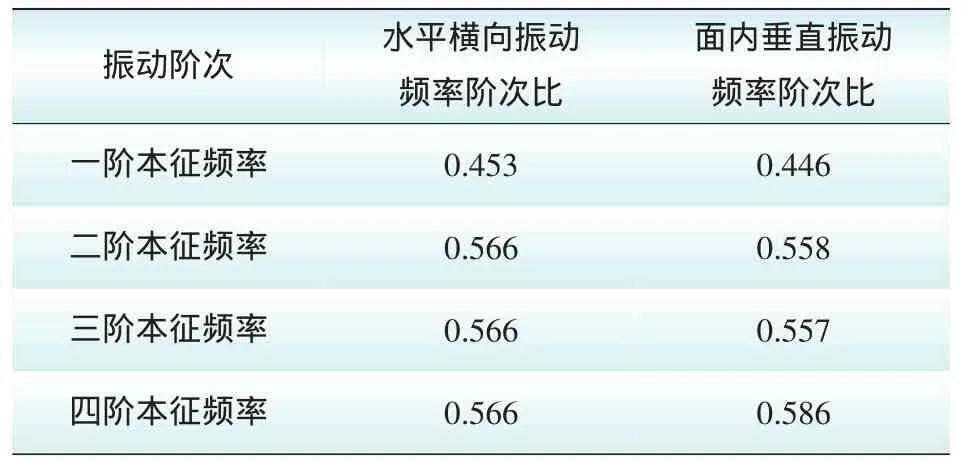
表3 频率阶次比分布Fig.3 Ratios of frequency than order for wire

对比图13和图14，架空导线受到微风激励时，水平横向振动低阶频率含量较高，随频率升高，各频率分量成分逐步降低；面内垂直振动各阶频率能量成分分布较为杂乱，在2.0 Hz左右出现一个尖峰，随后高阶分量成分基本消失。本文认为出现该现象的原因为对于水平横向振动，激励来源主要为水平方向风力，而面内垂直振动激励来源主要为微风吹拂引起的卡尔曼漩涡现象，其影响因素较多，故频成分较为复杂。

表3给出了2种振动频率阶次比，发现2种振动一阶频率阶次比普遍小于高阶频率阶次比，即一阶频率发生了频率漂移。本文认为出现该现象由线路结构特性引起，架空输电线路为多股绞合结构，线路振动时会发生股与股的相对位移，对于低阶振动，振动幅度大、能量高，因此股间相对位移较大而高阶振动股间相对位移较小，从而导致低阶振动消耗阻尼功率高于高阶振动；同时使导线抗弯刚度会随频率不同发生变化，对频率分布产生一定影响。

表3给出了2种振动频率阶次比，发现2种振动一阶频率阶次比普遍小于高阶频率阶次比，即一阶频率发生了频率漂移。本文认为该现象是由线路导线材料和结构特性引起；架空输电线路为多股绞合结构，线路振动时会发生股与股的相对位移，对于低阶振动，振动幅度大、能量高，因此股间相对位移较大而高阶振动股间相对位移较小，从而导致低阶振动消耗阻尼功率高于高阶振动；同时导线抗弯刚度会随频率不同发生变化，对频率分布也会产生一定影响；另外，对于导线的平面内振动，其各阶振动本征频率除受到导线材料和结构特性影响外，还会受到弧垂的影响，多种因素共同作用，导致频率特性发生改变。

6 结论

本文采用频谱法实现架空输电线路导线张力的间接测量，搭建了线路振动信息测量系统。该系统由张力测量与传输系统，便携式信息采集系统和上位机综合分析系统构成，能够有效实现对待测线路小干扰、无损伤的振动检测。

基于本文开发的测量系统，对实验线路进行了实际测量，得到了线路振动加速度信号，同时采用张力测量传感器，得到了对应的张力数据。采用小波分析对振动信号进行了降噪处理，能够减小信号干扰，有利于特征信息的提取。进而对数据进行了分析，采用快速傅里叶变换（FFT）得到线路振动频谱，采用前两阶本征频率数据，验证了振动频谱与张力关系模型。通过实测证明，基于振动频谱原理的导线应力测试方法是可行的，可取代传统的架空线路张力检测工具。

[1] 黄剑波,吴开贤.输电线路雨雪冰冻灾害研究 [J].电网与清洁能源,2008(9):24-28.HUANG Jian-bo,WU Kai-xian.Research on disaster of snow storm and frozen rain for power transmission line[J].Advances of Power System&Hydroelectric Engineering,2008(9):24-28(in Chinese).

[2] 韩军科,杨靖波,杨风利,等.电网冰灾典型线路段覆冰倒塔分析[J].电网与清洁能源,2010,26(3):31-35.HAN Jun-ke,YANG Jing-bo,YANG Feng-li,et al.Analysis on tower collapsing for ice coating on typical transmission line in power grid ice disaster area[J].Advances of Power System&Hydroelectric Engineering,2010,26(3):31-35(in Chinese).

[3] 苏成,徐郁峰,韩大建,等.频率法测量索力中的参数分析与索抗弯刚度的识别[J].公路交通科技,2005,22(5):75-78.SU Cheng,XU Yu-feng,HAN Da-jian,et al.Parameter analysis and identification of bending stiffness of cables during tension measurements by frequency method[J].Journal of Highway and Transportation Research And Development,2005,22(5):75-78(in Chinese).

[4] MEHRABI A B,CIOLKO A T.Health monitoring and problem solving for cable supported bridges[C].Strait Crossings,Bergen,Norway,2001,2001:55-60.

[5] 李宗凯.基于实测振动特性识别拉索索力的研究[D].北京：北京工业大学,2009.

[6] 程志军.架空输电线路静动力特性及风振研究[D].杭州：浙江大学,2000.

[7] 杨立秋,李海花,高玉竹.架空输电线路微风振动危害分析[J].中国科技信息,2008(12):54-55.YANG Li-qiu,LI Hai-hua,GAO Yu-zhu.The analysis of harmfulness about aeolian vibration on transmission line[J].China Science and Technology Information,2008(12):54-55(in Chinese).

[8] 周海滨,董明,郑雷,等.基于振动频谱机理的架空输电线路张力检测系统设计与开发[C]//高电压技术年会,济南,2011:413-451.

[9] VECCHIARELLI Jack.Aeolian vibration of a conductor with a stockbridge-type damper[D].Canada：University of Toronto,1997.

[10]杨玉金.线路大跨越微风振动在线监测系统的研究[D].合肥：合肥工业大学,2007.

[11]王洪.大跨越架空输电线路分裂导线的微风振动及防振研究[D].北京：华北电力大学,2009.

[12]IRVINE H M，CAUGHEY T K.The linear theory of free vibrationsof asuspended cable[C]//Proc Roy Soc Lond:Ser A,1974,341:299-315.DOI:10.1098/rspa.1974.0189.

[13]孔德怡,李黎,龙晓鸿,等.特高压架空输电线微风振动有限元分析[J].振动与冲击,2007,26(8):64-67.KONG De-yi,LI Li,LONG Xiao-hong,et al.Analysis of aeolian vibration of uhv transmission conductor by finite element method[J].Journal of Vibration and Shock,2007,26(8):64-67(in Chinese).

[14]王松平,陈笃.均匀和风作用下输电线振动分析[J].武汉汽车工业大学学报,1997(3):72-76.WANG Song-ping,CHEN Du.Analysis of transmission line vibration under well distributed breeze loads[J].Journal of Wuhan Automotive Polytechnic University,1997(3):72-76(in Chinese).

[15]段波,曾德荣,卢江.关于斜拉桥索力测定的分析[J].重庆交通学院学报,2005,24(4):6-8,12.DUAN Bo,ZENGDe-rong,LU Jiang.Analysis with determining cable tension of cable-stayed bridges[J].Journal of Chongqing Jiaotong University,2005(4):6-8,12(in Chinese).

[16]吴康,刘克明,杨金喜.基于频率法的索力测量系统[J].中国公路学报,2006(2):62-66.WU Kang,LIU Ke-ming,YANGJin-xi.Measuring system ofcabletensionbased onfrequencymethod[J].China Journal of Highway and Transport,2006(2):62-66(in Chinese).

[17]姚文斌,张蔚.斜拉桥张拉索张力的测定[J].传感技术学报.2004,17（3）:484-487.YAO Wen-bin,ZHANAG Wei.Determination of cable tension on cable-stayed bridge[J].Chinese Journal of Sensors and Actuators,2004,17(3):484-487(in Chinese).