原动机周期性扰动引发强迫功率振荡特性研究
2012-10-22董超云雷刘涤尘廖清芬占才亮汪如松王强
董超,云雷,刘涤尘,廖清芬,占才亮,汪如松,王强
(1.广东电网公司电力调度控制中心,广东广州510600;2.武汉大学电气工程学院,湖北 武汉 430072;3.中南电力设计院,湖北 武汉 430072)
保障电网安全高效运行是建设智能电网的主要目标之一。我国东北、华北、西北、华东、华中、南方等6个大型区域电网已通过交直流线路实现大范围互联,位于“三北”和西南地区的大电源基地数亿kW的功率需要通过大电网跨区输送到逾千km之外的东南沿海负荷中心。大型水电、火电集中外送系统中存在的功率振荡是中国能源外送面临的突出难题[1]。
近年来,我国电网多次发生未明机理的低频振荡事件。如1997年底河北南网500 kV安保线上大幅度的功率低频振荡,2008年华中电网广域测量系统(WAMS)记录到一次低频振荡事件,振荡波及范围广泛,等等[2-5]。在这些振荡发生前,电网都没有明显的故障和大的操作,因而振荡起因很不明确。通过模态分析和时域仿真发现采用传统的负阻尼机理不能很好的解释此次低频振荡事件,事后通过模态分析和时域仿真发现,采用传统的负阻尼机理不能很好的解释此次低频振荡事件,事后通过大量仿真分析和振荡复现,认为可能是由于系统存在外施周期性小扰动引发的强迫功率振荡。
原动机调速系统的周期性功率扰动可能会引起大范围内的强迫振荡。文献[6]指出,电力系统中原动机功率和负荷的持续周期性扰动由于共振均可能引起联络线的大幅度强迫功率振荡,但原动机机械功率扰动可能性更大,并且引起电网功率振荡的幅值也较大。文献[7]详细研究了二汽自备电厂2号机组调速器对华中电网低频振荡的不利影响,该机组调速器本身的不稳定,使其在系统有扰动时极易介入,与系统固有低频振荡共振,从而形成大幅度不衰减振荡。文献[8]指出,扰动源可能存在于汽轮机环节中,控制阀和主蒸汽压力如果发生周期性的波动,会导致汽轮机输出功率发生同频率波动,有可能导致系统发生大幅度的强迫功率振荡。
持续的周期性小扰动会引发电力系统强迫振荡,或称为共振机理的低频振荡。前期大量研究表明,它具有起振快、起振后保持等幅同步振荡和失去扰动源后振荡很快衰减等特点,且具有明确的扰动源[9-16]。因此有必要对原动机调速系统引发的强迫功率振荡进行研究。如果能够通过扰动源的相关性质及时发现其所在位置,则对于消除振荡具有重要的指导意义。
本文以大电源集中外送系统为背景建立仿真平台,结合计及原动机调速系统的Phillips-Heffron模型,通过转矩分析,给出判断原动机调速系统是否为强迫振荡扰动源的判据;另一方面,分析强迫振荡时发电机节点的能量变化特性,由不同的能量变化趋势区分扰动机组和非扰动机组。实际应用中,可以结合这2种方法综合定位强迫振荡扰动源。
1 转矩
计及原动机调速系统的Phillips-Heffron模型如图1所示。在图1的Phillips-Heffron模型中仅考虑增量的发电机组转子运动方程为
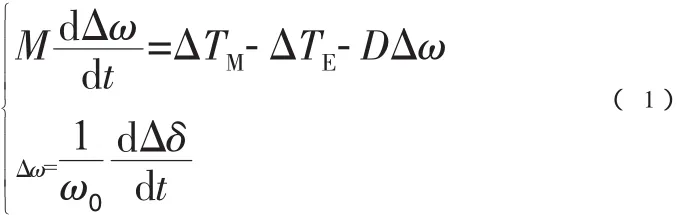
式中,△δ为功角变化量;△ω为转速变化量;△TM为机械转矩变化量;△TE为电磁转矩变化量;D△ω为阻尼项;ω0为系统基准角频率。
对式(1)的第二式进行拉普拉斯变换,有

将s=jωd代入式(2)得

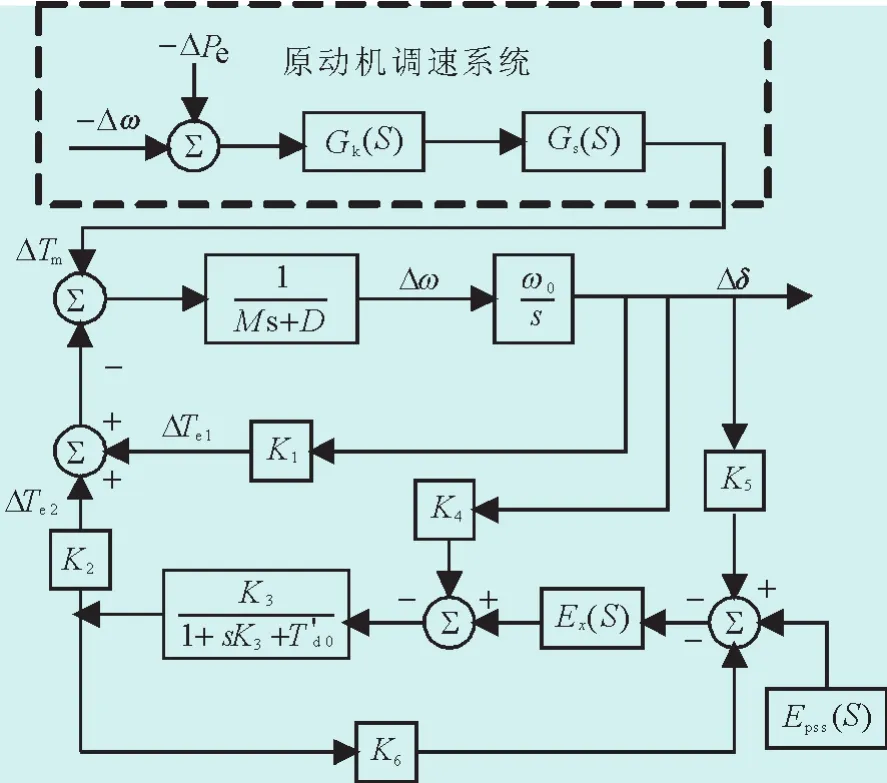
图1 包含原动机调速系统的Phillips-Heffron模型Fig.1 Phillips-Heffron model with turbine governor
为了分析方便,建立△δ-△ω坐标系,在该坐标系中分析机械转矩对低频振荡的影响。在复数平面内,式(3)中△ω与△δ正交,且△ω在相位上超前△δ的角度为90°。转子运动方程式(1)中阻尼系数D>0起正阻尼作用,D△ω投影在△ω的正半轴,在△δ-△ω坐标系的位置如图2所示。
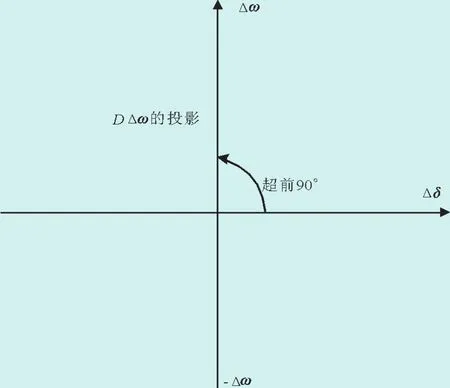
图2 D△ω在△δ-△ω坐标系内的投影Fig.2 Projection of D△ω in△δ-△ω coordinates system
阻尼系数D又称阻尼转矩系数,可以理解为单位转速变化下输出转矩的变化量,阻尼的存在使振动系统的运动状态处于衰减振动。阻尼转矩分量D△ω表示对转子运动的阻尼,未包含△TM以及△TE,是其他反对转子速度变化的转矩的总和,D>0,则阻尼转矩分量D△ω是正阻尼转矩,处于△ω的正半轴上。阻尼转矩D△ω与△ω成正比例关系,它只在△ω轴上有投影。
Phillips-Heffron模型中,原动机调速系统提供的机械转矩增量△TM的表达式为
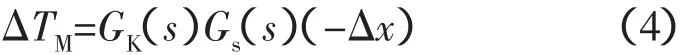
△TM还可以用式(5)形式描述

式中,△TS为同步转矩增量;△TD为阻尼转矩增量。
将式(5)代入(1)有
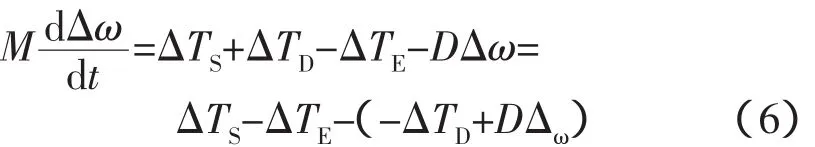
式中,D△ω的投影在△ω正半轴,当△TD与D△ω有相同性质,即原动机调速系统所产生的阻尼转矩分量△TD投影在△ω的正半轴时,-△TD投影在△ω的负半轴上,-△TD的作用与阻尼项D△ω的作用相反,原动机调速系统给系统提供负的阻尼。△TD与D△ω有相反性质即原动机调速系统所产生的阻尼转矩分量△TD投影在△ω的负半轴时,原动机调速系统给系统提供正的阻尼。其物理意义是:机组的机械输入转矩是加速转矩,设电力系统受到扰动后,机组出现一个与△ω轴正方向同相速度增量,此时,如原动机调速系统调节作用的结果也产生一个与△ω轴正方向同相的输入转矩增量,那么速度的增量就会进一步增大而不是减小,调速系统的作用就是负阻尼作用;相反,如果调速系统调节作用的结果产生一个与△ω轴正方向反相的输入转矩增量,那么速度的增量就会被减小,调速系统的作用就是正阻尼作用[17-18]。
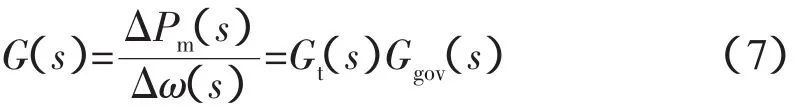
将s=jωd代入式(7),ωd=2πfd,fd为振荡频率,即可得到
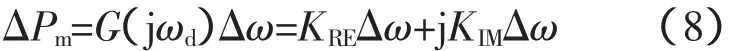
按照阻尼转矩与同步转矩分析的理论,KRE△ω是影响系统阻尼特性的分量。KRE>0时,△Pm中含有和△ω同相位的分量,根据发电机的转子运动方程,这个分量对系统的阻尼特性是不利的,原动机及其调速系统产生了负阻尼。KRE<0时,原动机及其调速系统产生正阻尼,因此,KRE△ω为负阻尼转矩,KRE称为机械负阻尼转矩系数。
因此可由发电机的输出量计算出KRE,若KRE为较大正值,则说明原动机及其调速系统向系统提供了负阻尼,为可能的振荡扰动源。
2 能量
电力系统结构保留模型下的能量函数方法研究表明,系统的暂态能量由系统总动能VKE和总势能VPE组成,其中系统势能分布于网络中,为所有支路势能之和[19]。发电机的线性化转子运动方程为
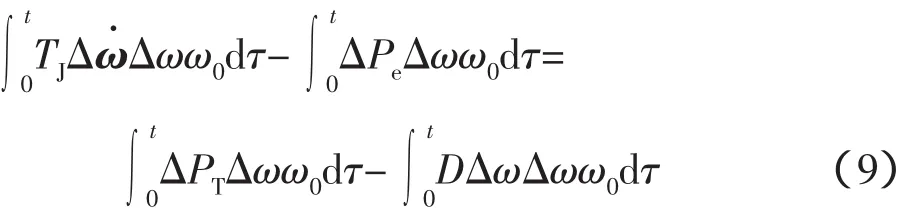
由式(9)可以定义线性化系统下能量函数的动能函数为
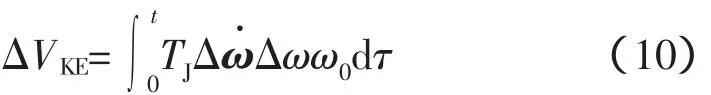
势能函数为
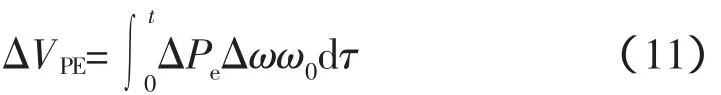
外施扰动注入能量函数为
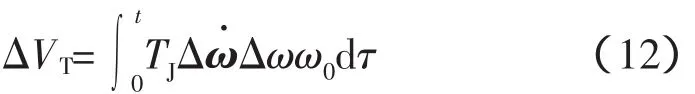
阻尼耗散能量函数为
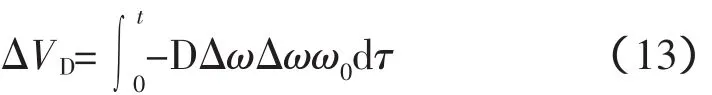
强迫功率振荡共振稳态情况下,系统外施扰动注入功率等于阻尼耗散功率,即扰动注入的能量与阻尼耗散的能量相等,动能和势能完全转换,总能量保持守恒,系统表现出类似于无阻尼自由振荡形式。
当某台发电机的原动机及其调速系统由于某种原因注入周期性振荡的功率时,发电机的动能将不可避免的发生增长,此时由于不平衡功率的产生,其他发电机的动能亦会被随之带动增。
3 仿真算例
3.1 单机无穷大系统
在单机无穷大系统中进行仿真分析,发电机采用如式(14)所示的3阶模型,不考虑励磁调节系统。系统频率为50 Hz,无穷大母线电压为1.0 pu,发电机母线与无穷大母线之间的连接电抗XL=0.8 pu,发电机参数Xd=0.146 0 pu,Xq=0.096 9 pu,X′d=0.060 8 pu,T′d0=8.96 s,Pm=1.0 pu,D=0.0,Efd=1.091 95 pu。
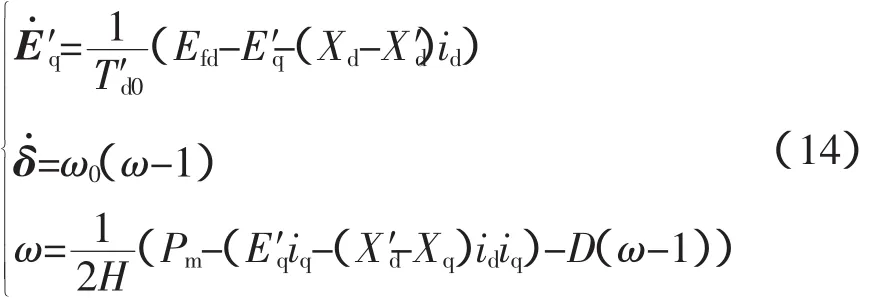
发电机的转动惯量为M=10 pu,无调速器时,计算的机电模式对应特征值-0.006 8+3.243 2j,fd0=0.516 2 Hz,ζ0=0.210%。不失一般性,以水轮机调速系统为例,其模型如图3所示,加入水轮机及调速器。水轮机调速系统采用文献[20]中的调速器模型,忽略死区和限幅,传递函数的框图如图3所示。其中参数采用文献[20]中给出的典型参数。Tp=0.05 s,Ks=5.0,TG=0.2 s,Rp=0.04,RT=0.4,TR=5.0 s。
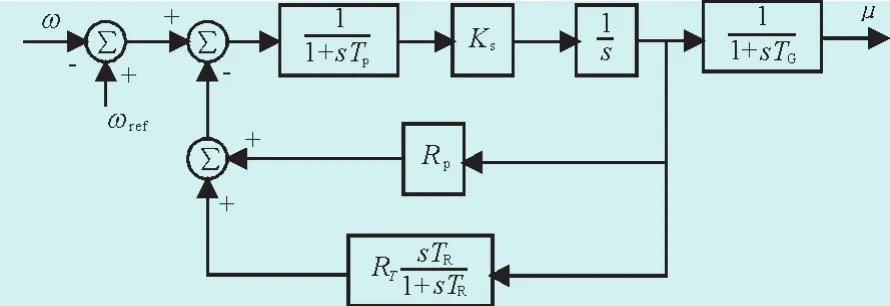
图3 水轮机调速器模型Fig.3 Hydro-turbine governor model
加入水轮机调速器模型后,计算所得特征值为0.026 8+3.207 4j,fd1=0.505 Hz,ζ1=-0.837% ,△ζ=-1.047%,特征值变化量为0.033 6~0.035 8j。
记系统的Jacobian矩阵为J。调速器的引入改变了Pm,根据△Pm=KRE△ω+j KIM△ω,同时考虑到s△δ=特征值发生变化。fd0=0.516 2 Hz时,计算得到G(jωd)=1.335 4-1.474 7j,KRE=1.335 4,KIM=-1.474 7。设矩阵J的特征值λ对应的左、右特征向量分别为Ψ、φ,且满足Ψφ=1,则特征值相对矩阵元素Jij的灵敏度为J22的灵敏度分别为

计算可得△Pm中2个分量导致的特征值变化分别为
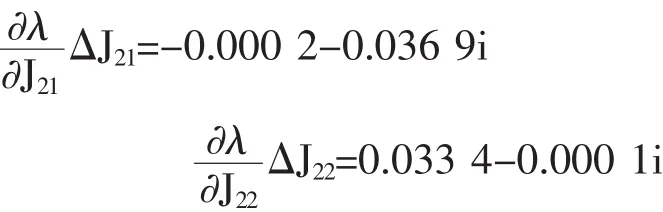
总的特征值变化量为0.033 2~0.036 9i,和实际的特征值计算结果很接近。分量KRE△ω主要改变实部,分量j KIM△ω主要改变虚部。上述分析也说明了原动机及其调速系统改变系统阻尼的机理。
3.2 简单系统1
以四机两区系统为基础[20],将母线10侧设置为无穷大系统,如图4所示。对该系统进行小干扰计算,得到系统的主导模式频率为0.334 Hz,对应阻尼比为0.436。G1设置原动机功率周期性扰动,为系统的强迫功率振荡扰动源,幅值为其额定功率的1%,频率为主导模式频率,持续时间为10~30 s,仿真时间为50 s。
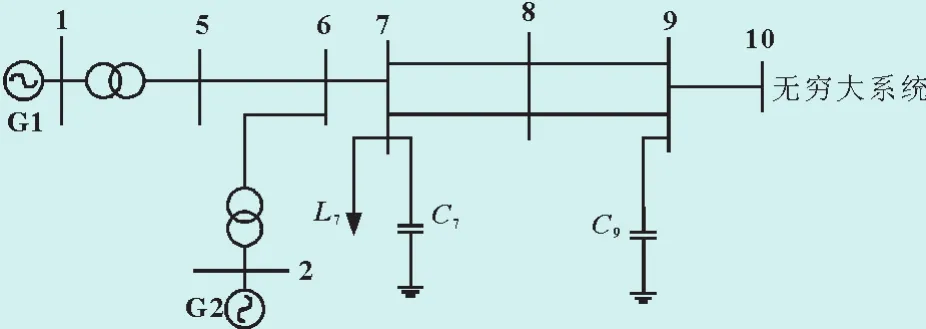
图4 简单系统1Fig.4 Simple system 1
对进入稳态后的功率偏差和功角偏差信号进行Prony分析,辨识得到的参数以及计算结果如表1所示。可得主导模式频率0.334 Hz下,G1的原动机及其调速系统阻尼转矩系数为正,也即起到恶化系统阻尼作用,为强迫功率振荡的扰动源;而G2的阻尼转矩系数为0,说明原动机及其调速系统对振荡基本不起作用。同理,对G2施加原动机周期性功率扰动,亦能够得到同样的分析结果,在此不再赘述。
采用能量方法求取发电机的动能、势能分别如图6、图7所示。
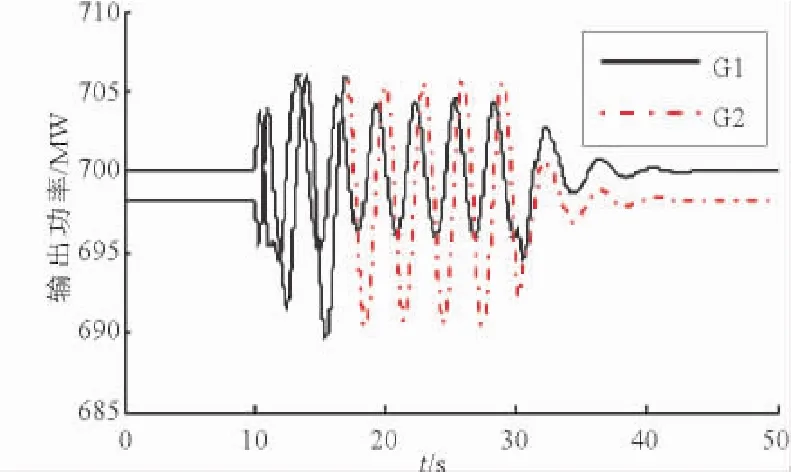
图5 机组有功功率振荡曲线Fig.5 Active power oscillation curve of units
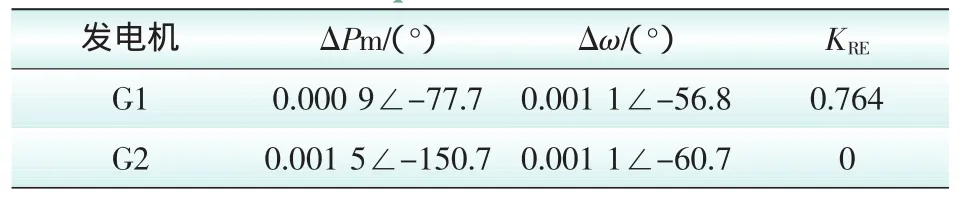
表1 参数辨识及阻尼转矩系数计算结果Tab.1 Resultsof parameters identification and damping torque coefficients
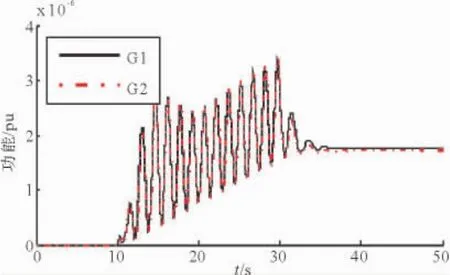
图6 机组动能变化曲线Fig.6 Kinetic energy curve of units
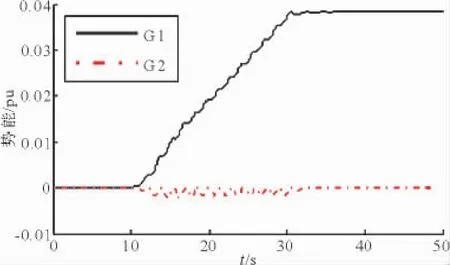
图7 机组势能变化曲线Fig.7 Potential energy curve of units
由于G1原动机及其调速系统存在周期性功率扰动,导致系统发生振荡,从而各台发电机的转子均在加速,因此其动能呈现持续增加状态;而由原动机功率扰动引发的强迫功率振荡,存在外施扰动的能量,扰动源所在机组的势能变化都与其他非扰动源机组相比存在明显的增长趋势,根据该特性也可以定位扰动源为G1机组。扰动源一旦切除,各发电机组动能和势能也将迅速达到新的平衡。
3.3 简单系统2
以8机36节点为基础[21],将母线1侧修改为无穷大系统,如图8所示。
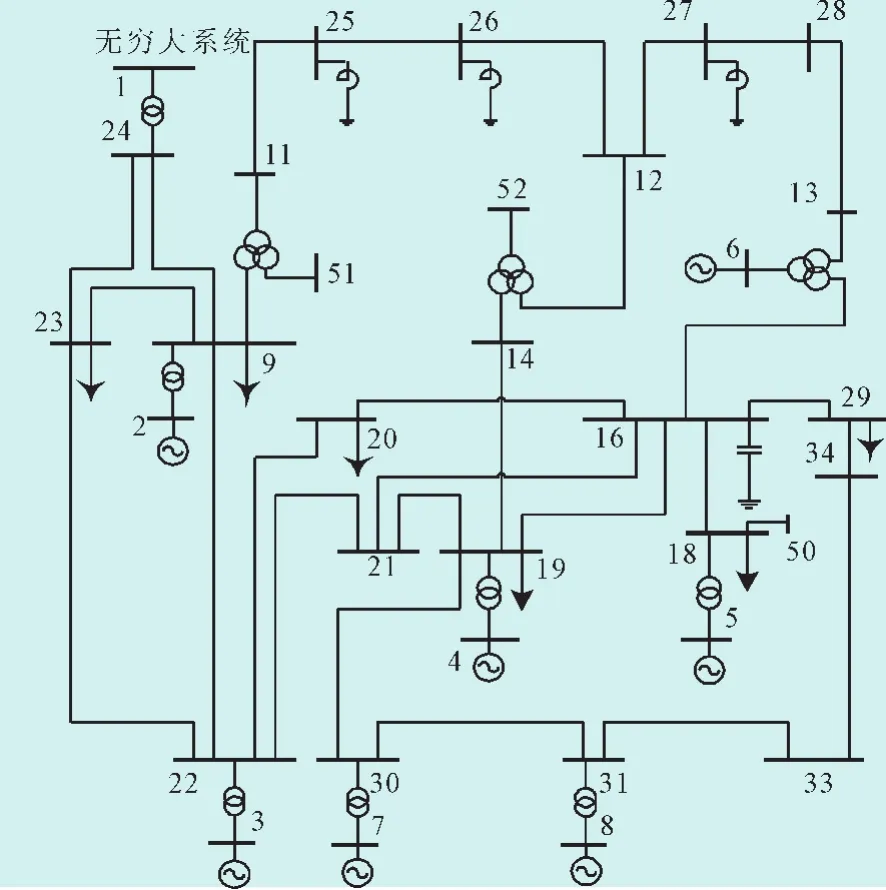
图8 简单系统2Fig.8 Simple system 2
对系统进行小干扰计算,得到系统的主导模式频率为0.564 Hz,阻尼比为0.862。设置G8的原动机功率周期性扰动,为系统的强迫功率振荡扰动源,幅值为其额定功率的1%,频率为主导模式频率,持续时间为0~20 s,仿真时间为40 s。对进入稳态后的功率偏差和功角偏差信号进行Prony分析,辨识得到的参数以及计算结果如表2所示。
由表2可见,G8的原动机及其调速系统阻尼转矩系数远大于其他发电机组,对系统强迫振荡的增助作用最大,根据该特性可以定位扰动源为G8机组。由于辨识精度和发电机组间的弱耦合原因,其他发电机组的KRE不完全为0,但与1.432相比足够小,可以近似视为0,对强迫振荡扰动源的定位没有影响。在实际应用中可以考虑设置阈值,各发电机组的KRE系数若与其中的最大值相比小于该阈值,则可以看作机组对系统的强迫振荡扰动源定位结果不起作用。
采用能量方法求取发电机的动能、势能分别如图9、图10所示。可以清楚看到各发电机组动能显著增加,施加扰动源机组势能与非扰动源机组有着明显区别,反映出G8机组为强迫功率振荡扰动源。对其他机组做相同仿真设置,亦可得到类似的结论。
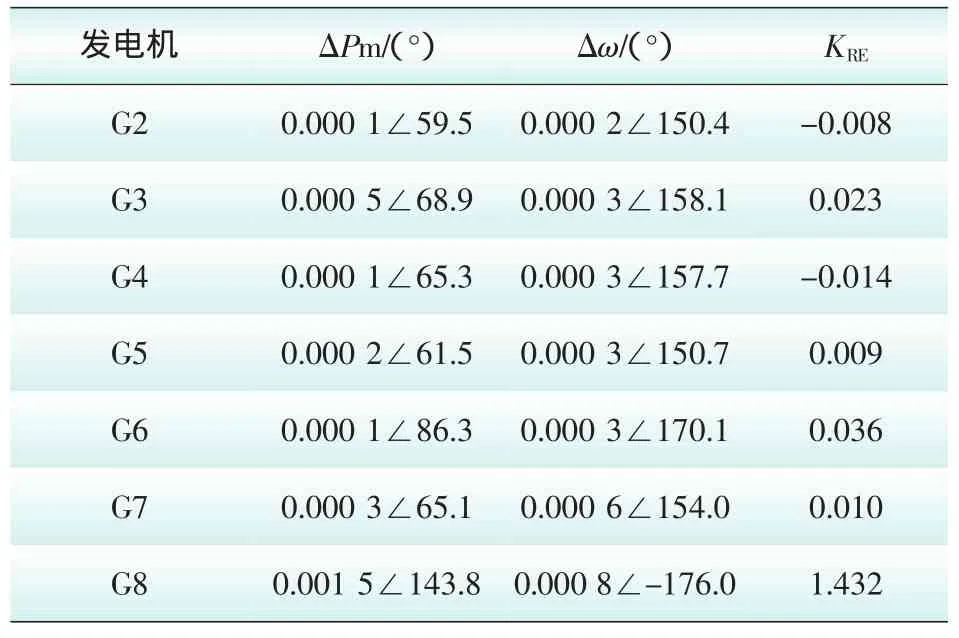
表2 参数辨识及阻尼转矩系数计算结果Tab.2 Results of parameters identification and damping torque coefficients
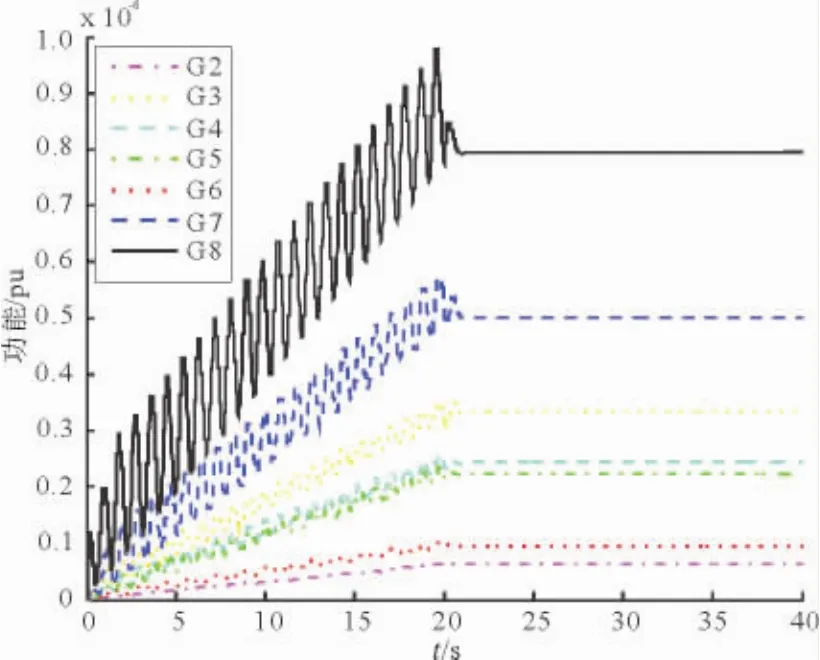
图9 机组动能变化曲线Fig.9 Kinetic energy curve of units
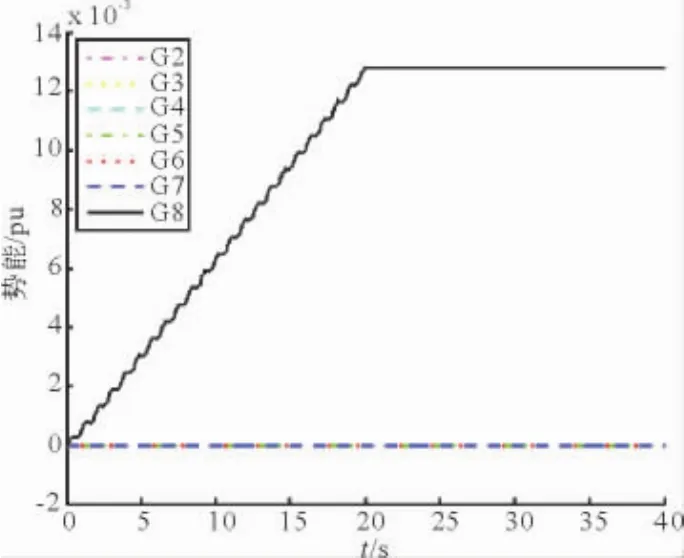
图10 机组势能变化曲线Fig.10 Potential energy curve of units
4 结论
1)通过分析计及原动机及其调速器的Phillips-Heffron模型,给出了机械负阻尼转矩系数KRE的计算公式以及物理意义,通过KRE能够判断原动机及其调速系统是否提供了振荡的负阻尼,从而为定位强迫振荡扰动源提供参考。
2)结合发电机经典二阶转子运动方程,利用能量方法计算发电机动能、势能。存在原动机及其调速器周期性功率扰动的机组,其势能会呈现明显不同于非扰动源机组的变化趋势,根据该性质能够快速辅助定位扰动源。
3)转矩方法和能量方法能够较好地描述原动机及其调速器类型的强迫振荡扰动源特性,综合这2种方法,可以较好地实现扰动源定位功能,为下一步发电机组的紧急控制或切除提供决策支持。
[1] 郭剑波.未来我国电网呈现三大特点[EB/OL].(2011-5-20)[2011-7-30].http://finance.jrj.com.cn/industry/2011/05/20151810018755.shtml.
[2] 王铁强,贺仁睦,王卫国,等.电力系统低频振荡机理的研究[J].中国电机工程学报,2002,22(2):22-26.WANGTie-qiang,HE Ren-mu,WANGWei-guo,et al.The mechanism study of low frequency oscillation in power system[J].Proceedings of the CSEE,2002,22(2):22-26(in Chinese).
[3] 杨东俊,丁坚勇,李继升,等.同步发电机非同期并网引起强迫功率振荡分析[J].电力系统自动化,2011,35(10):99-103.YANG Dong-jun,DING Jian-yong,LI Ji-sheng,et al.Analysis of power system forced oscillation caused by asynchronous parallelizing of synchronous generators[J].Automation of Electric Power Systems,2011,35(10):99-103(in Chinese).
[4] 文贤馗,王家胜.汽轮机侧引发的电网低频振荡分析[J].南方电网技术,2011,5(4):71-73.WEN Xian-kui,WANG Jia-sheng.Analysis of the lowfrequency oscillation of power grid caused by turbine sides[J].Southern Power System Technology,2011,5(4):71-73(in Chinese).
[5] 文贤馗,邓彤天,于东,等.汽轮机单阀-顺序阀切换造成电力系统振荡分析[J].南方电网技术,2009,3(2):56-58.WEN Xian-kui,DENGTong-tian,YU Dong,et al.Analysis of power systemoscillation by switchover of steamturbine's single and sequence valves[J].Southern Power System Technology,2009,3(2):56-58(in Chinese).
[6] 韩志勇,贺仁睦,马进,等.电力系统强迫功率振荡扰动源的对比分析[J].电力系统自动化,2009,33(3):16-19.HAN Zhi-yong,HE Ren-mu,MA Jin,et al.Comparative analysis of disturbance source inducing power system forced power oscillation[J].Automation of Electric Power Systems,2009,33(3):16-19(in Chinese).
[7] 王元虎.小机组调速系统引起的华中电网低频功率振荡分析[J].电网技术,1990,14(2):40-44.WANGYuan-hu.Analysis of LFOcaused by interaction of the speed governor of a small generator in central China power system[J].Power System Technology,1990,14(2):40-44(in Chinese).
[8] 徐衍会,贺仁睦,韩志勇.电力系统共振机理低频振荡扰动源分析[J].中国电机工程学报,2007,27(17):83-87.XUYan-hui,HERen-mu,HANZhi-yong.Thecauseanalysis of turbine power disturbance inducing power system low frequency oscillation of resonance mechanism[J].Proceedings of the CSEE,2007,27(17):83-87(in Chinese).
[9] 韩志勇,贺仁睦,徐衍会,等.基于能量角度的共振机理电力系统低频振荡分析[J].电网技术,2007,31(8):13-16.HAN Zhi-yong,HE Ren-mu,XU Yan-hui,et al.Analysis on power system low frequency oscillations originated in resonance mechanism from viewpoint of energy[J].Power System Technology,2007,31(8):13-16(in Chinese).
[10]竺炜,周有庆,谭喜意,等.电网侧扰动引起共振型低频振荡的机制分析[J].中国电机工程学报,2009,29(25):37-42.ZHU Wei,ZHOU You-qing,TAN Xi-yi,et al.Mechanism analysisof resonance-typelow-frequency oscillation caused by networks side disturbance[J].Proceedings of the CSEE,2009,29(25):37-42(in Chinese).
[11]韩志勇,贺仁睦,徐衍会.由汽轮机压力脉动引发电力系统共振机理的低频振荡研究[J].中国电机工程学报,2005,25(21):17-21.HAN Zhi-yong,HE Ren-mu,XU Yan-hui,et al.Power system low frequency oscillation of resonance mechanism induced by turbo-pressure pulsation[J].Proceedings of the CSEE,2005,25(21):17-21(in Chinese).
[12]韩志勇,贺仁睦,徐衍会.汽轮机压力脉动引发电力系统低频振荡的共振机理分析[J].中国电机工程学报,2008,28(1):47-51.HAN Zhi-yong,HE Ren-mu,XU Yan-hui,et al.Study on resonance mechanism of power system low frequency oscillation induced by turbo-pressure pulsation[J].Proceedings of the CSEE,2008,28(1):47-51(in Chinese).
[13]韩志勇,徐衍会,李志强,等.汽轮机调速系统引起电力系统共振机理低频振荡扰动分析[J].陕西电力,2009,37(7):1-5.HAN Zhi-yong,XU Yan-hui,LI Zhi-qiang,et al.Power system low frequency oscillation of resonance mechanism induced by disturbance of turbine-governing system[J].Shaanxi Electric Power,2009,37(7):1-5(in Chinese).
[14]余一平,闵勇,陈磊.多机电力系统强迫功率振荡稳态响应特性分析[J].电力系统自动化,2009,33(22):5-9.YU Yi-ping,MIN Yong,CHEN Lei.Analysis of forced power oscillation steady-stateresponsepropertiesin multimachine power systems[J].Automation of Electric Power Systems,2009,33(22):5-9(in Chinese).
[15]汤涌.电力系统强迫功率振荡的基础理论[J].电网技术,2006,30(10):29-33.TANG Yong.Fundamental theory of forced power oscillation in power system[J].Power System Technology,2006,30(10):29-33(in Chinese).
[16]鲍颜红,杨卫东,徐泰山.基于线性化模型的电力系统强迫功率振荡分析[J].江苏电机工程,2008,27(3):1-3.BAO Yan-hong,YANG Wei-dong,XU Tai-shan,et al.Analysison power systemforced power oscillation originated in linear model[J].Jiangsu Electrical Engineering,2008,27(3):1-3(in Chinese).
[17]王官宏,黄兴.汽轮机调速系统参数对电力系统阻尼特性的影响[J].电力自动化设备,2011,31(4):87-90.WANG Guan-hong,HUANG Xing.Influence of turbine governor parameters on power system damping[J].Electric PowerAutomationEquipment,2011,31(4):87-90(inChinese).
[18]王官宏,陶向宇,李文锋,等.原动机调节系统对电力系统动态稳定的影响[J].中国电机工程学报,2008,28(34):80-86.WANG Guan-hong,TAO Xiang-yu,LI Wei-feng,et al.Influence of turbine governor on power system dynamic stability[J].Proceedings of the CSEE,2008,28(34):80-86(in Chinese).
[19]余一平,闵勇,陈磊,等.基于能量函数的强迫功率振荡扰动源定位[J].电力系统自动化,2010(5):1-6.YU Yi-ping,MIN Yong,CHEN Lei,et al.Disturbance source location of forced power oscillation using energy functions[J].Automation of Electric Power Systems,2010(5):1-6(in Chinese).
[20]KUNDUR P.Power system stability and control[M].New York:McGraw-Hill,1994.
[21]蔡国伟,杨德友,张俊丰,等.基于实测信号的电力系统低频振荡模态辨识[J].电网技术,2011,35(1):59-65.CAI Guo-wei,YANG De-you,ZHANG Jun-feng,et al.Modeidentificationofpowersystemlow-frequencyoscillation based on measured signal[J].Power System Technology,2011,35(1):59-65(in Chinese).
