基于层级模型的嵌套型公共设施选址问题研究

万 波，杨 超，黄 松，董 鹏

（1.华中科技大学 管理学院，湖北 武汉 430074；2.江汉大学 档案馆，湖北 武汉 430056）

随着社会的进步，人们生活水平的提高，顾客对公共服务设施所提供的服务由“基本追求”、“求同”、“求异”向“优越性追求”、“自我满足追求”转化，顾客需求多样化程度越来越高［1］。因此，在进行公共服务设施规划时，需要对不同层级的公共服务设施进行科学选址，提供不同水平的服务，以满足顾客需求的多样性。

层级型设施选址问题涉及多级层次，且各层级之间的关系复杂，该问题引起了学者们的广泛关注。MOORE和REVELLE在最大覆盖选址模型中考虑了设施服务水平的多样性，建立了基于层级的最大覆盖选址模型（hierarchy maximal covering location model，HMCLM）［2］；TIEN 等根据不同层级设施提供的服务类型将设施分为嵌套型与非嵌套型，如果高级别设施的服务功能包含低级别设施的功能，且至少有一项功能是其独有的，则该类设施为嵌套型设施，如果不同级别的设施提供的服务不同，则该类设施为非嵌套型设施［3］；MARIANOV和SERRA基于集覆盖与最大覆盖选址模型，研究了拥塞系统的层级设施选址与分配问题［4］；GALVAO等提出了无容量约束的三级选址模型，并将其应用于巴西里约热内卢母婴医院的选址［5］，对有容量约束且考虑设施负载均衡的三级选址问题进行研究［6］；ŞAHIN 和 SÜRAL 对层级设施选址问题进行综述，将其按流模式、服务可用性、服务空间配置模式及选址目标等系统特征进行分类，并对层级设施选址模型与算法进行了概括与总结［7］；TEIXEIRA和ANTUNES提出带容量限制的层级中位模型，并就单一分配、就近分配与路径分配3种类型的空间分配模式进行了讨论［8］；RATICK等将成本因素引入基于层级的最大覆盖选址模型，对巴基斯坦科哈特县医疗设施选址问题进行了研究［9］；陈志芬等将应急避难场所划分为临时、短期和中长期3个等级，建立了三级层次选址模型，并通过模拟实验对模型的效果进行了检验［10］；万波等对非嵌套型的学校层级选址问题进行了研究［11］。

以上研究多集中于非嵌套型设施，对嵌套型设施研究较少。且上述研究基本上按照距离分配，忽略了设施的外部环境、道路交通状况和所提供的延伸服务等多种因素的影响。笔者引入分段效用函数，在基于层级的最大覆盖选址模型（HMCLM）的基础上提出基于层级模型的嵌套型公共设施选址模型（public pacility location model based on nested hierarchy，PFLMNH），并利用遗传算法对该模型进行求解。

1 模型的建立

1.1 研究背景

根据消费者需求层级来考虑，设施选址的最典型问题为不同层级的医院类设施的选址问题。因此，笔者选取不同层级的医院类公共服务设施选址问题进行研究。

根据我国特殊国情，笔者考虑的医疗系统具有需求层次的多样性与服务设施的层级性特点。由于人体存在差异性，每个人健康状况、受教育程度、收入水平等情况不一样，致使对就医存在不同水平的需求。需求层次的多样性决定了服务设施的层级性，即需要建立多种层级的医疗设施，以满足各种层级的需求。

此外，医疗系统需要考虑公平性与效率。医疗服务的公平性体现在基本医疗卫生服务的可及性，即建立覆盖全体人民的基本医疗服务体系。系统效率体现为成本与效用的均衡，需要寻求系统服务效用最大化与运行成本最小化之间的均衡。

1.2 符号定义与参数说明

I为需求点的集合，每一需求点的需求水平分为多个等级，需求水平的集合用S表示。J为设施候选点的集合，为满足不同水平的需求，设施点所建设施具有层级性，且各层级设施所提供的服务具有嵌套性，设施的服务水平用t表示。为了使模型的描述更加清楚，将模型的有关参数定义如下:wis为需求点i关于s级水平需求的数量；bjt为定位于j点的t级水平的设施的最大容量；pt为t级水平设施的设置数目；uisjt为定位于j点的提供t级水平服务设施对于需求点i的s级水平需求的效用；dij为需求点i到设施候选点j的距离；cjt为定位于j点的t级水平设施的成本；Ast为t级服务水平的设施对于s级水平需求的引力因子；αs为引力敏感度参数；为对于s级水平需求而言，需求点i与设施点j的最小临界距离；为对于s级水平需求而言，需求点i与设施点j的最大临界距离。同时定义如下的决策变量:xisjt为源于需求点i的对于s级水平的需求分配给j点t级水平设施的份额；如果t级水平的设施定位于j点，yjt=1；否则为 0。

1.3 分段效用函数定义

效用是顾客对公共设施所提供服务的满意程度，是顾客选择设施的决定性因素。设施效用越大，顾客越倾向于选择该设施。笔者采用分段函数对效用进行描述。分段效用函数定义如下:

当dij≤时，效用完全由服务设施的吸引力决定，不受距离的影响；当＜ dij≤时，效用与距离呈线性递减关系；当dij＞时，效用为 0，不管设施如何提高吸引力水平，其效用都不会变化。

1.4 基于层级模型的嵌套型公共设施选址模型

笔者引入分段效用函数，参考基于层级的最大覆盖选址模型（HMCLM），建立了基于层级模型的嵌套型公共设施选址模型（PFLMNH）。该模型以追求系统效率最大化为目标，即系统的服务效用最大化，同时建设成本最小化，考虑服务水平的嵌套性、基本需求全覆盖、需求单一分配、效用优先分配及设施最大容量约束等条件。模型的目标函数及约束条件如下:

其中:式（1）表示系统的服务效用与建设成本的比值最大化，即系统的服务效率最大化；式（2）确保源于所有需求点的基本医疗水平的需求都能得到满足；式（3）表示一个特定水平的需求仅仅能被相应水平或者高水平的设施提供的服务所满足；式（4）表示每个服务设施点的最大容量限制；式（5）表示每一种水平的需求必须分配给效用最大的提供相同服务水平或者高水平的设施；式（6）表示决策变量的取值范围。

2 求解算法

利用遗传算法，根据预定的目标适应度函数对每个个体进行评价，依据适者生存和优胜劣汰的进化规则，不断得到更新的群体，同时以全局并行搜索方式来搜索优化群体中的最优个体，以求得满足要求的最优解［12］。求解算法步骤如下:

（1）编码并产生初始种群P0。采用整数编码，染色体结构由两部分构成，即选址编码与医院等级编码。选址编码部分中1表示相应的位置建立医院，0表示相应的位置不建立医院。医院等级编码中1表示建立一级医院，2表示建立二级医院，3表示建立三级医院。如图1所示，有5个候选点，第1、4点建立一级医院，第2点建立三级医院，第3点不建医院，第5点建立二级医院。随机产生N条染色体，构成一个初始种群P0。

图1 染色体结构

（2）染色体可行性操作。对随机产生的染色体和经过交叉、变异后的染色体进行修补，即修补那些选址方案中某一位为1而其对应的医院等级为0的染色体，将医院等级用随机产生的数（1，2，3）来替代。

（3）对需求点按效用进行分配。①将需求点分配给效用最大的且要建立的设施点；②对每个设施点计算分配到的需求量，判断是否超过设施点的容量，如果否，则将该需求点分配给该设施点，结束；如果是，则进行需求点的重新分配；③将因设施容量不足而未予以分配的需求点分配给其他设施点，分配原则是:与设施点效用次优且容量允许的待建设施点，否则分配给与设施点效用再次的且容量允许的待建设施点，依此类推。转步骤（2）。

（4）求初始种群P0的目标值。根据步骤（3）所得分配方案，求取相应染色体的目标值。

（5）交叉和变异，产生子种群Q0，求其目标值。

（6）将P0和子种群Q0合并，根据目标值排序，选取较优的N条染色体形成新种群R0。

（7）判断是否满足结束条件，如果否，转步骤（2）；否则结束。

3 案例研究

以武汉市某区为例，对该区医院选址问题分3种情景进行讨论。相关参数取值如下:

情景1:嵌套情况下的医院选址与分配情况分析。

（1）遗传算法的收敛性分析。由图2可知，遗传算法具有较好的收敛性，当迭代次数count=446时收敛，目标函数值收敛于13.637。

图2 嵌套情况下的迭代次数与目标函数值关系图

（2）医院选址与分配情况。医院的选址与分配情况如表1所示。

由表1可知，需建立6所一级医院，提供一级服务；建立4所二级医院，提供一级和二级服务；建立1所三级医院，提供一级、二级和三级服务。医院选址与分配情况充分体现了设施服务水平的嵌套性。为直观起见，仅列出一级需求的分配情况，如图3所示。由图3可知，编号为44的点因距离其他设施选址点较远，按照效用分配的原则，其与其他所有点的效用均为0，故在此点建立一级医院，满足其自身的一级需求。此外，编号为19的设施点由于其容量较大，且处于中心地带，故其分配到的一级需求点是最多的。

（3）需求级别与医院级别的匹配度分析。需求级别与医院级别的匹配情况如表2所示。

由表2可知，各级需求分配给不同级别医院的比例是不同的，同级需求分配给相应等级医院的比例是最高的，如一级需求分配给一级医院的比例为46%，高于分配给二级医院的42%与分配给三级医院的12%。这是由于分配采用效用优先原则，而效用是与设施的引力密切相关的，笔者设定需求级别与相对应的医院的引力因子最高，故居民首选到与需求水平相对应级别的医院看病。此外，一级需求的覆盖比例为100%，体现了基本医疗服务的公平性，即建立覆盖全体人民的基本医疗服务体系。同时，由于受财政预算约束等因素影响，二级需求与三级需求均未得到全覆盖，其覆盖比例分别为98%和65%。

表1 医院选址与分配情况一览表

图3 嵌套情况下的一级需求分配图

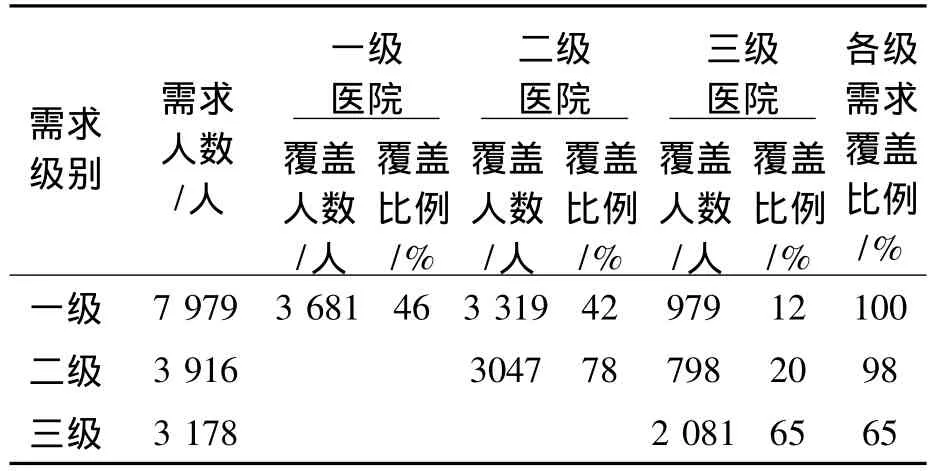
表2 各级需求点被各级医院覆盖情况一览表

情景2:按效用分配与按距离分配的情况比较。

将按效用优先与传统的按距离就近分配的情况进行比较，结果如表3所示。

表3 按效用分配与按距离分配结果对比

由表3可知，虽然各级医院数目没有发生变化，但医院选址与分配情况发生了明显的变化，这是由于按效用分配不仅考虑了距离，而且考虑了设施的吸引力，分配更加切合实际情况。另外，按效用分配时，模型的目标函数值较高，原因是按效用分配时，其系统效用为12819，明显高于按距离分配时的12468，在总成本不变的情况下，模型的目标函数值变大。因此，与传统的按距离分配比较，按效用分配有明显的优越性。

情景3:嵌套与非嵌套情况求解结果比较。

假设各级医院仅提供相应水平的服务，即医院类型为非嵌套型，现将非嵌套型求解结果与嵌套型进行比较，如表4所示。

表4 嵌套型设施与非嵌套型设施求解结果对比表

由表4可知，与嵌套的情况相比，非嵌套的情况下医院数目均发生了明显变化，就医院总数来讲，嵌套的情况比非嵌套的情况少7所，导致其总成本明显降低。同时，嵌套情况下的系统效用大，非嵌套情况下的系统效用小。因此，嵌套情况下的目标函数值明显高于非嵌套情况下的目标函数值，说明嵌套系统的服务效率明显高于非嵌套系统。这是由于嵌套系统设施提供服务的多样性，充分利用设施的使用效率所致。因此，在进行公共设施系统设计时，应尽可能考虑嵌套系统，提供多级别的服务，以实现系统的服务效率最大化。

4 结论

引入分段效用函数，参考基于层级的最大覆盖选址模型（HMCLM），提出了基于层级模型的嵌套型公共设施选址模型（PFLMNH），并利用遗传算法对公共服务设施选址问题进行求解。笔者以武汉市某区为例进行案例分析，结果表明，遗传算法对求解该模型具有较好的收敛性。从案例所讨论的3种情况来看，各级需求分配给不同级别医院的比例是不同的，同级需求分配给相应等级医院的比例是最高的；与按距离分配相比，按效用分配的目标函数值更高，即系统的服务效率更高，表明在建立模型时，按照效用分配具有明显的优越性；嵌套情况下的目标函数值明显高于非嵌套情况下的目标函数值，说明嵌套系统的服务效率明显高于非嵌套系统。因此，在进行公共设施选址规划时，应尽可能考虑建立嵌套系统，并基于效用优先原则进行分配，以实现系统服务效率最大化。

［1］崔迅，张瑜.顾客需求多样化特点分析［J］.中国海洋大学学报:社会科学版，2006（2）:27－30.

［2］MOORE G，REVELLE C.The hierarchical service location problem［J］.Management Science，1982，28（7）:775－780.

［3］TIEN J M，EL －TELL K，SIMONS G R.Improved formulations to the hierarchical health facility location －allocation problems［J］.IEEE Transactions on Systems，Man and Cybernetics，1983，13（6）:1128 －1132.

［4］MARIANOV V，SERRA D.Hierarchical location – allocation models for congested systems［J］.European Journal of Operational Research，2001（1）:195 －208.

［5］GALVAO R D，ESPEJO L G A，BOFFEY B.A hierarchical model for the location of perinatal facilities in the municipality of Rio de Janeiro［J］.European Journal of Operational Research，2002（3）:495 －517.

［6］GALVAO R D，ESPEJO L G A，BOFFEY B，et al.Load balancing and capacity constraints in a hierarchical location model［J］.European Journal of Operational Research，2006（2）:631 －646.

［7］ŞAHIN G，SÜRAL H.A review of hierarchical facility location models［J］.Computers ＆ Operations Research，2007，34（8）:2310 －2331.

［8］TEIXEIRA J C，ANTUNES A P.A hierarchical location model for public facility planning［J］.European Journal of Operational Research，2008（1）:92 －104.

［9］RATICK S J，OSLEEB J P，HOZUMI D.Application and extension of the moore and revelle hierarchical maximal covering model［J］.Socio － Economic Planning Sciences，2009，43（2）:92 －101.

［10］陈志芬，李强，陈晋.城市应急避难场所层次布局研究（Ⅱ）［J］.自然灾害学报，2010，19（5）:14 －19.

［11］万波，杨超，黄松，等.基于分级选址模型的学校选址问题研究［J］.工业工程与管理，2010，15（6）:16 －21.

［12］雷英杰，张善文，李续武，等.Matlab遗传算法工具箱及应用［M］.西安:西安电子科技大学出版社，2005:95－105.