光纤光栅振动传感器的振动理论分析

陈 帮，郭明金，王熙熙

（武汉理工大学光纤传感技术国家工程实验室，湖北 武汉 430070）

随着社会进步、经济发展和生活质量的提高，人们的安全防范需求也在不断增长。周界入侵报警系统作为安全防范的首要防线，目前主要采用主动红外入侵传感器［1－2］、微波对射入侵传感器［3－4］、激光对射传感器、振动传感电缆传感器［5］和泄漏电缆入侵传感器［6－7］，这些传感器的主要缺点是受气候环境的干扰较大，误报率较高。光纤干涉型振动传感器［8－10］虽然克服了上述传感器的缺点，但由于其原理的限制，不能对入侵的位置进行精确定位。而新型光纤布喇格光栅振动传感器［11］既保留了光纤振动传感器的抗电磁干扰、信息容量大和传输距离远等优点，又克服了不能精确定址的缺点，具有灵敏度高、响应时间短、误报和漏报率低等优点。基于光纤布喇格光栅振动传感器的周界入侵报警系统可广泛应用于机场、油库、核电站、军事基地、监狱外墙、住宅小区、银行金库、石油管道和高速公路隔离带等，是今后周界入侵报警系统发展的方向。

笔者着重从理论上分析了光纤布喇格光栅振动传感器的振动特性，将其近似为单质点的弦振动模型，对其进行等效刚度变换并等效为简单的弹簧－质量系统。首先确定系统的阻尼比，然后根据系统阻尼比计算出系统的最大振幅以及光纤长度的最大变化量，通过与丹麦BK公司生产的型号为7700的振动台测得的光纤长度实际最大变化量相比较，来检测弹性系数等效法是否准确。实验数据表明弹性系数等效法完全正确，且相对误差低，同时该分析方法简单，能为光纤布喇格光栅振动传感器在今后周界入侵报警系统中的应用提供理论支持。

1 光纤布喇格光栅振动传感器结构及模型

光纤布喇格光栅振动传感器的原理如图1所示。光纤两端固定，在布喇格光栅附近固定一质量块，质量块的尺寸为φ 5 mm×15 mm，材料为不锈钢基粉末冶金材料，最后用不锈钢或玻璃封装。

图1 光纤布喇格光栅振动传感器结构原理

由于光纤两端固定，且光纤的质量与质量块的质量相比完全可以忽略不计，可以把光纤作为没有质量，只有弹性的弹簧。因此光纤布喇格光栅振动传感器可近似为单质点的弦振动，如图2所示。质量块m=16 g，质量块m到端点的距离L=50 mm。

为简化模型便于分析，将单质点弦振动等效为纵向振动，如图3所示。设光纤的弹性系数为k1，等效弹性系数为k，实验测得系统的固有频率为20 Hz，由振动的固有频率f=，可得:

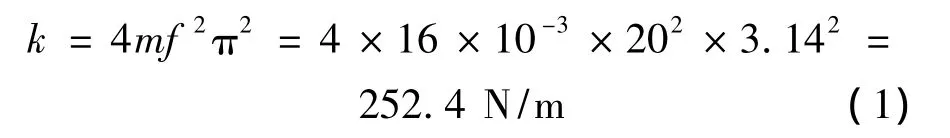
图2 单质点弦振动

图3 纵向振动

2 物理模型推导

2.1 具有粘性阻尼系统的受迫振动

无阻尼的自由振动只是一种假设状况，在实际中任何系统的振动都不可避免地存在阻力，因而自由振动都是会衰减的，振幅将随着时间而逐渐衰减，直至为0。由于粘性阻力与速度成线性关系，因此，为了简化振动问题的分析，通常假设系统阻尼为粘性阻尼。

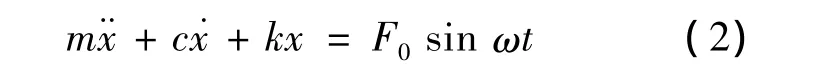
该微分方程式是一个二阶线性常系数非齐次微分方程。它的通解可以用二阶线性常系数齐次微分方程式的通解x1（t）和特解 x2（t）之和表示［13］，即:

其中:x1（t）为阻尼系统的自由振动，在小阻尼的情况下，x1（t）=Ae－ntsin（ωrt+φr）是一个衰减振动，只在开始振动后某一较短时间内有意义，随着时间的增加，将持续衰减，由于实验研究的是受迫振动中的等幅振动，故可以省去x1（t）；x2（t）为阻尼系统的受迫振动，称为系统的稳态解。从微分方程式非齐次项是正弦函数这一性质可知特解亦为正弦函数，它的频率与激振频率相同。因此可以设特解为:

Hd（ω）为位移频响函数，将x2（t）的一阶导和二阶导代入式（3）可得［14］:

从式（7）可以看出，具有粘性阻尼的系统受到简谐激振力作用时，受迫振动也是一个简谐振动，其频率与激振ω相同，振幅A、相位角φ取决于系统本身的性质（质量m、弹簧的刚度k、粘性阻尼系数c）和激振力的性质（加速度a、频率ω），而与初始条件无关。

2.2 系统的阻尼比

由式（6）可知，为了求出系统的振幅，必须求出系统的阻尼比ξ，通过对系统的频响进行分析，可以确定系统的阻尼比ξ。

为求幅频曲线峰值所对应的角频率ω1，可通过对式（6）求极值的方法来实现，令:

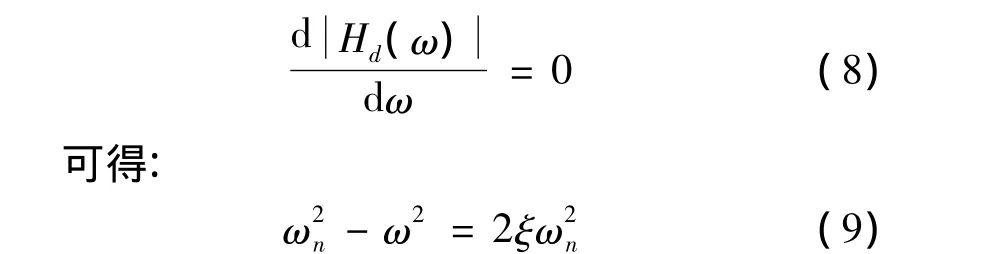
由式（9）解得:

由于一般工程结构的阻尼比都较小（ξ≤0.1），则可认为:ω1= ωn。由此可见，幅频特性曲线峰值对应的频率可以确定为系统的固有频率。即相频特性曲线在－90°处对应的频率为系统的固有角频率。

在半功率点处，频响函数的幅值可表示为［15］:

解式（11），可得到两个近似解:

易知，a、b两频率特性曲线所对应的相位分别为:

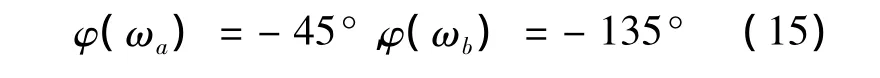
3 实验结果及分析

由式（10）～式（15）的分析可知幅频特性曲线在半功率点处以及相频特性曲线在 －45°和－135°处所对应的频率分别为 ωn、ωa和 ωb，按式（14）确定系统的阻尼比ξ。

系统位移频响函数的幅频和相频曲线如图4所示，系统的固有频率 ωn=20 Hz；ωa=18 Hz；ωb=22 Hz。

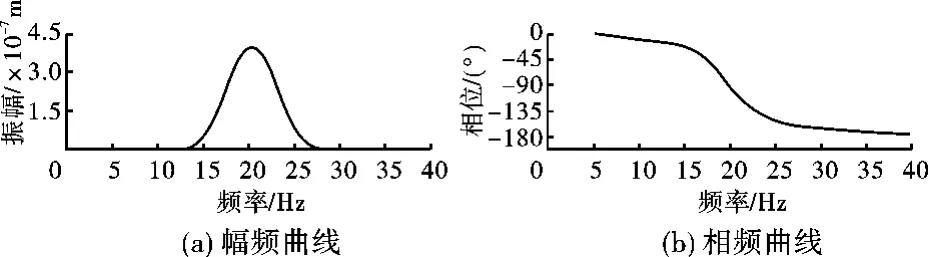
图4 系统位移频响函数的幅频和相频曲线

阻尼比为:

粘性阻尼系数为:

把k=252.4 N/m，c=0.4 N·s/m，F0=ma=16 ×10－3×3=0.048 N 代入式（6），有:

最大振幅时，光纤的长度变化量Δl1为:

对于有效弹光系数pe=0.22的石英光纤，易知［16］:ΔλB=0.78λBεx。

其中，λB为光纤光栅的反射中心波长（λB=1303.82 nm）；εx为光纤光栅的轴向应变，εx==7.81 ×10－5，则光纤光栅的中心波长变化量为:

光纤光栅中心波长变化图如图5所示。由图5可知，对光纤光栅振动传感器施加1～50 Hz的正弦扫频，施加的加速度为3 m/s2，扫频频率为1 kHz/s。实验所用的信号发生装置来自丹麦BK公司，其型号分别为:Heterodyne Analyzer Type2010、Power Amplifier Type 2719、Preeision Conditioning Amplifier TyPe2650、Vibration Exciter Type 4808；解调仪由武汉理工大学光纤中心自行研制。实际测得光纤光栅的中心波长变化量为70 pm（1303.89－1303.82=0.07 nm）。

图5 光纤光栅中心波长变化图

通过上述分析计算可知，光纤光栅的振动理论波长变化量为79.42 pm，实际测量的波长变化量为70 pm，虽然在同一个数量级，还是存在一定误差，产生误差的原因可能有:①测量所取的点较少，不能够全面反映光纤光栅的振动状况；②测量仪器有误差；③在理论建模过程中，忽略了很多变量，造成理论计算结果存在误差。

4 结论

实验通过弹性系数等效法，把单质点的弦振动等效为最简单的弹簧－质量系统，并分析了光纤布喇格光栅振动传感器的振动特性。理论计算光纤光栅的中心波长最大变化量为79.42 pm，实际测量的光纤光栅中心波长变化量为70 pm，在同一个数量级，能满足基于光纤布喇格光栅振动传感器的周界入侵报警系统的实际应用需要。

［1］LIDDIARD K C，GOODMAN G L.Versatile high － performance infrared intrusion sensor for remote surveillance applications［C］//Infrared Technology XXI.Part 1 of 2.United States:Society of Photo－ Optical Instru-mentation Engineers，1995:685 －695.

［2］SCHWARZ F.Performance of narrow － field，passive，infrared intrusion detector［C］//SPIE.Calif:Redondo Beach，1973:51 －56.

［3］MALYSHEV V M，PETROV A Y，VLADIMIROV A A.Mathematical model of microwave intrusion detector for perimeters［C］//2008 International Conference on Actual Problems of Electron Devices Engineering.United States:Inst of Elec and Elec Eng Computer Society，2008:249－254.

［4］MARTINEZ F P，GALEANO F C.New microwave sensors for intrusion detection systems［C］//Proceedings of the 1999 IEEE 33rd Annual International Carnahan Conference on Security Technology.United States:IEEE Piscataway，1999:49 －53.

［5］ACHKIRE Y，PREUMONT A.Optical measurement of cable and string vibration［M］.Amsterdam，Netherlands:IOS Press，1998:171 －179.

［6］HARMAN R K.Intrepid microtrack leaky cable sensor［C］//36thAnnual 2002 International Carnahan Conference on Security Technology.United States:Institute of Electrical and Electronics Engineers Inc，2002:191 －197.

［7］HARMAN K.Omnitrax ranging leaky coaxial cable sensor technology update［C］//43rd Annual 2009 International Carnahan Conference on Security Technology，ICCST 2009.United States:Institute of Electrical and Electronics Engineers Inc，2009:216 －220.

［8］JUAREZ J C，TAYLOR H F.Distributed fiber optic intrusion sensor system for monitoring long perimeters［C］//Sensors，and Command，Control，Communications，and Intelligence（C3I）Technologies for Homeland SecurityandHomelandDefenseIV.United States:SPIE，2005:692 －703.

［9］JUAREZ J C，MAIER E W，CHOI K N，et al.Distributed fiber－ optic intrusion sensor system［J］.Institute of Electrical and Electronics Engineers，2005，23（6）:2081－2087.

［10］RAO Y J，LUO J，RAN Z L，et al.Long － distance fiber－optic－OTDR intrusion sensing system［C］//20th International Conference on Optical Fiber Sensors.United States:SPIE，2009:7503 －7542.

［11］KAZAMA H，MITA A.FBG －based vibration sensor using gravity effects for large infrastructures［J］.Japan Society of Civil Engineers，2005，22（2）:159 －166.

［12］王梓坤.常用数学公式大全［M］.重庆:重庆出版社，1991:54－66.

［13］陈世民.理论力学简明教程［M］.北京:高等教育出版社，2001:14－26.

［14］王济，胡晓.MATLAB在振动信号处理中的应用［M］.北京:知识产权出版社，2006:33－81.

［15］龚善初.物理学与工程技术中非线性振动的常见求解方法［M］.北京:中国科学文化出版社，2006:23－42.

［16］姜德生，何伟.光纤光栅传感器的应用概况［J］.光电子·激光，2002，13（4）:420 －430.