Cymbal型压电换能器电压-位移特性建模与分析*
2012-10-21高全芹
高全芹
(长沙学院机电工程系,长沙 410003)
Cymbal型压电换能器[1-3]电压-位移特性[4]是其重要性能之一。目前对其研究手段有试验法[5]、有限元法[6-7]等,但这两种方法都无法给出能够描述电压-位移本质特性的函数模型。吴石林等[8]通过建立压电陶瓷圆片的压电方程,采用理论建模法分析了球帽Cymbal型换能器的位移特性。但吴石林将压电陶瓷片边界条件简化为自由边界状态,认为零应力约束。事实上压电陶瓷片端面受到Cymbal金属帽变形阻力约束,并非零应力约束。错误的边界条件导出的结论值得商榷。本文通过客观分析Cymbal换能器的压电陶瓷片所处于的受力约束状态,给出了压电方程的边界受力约束条件,建立Cymbal型压电换能器电压-位移函数关系模型。利用该模型可定量分析Cymbal型压电换能器结构敏感参数对其电压-位移特性影响规律。这些规律用于Cymbal型压电换能器批量生产中的性能一直性控制。
1 Cymbal压电换能器典型结构
典型的Cymbal换能器结构,如图1所示。上下Cymbal型金属端帽为对称结构,与压电陶瓷圆片严格胶合。与结构尺寸相关的变量有:端帽材料厚度t;端帽半径Rp;内腔椎底半径R1;内腔椎顶半径R2;压电陶瓷厚度为tp。
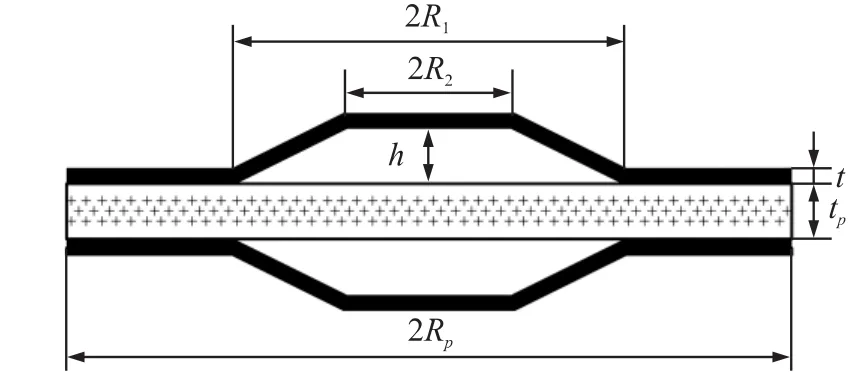
图1 Cymbal换能器结构
2 Cymbal换能器的压电方程
Cymbal型换能器轴向位移与压电陶瓷片的径向伸缩量和轴向伸缩量存在着一定的函数关系。计算压电陶瓷片的压电方程状态解是获得这一函数关系的有效途径。柱坐标下,Z轴极化的逆压电效应压电方程可表示为[3]:
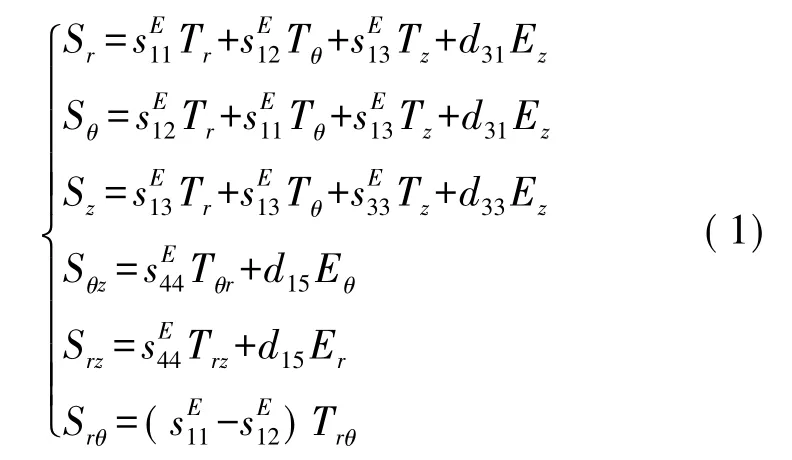

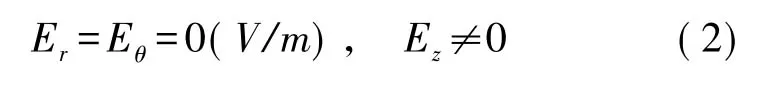
接下来必须对Cymbal换能器压电陶瓷圆片的受力状态进行分析,以确定其应力分量Tr、Tθ、Tz及Tzθ、Trz、Trθ值。
3 Cymbal换能器压电陶瓷片受力分析
当外加激励电场时,Cymbal换能器仅有轴向伸缩和径向伸缩运动,并无切向应变和切向应力,故可确定:

Cymbal换能器为旋转对称性结构,故可知沿径向方向的应力分量和应变分量相等,即:
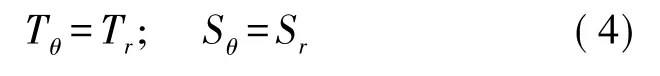
将式(2)、式(3)、式(4)代入式(1),得:
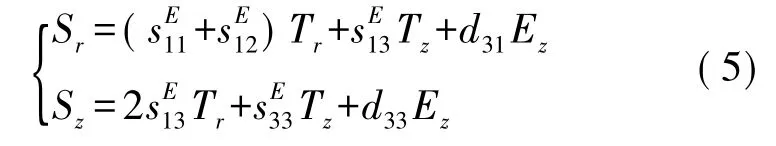
Cymbal换能器为旋转对称性结构,假设Cymbal型金属端帽与压电圆片沿圆周方向严格固联,当沿轴向对压电陶瓷圆片施加正向电场时,逆压电效应会驱使压电圆片沿径向方向产生收缩位移,将使Cymbal型金属端帽会发生弹性形变,产生轴向伸长位移,并同时产生阻止变形的弹性阻力。
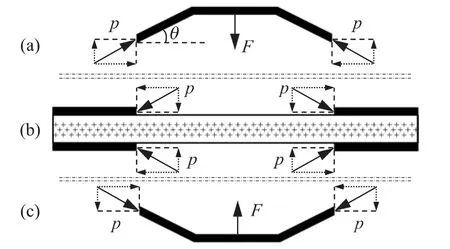
图2 Cymbal换能器分解受力示意图
如图2(a)所示,以Cymbal型金属端帽为分析对象,假设其由于形变产生的弹性阻力为F,压电圆对由于径向收缩位移对其产生的挤压作用力沿其底端沿圆周均匀分布,线应力大小为p,方向沿Cymbal型金属端帽母线方向。不考虑动态因素,则Cymbal型金属端帽受力平衡,有:

其中,θ=arctan(h/(R1-R2))。假设 Cymbal型金属端帽轴向伸长形变量为δz,由于δz为微小量,压电陶片径向变形在弹性范围内,因此,可将Cymbal型金属端帽视为碟形膜片弹簧,由 Almen-Laszlo[9]公式,可得:
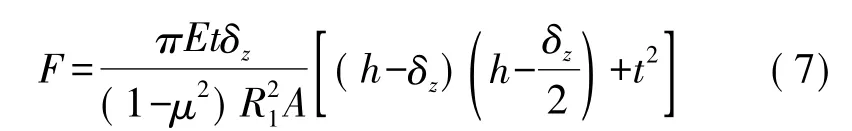
其中,A=6((R1-R2)/R1)/(πln(R1/R2))。如图 2(b)所示,设上下Cymbal型金属端帽完全相同,以压电陶瓷圆片为分析对象,则其受到上下金属端帽的反作用力p,根据材料力学知识,可得到压电陶瓷圆片应力Tr、Tz与线应力p之间的关系[10]:
·情感定位策略。情感定位是将人类情感中的关怀、牵挂、温暖、怀旧、爱恋等情感内涵融入到品牌中,使读者在参与活动的过程中获得这些情感体验,从而唤起读者内心的认同和共鸣。如对老年人群体体现陪伴与怀旧的情感,对儿童体现关爱的情感,对青少年或青年体现认同、激励的情感等。

假设压电陶瓷圆片沿径向方向上位移为Δr,轴向位移为 Δz,则有以下关系成立[11]:
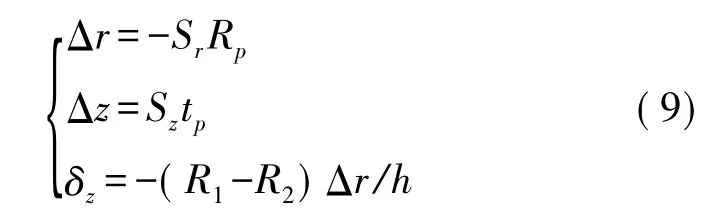
设Cymbal换能器轴向方向总位移为Δh,则有:

4 电压-位移特性函数描述方程
方程(5)~方程(10)联立,解得:
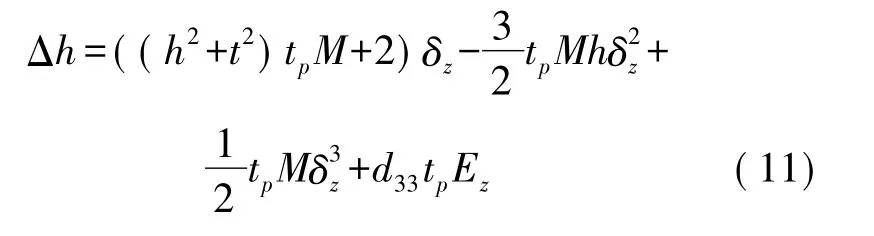


对于方程(10),电场强度Ez为唯一的自变量。当所加电场Ez确定条件下,可通过解三次方程实根方法精确计算出 δz,从而计算出 Δh,故Ez-Δh(电压-位移)特性曲线可惟一确定。
另外,小变形条件下,δz≤1,忽略二次以上高次项,则Ez-Δh近似线性公式:

5 电压-位移特性函数模型验证
Cymbal换能器的等效压电常数de33是描述其电压-位移特性的重要参数之一。de33定义为:

Cymbal换能器的等效压电常数de33通常可由试验方法直接测得。取样机参数为:
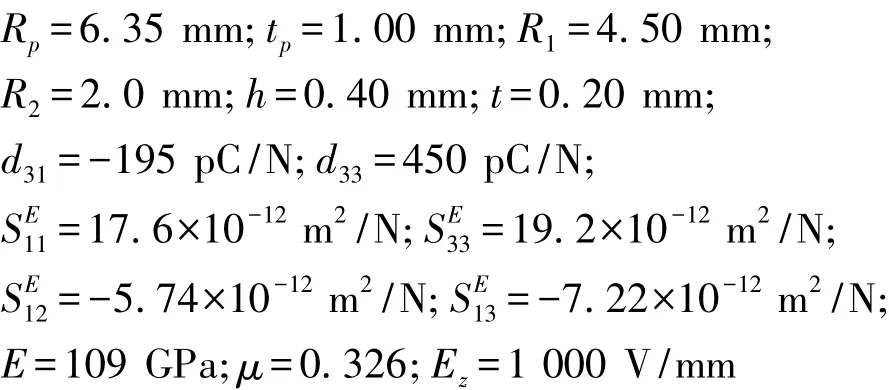
由式(10),代入上述参数,计算得 Δh=1.44×10-5m,再由式(12)计算出de33为14.4 nm/V。对样机采用干涉法测量其de33值[12],结果为 14.4±0.3 nm/V,二者一致。因此,式(11)可以客观描述Cymbal换能器的电压-位移特性本质。
6 Cymbal换能器电压-位移特性函数分析
Cymbal换能器批量加工时性能一致性控制一直是比较棘手的问题。通过分析Cymbal换能器参数对其电压-位移特性函数影响规律,从而确定关键参数误差对其电压-位移特性性能的影响范围区间。这些结论对Cymbal换能器的参数优化设计、大批量生产工艺优化、性能指标一致性控制等方面具有指导意义。
6.1 等效压电常数的稳定性分析
其他条件不变,无负载情况下,Cymbal换能器两端电压从-10 kV到10 kV变化,由精确式(10)和近似式(11)间接计算出来的等效压电常数变化曲线如图3所示。
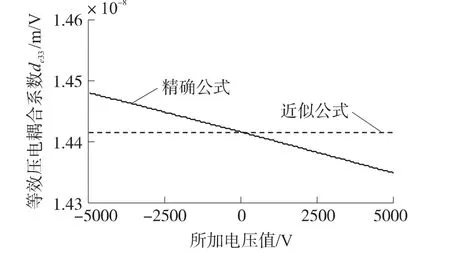
图3 电压-等效压电常数变化曲线
由图3可得结论1:严格意义上讲等效压电常数并非一固定常数,与所加电压有一定关系。电压幅值5 kV范围内波动率在0.5%以内,此时近似公式计算结果可信。
6.2 金属帽材料厚度和内腔高度对等效压电常数的影响
其他条件不变,不同Cymbal换能器金属端帽材料厚度时,内腔高度从0~2 mm变化,得到的等效压电常数曲线簇见图4。
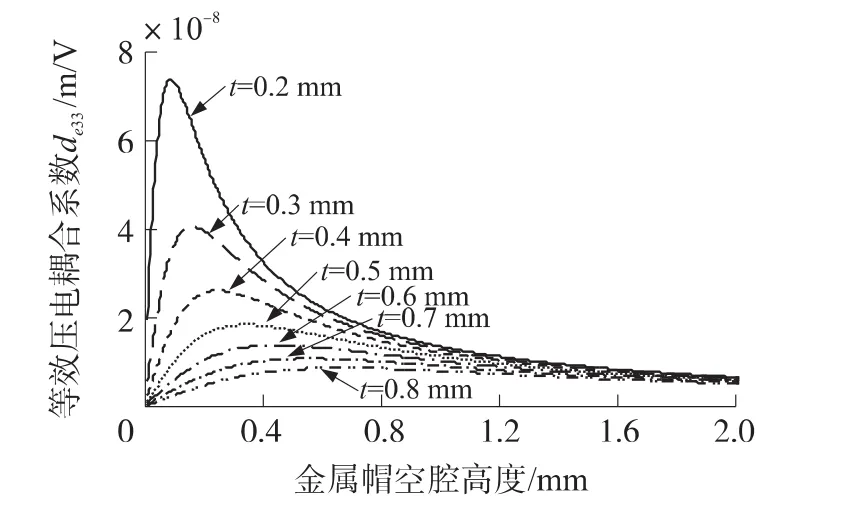
图4 不同材料厚度时内腔高度-等效压电常数曲线
由图4可得结论2:当金属帽材料厚度t确定时,理论上存在一个h,能够使等效压电常数de33的值达到极大值;其他条件不变,厚度t增加时,等效压电常数de33值减小,t值越大,减小趋势越小。
6.3 金属弹性模量对等效压电常数的影响
其他条件不变,金属弹性模量E逐渐变大时得到的等效压电常数变化曲线如图5所示。
由图5可得结论3:当Cymbal换能器结构参数确定条件下,金属弹性模量E增加将会使等效压电常数de33减小,但减小幅值不大。当E增加10倍时,de33仅减小35%。(E=100 GPa 时,de33=1.7×10-8m/V,E=1 000 GPa,de33=1.1×10-8m/V,de33减小 35%)。因此,同一条件下,更改金属材料对等效压电常数的影响有限。
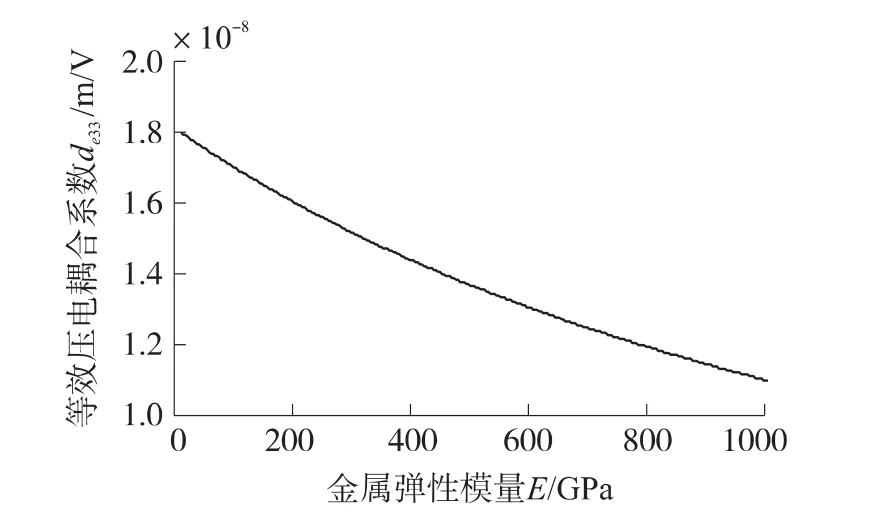
图5 金属弹性模量-等效压电常数变化曲线
6.4 Cymbal金属帽内腔椎顶半径对等效压电常数的影响
其他条件不变,金属帽内腔椎顶半径R2逐渐变大时得到的等效压电常数变化曲线如图6所示。由图6可得结论4:其他条件不变时,Cymbal金属帽内腔椎顶半径R2对等效压电常数de33影响较大,随着R2的增加,de33值成线形急剧下降。
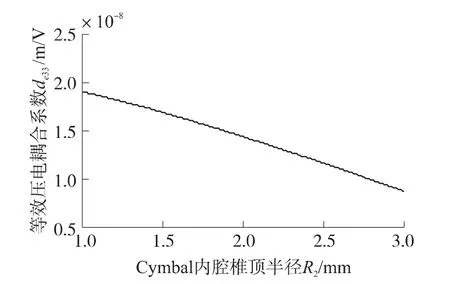
图6 内腔椎顶半径-等效压电常数变化曲线
7 小结
本文通过建立Cymbal型压电换能器电压-位移函数关系模型,并得出了Cymbal换能器几个关键参数对等效压电常数影响规律。这些规律对Cymbal换能器的优化设计、大批量生产工艺优化、性能指标一致性控制等方面具有指导意义。
[1]李邓化,居伟骏,贾美娟,等.新型压电复合换能器及其应用[M].北京:科学出版社,2007:85-92.
[2]Ochoa P,de Frutos J,Femandez J F.Electromechanical Characterization of Cymbal Piezocomposites[J].Smart Materials and Structures,2009,18:1-5.
[3]栾桂冬, , ,等.压电换能器和压电换能器阵[M].北京:北京大学出版社,2005:121-126.
[4]李邓化, , ,等.复合型钹式执行器的高位移性能研究[J].传感技术学报,1999(3):214-217.
[5]邢志波,孙成亮,刘光聪,等.Cymbal换能器试验研究[J].压电与声光,2007,29(3):273-275.
[6]马永成,李邓化,王丽娜.基于ANSYS的Cymbal换能器等效压电常数分析[J].仪器仪表学报,2006,27(6):1313-1315.
[7]崔艳梅,刘向锋,高志.大位移压电陶瓷驱动器的有限元分析[J].传感技术学报,2007,20(10):2239-2242.
[8]吴石林,张玘,黄芝平,等.Spherical-Cymbal换能器位移特性有限元分析[J].传感技术学报,2009,22(1):131-136.
[9]袁旦,李芳,郑方赐.基于非线性有限元法的膜片弹簧特性曲线计算[J].浙江工业大学学报,2009,37(3):350-354.
[10]林成之.圆柱体受均布径向压力作用时的应力分析[J].力学与实践,1988,2:52-53.
[11]潘仲明,刘波.Cymbal型压电复合换能器的数学模型[J].中国机械工程,2006,17(3):283-286.
[12]黄慧明,欧阳俊,国世上.干涉法测量Cymbal换能器的等效压电常量[J].物理实验,2010,30(11):5-7,11.
