一种光纤光栅振动与温度同时区分测量的解调方法

丁 锋，王粉艳，王云建，毕丽华，姚晓静，谭 军

(1.中石化中原油田石油化工总厂仪表车间，河南濮阳 457061；2.濮阳市中远石油技术有限公司，河南 濮阳 457061；3.中石化中原石油勘探局工程建设总公司电气工程处，河南濮阳 457061)

微振动是工程应用中普遍存在的一种现象，如工程机械、旋转机械、海洋石油平台、建筑结构、航空航天器等，这些动力结构不可避免地会出现振动，影响其使用寿命，如果振动剧烈，还会导致构件的破裂。实际应用中往往在振动的同时还会受到温度等其他因素的影响。由于各种因素的相互影响、交叉敏感，多参量的测量技术显得尤为重要。光纤布拉格光栅FBG(Fiber Bragg Grating)作为一种新型的光无源传感器件具有其它传感器无可比拟的优点［1－2］。近年来，国内外对光纤光栅的应变、应力和温度等物理量的传感特性进行了多方面的研究。利用FBG传感器的波长编码特性，不仅可以用来检测温度、应变等准静态量，还可以用来检测加速度、微振动等动态量［3～6］。微振动的检测是一个动态解调的过程，而且振幅不大，要求解调系统的响应速度快、灵敏度高，这就对解调系统提出了很高的要求。而目前，研究最多的是温度与应变的同时测量技术，对温度与振动同时测量的报到甚少。

本文结合了边缘滤波机理中以光源和参考光栅做滤波器的优点，研究了一种对振动与温度的同时区分测量的光纤光栅解调方案，并且实验验证了此方案的合理性和正确性。应用放大自发辐射光源在1 530 nm附近有一段线性区，利用其作边缘滤波器实现了光纤光栅传感解调，并用匹配光栅分离温度对振动的影响。所建立的系统解调相应速度快，符合振动测量的基本要求，且适合在强磁场或强腐蚀性等环镜下对桥梁、水坝、船舰、火车、油田、油罐等的实时监测，以保证其安全、可靠。实现了用单一传感器进行多参量的测量，系统具有易于操控、成本低等特点。

1 基本原理

1.1 边缘滤波解调原理

图1为基于边缘滤波器的线性解调原理示意图，图中的斜线是边缘滤波器的传递函数曲线。光功率的变化量与波长的漂移量成线性关系，即

式中，k、b为边缘滤波器的斜率和截距，都可通过实验测定，且为常数。

当传感光栅受到温度，应变等外界量影响时，光栅的布拉格波长将会漂移。假如从λ1漂移到λ2，光强也将随之由I1变化到I2，通过光电探测器将光强转换为相应的电压，即可求得布拉格波长的变化量。

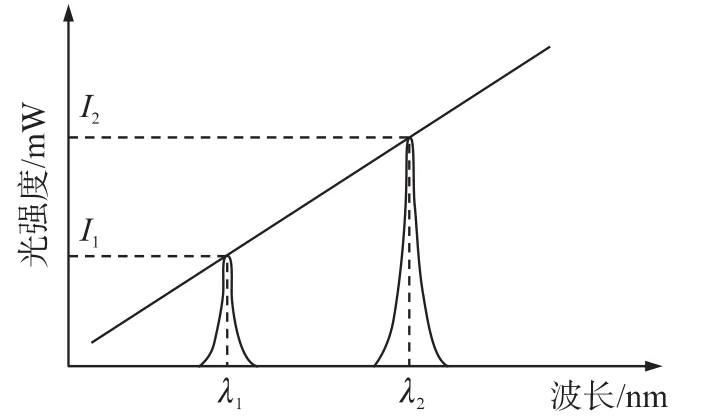
图1 边缘滤波线性解调原理

1.2 振动与温度同时测量原理

如图2示，由放大自发辐射光源ASE(Amplified Spontaneous Emission)发出的光经2/2耦合器分为两束，一束(从3口出来)作为参考信号由光电二极管(PIN3)接收，另一束(由2口出来)入射到传感光纤光栅。当把传感光栅置于振动物体上且周围环境温度发生变化时，传感光栅所反射的中心波长变化既有振动信息又有温度信息。该反射信号经过该耦合器从其4口出来，入射到第二个2/2耦合器的5口，然后又分成两束，一束(从6口出来)由光电二极管(PIN2)接收，用来测量温度，另一束通过7口入射到匹配光栅上，匹配光栅和传感光栅的参数相同，用以消除温度变化对振动的影响，这样从匹配光栅反射回的信号只包括振动信息，并通过第二个3 dB耦合器的8口出来后由光电二极管(PIN1)接收，这样振动和温度信号就被分离出来。由于温度变化比较缓慢，可看作静态信号所以通过低通滤波电路就可以解调出来，而振动信号属于动态信号，我们通过高通滤波电路解调，这样就达到振动和温度同时测量的目的。

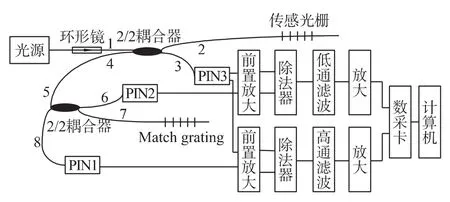
图2 振动和温度同时测量原理图

设传感光栅(FBG1)的中心波长为λB1，半峰全宽为ΔλB1，峰值反射率为R1，匹配光栅(FBG2)的中心波长为λB2，半峰全宽为ΔλB2，峰值反射率为R2。为了解析理论的方便，我们认为经过光栅反射回来的光谱波形是以中心波长为中心的高斯函数［7－8］，因此两光栅的反射光谱函数表达式为

经匹配光栅反射回来的光功率为两个光栅反射的高斯谱的卷积，交叉面积的大小决定光功率的大小，即

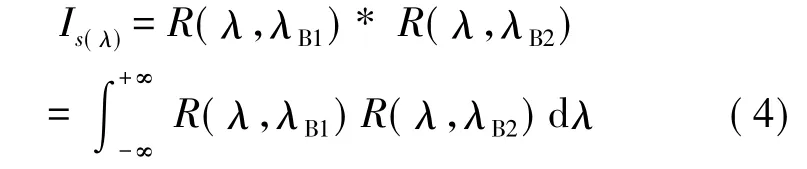
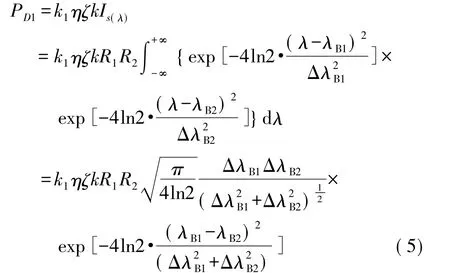
其中，k1为PIN1的响应度，η为光电转换的放大倍数，k为边缘滤波器的斜率，ζ为耦合器分光比的变化及光纤的弯曲和插入损耗等因素造成的总衰减。

当匹配光栅(FBG2)的参数与传感光栅(FBG1)的参数完全相同时，设 λB1=λB2=λB，R1=R2=R，ΔλB1=ΔλB2=ΔλB，则上式变为

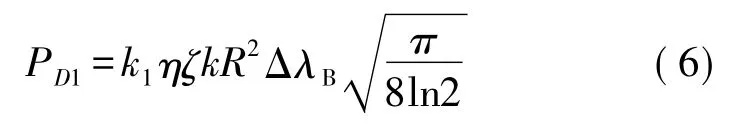
这也是PIN1所能接收到的最大光功率。

然而传感光栅既受温度的调制也受振动的调制，而匹配光栅只受温度的调制。假设环境温度变化引起的光栅布拉格波长漂移量为ΔλT，振动变化引起的光栅布拉格波长漂移量为Δλε。由于实际中没有完全相同的光纤布拉格光栅，传感光栅和匹配光栅的峰值反射率和半峰全宽可以相同，但布拉格波长会有差异，即λB1≠λB2，把这些参量代入式(5)并整理，可得

从式(7)可见，通过匹配光栅可以将温度的变化量消除，从而也证明了采用匹配光栅消除温度对振动的影响是正确的。

当扰动为周期性的正弦信号时，即y=Asinωt，则引起的传感光栅波长变化为Δλ=λBsinωt，则光电探测器接收到的光信号功率为

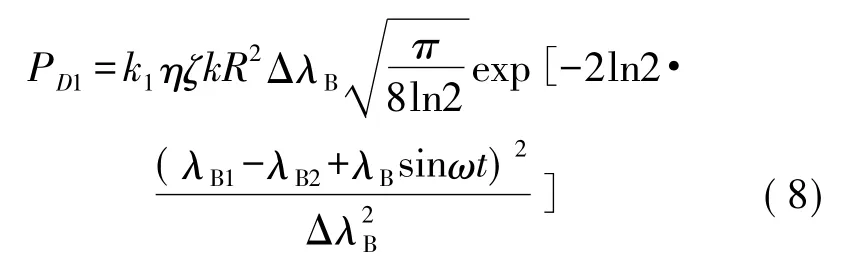
温度变化对Bragg波长的影响是由热膨胀效应和热光效应引起的，由文献［11］知，温度对光纤光栅波长漂移的总影响为

式中，α为光纤材料的膨胀系数，ξ为热光系数。对于石英光纤而言，α 典型值为 5.5×10－7℃，ξ典型值为 6.67×10－6℃－1，温度变化引起的光纤光栅波长漂移主要取决于热光效应，它占热漂移量的95%左右。以典型光栅取布拉格波长为1 550 nm，半峰全宽为0.2 nm，可探测的温度范围约为0～18℃。为避免双值问题而只取用传感光栅反射谱的单边。

2 实验验证及结果分析

应用特制的光源，输出光谱如图3所示。可以看出光源在1 532 nm两边均有一段类线性的部分，其输出的光功率密度随波长变化而线性变化。我们对光源光谱的上升沿1 525.44～1 528.48 nm进行了线性拟合，拟合曲线如图4示。

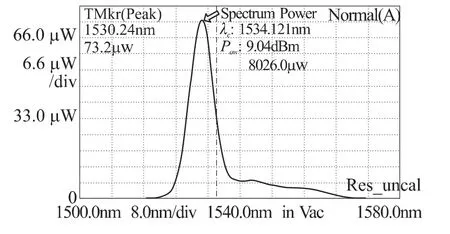
图3 超荧光光源谱密度图

图4 光源部分光谱拟合曲线

上升沿拟合曲线方程为:y=0.013 5x－20.524，线性拟合度R2=0.999 4，光强随波长变化的灵敏度k=0.013 5 mW/nm。

实验采用图2所示的装置图。传感光栅采用的布拉格波长为1 525.912 nm，3 dB 带宽为0.38 nm，峰值反射率为88.78%，粘贴之后的布拉格波长为1 526.78 nm；参 考 光 栅 的 中 心 波 长为1 527.16 nm，半峰全宽为0.38 nm，峰值反射率为88.81%。2个耦合器的分光比均为50/50，放大模块的放大倍数约为106V/A。3个光电探测器均为近红外的高速光电二极管，光谱响应范围900 nm～1 700 nm，其响应度为0.9 A/W。经测量系统建立后的总衰减 ζ=0.062 5。

2.1 对温度的测量实验

对系统进行静态测量，首先是对温度的变化进行测量。将传感光栅放在保温箱中，调节温度的变化，对18℃ ～36℃的温度变化范围进行了测量，为了保证实验的准确性，每次测量的时间间隔为10 min，最终得到光纤光栅的温度响应曲线如图5所示。拟合曲线的方程为:y=0.012 7T+1 526.9，线性拟合度R2=0.999 2。

由图5可以看出，光纤Bragg光栅的温度曲线有很好的线性响应灵敏度。用直线拟合法得到传感光纤光栅的温度灵敏度系数约为0.012 7 nm/℃。在实际的应用中，我们可以将传感光栅换用传感器中心波长在1 527 nm的光纤光栅温度传感器，从而同时测量变化的环境温度，且可测量的温度范围大约为237℃。

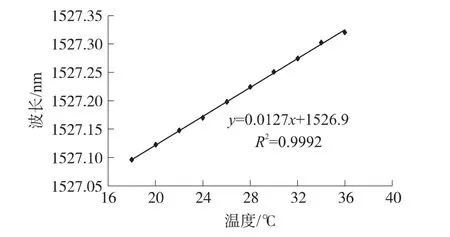
图5 温度测试拟合曲线

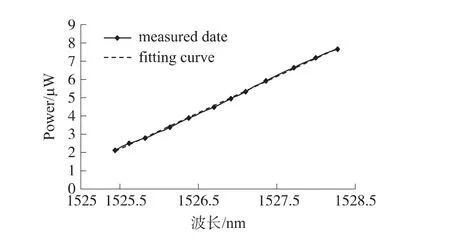
图6 反射峰值功率与波长的拟合曲线

2.2 对振动的测量实验

静态测量时，施加不同的应力来改变悬臂梁结构振动传感器的挠度使悬臂梁弯曲，从而光纤光栅布拉格波长产生蓝移或红移，进而改变了光强和波长。在光谱仪中观测波长的漂移值和反射峰值功率并记录，并对测得的数据进行了拟合分析，拟合曲线如图 6所示。其拟合曲线方程为:y=1.984x+3 024.3，线性拟合度R2=0.999 3。由线性拟合度可以看出，与光源的拟合度之间有偏差，主要的误差来源于随机误差。由式(7)计算得，解调系统的静态波长灵敏度为1 785.6 mV/nm。经测量分析系统可分辨的最小稳定电压为1 mV，故波长的分辨率达到了0.56 pm，由 ΔλB=0.78λB·ε 可得，对应的应变分辨力为0.47 με。电压与温度的灵敏度为22.7 mV/℃，故温度的分辨率达到了0.044℃。

动态测量时，用北京艾普瑞特科技发展有限公司的小型精密振动台(型号WS－Z30－40，工作频率0.5 Hz～3 500 Hz，最大位移±5 mm，最大加速度±10gn)作模拟振源，提供单一频率的正弦信号作微振动信号，把悬臂梁传感器固定在振动台台面上，实验时认为振动台与梁同振动。我们对10 Hz～148 Hz频率的振动信号进行了测试，用NI公司的USB－6211(16 bit，250 kS/s)型数据采集卡对光电转换输出的电信号采样。信号输出端采用LABVIEW编写显示和处理软件［12］，对采集到的数据进行实时监测和分析。图7给出了10 Hz和110 Hz的时域和对应的频谱图，系统的采样频率为 5 kHz，采样点为10 000个。

从图7中上边的时域谱线图可以看出，检测到的电压信号基本为正弦信号，说明所设计的光纤Bragg光栅振动与温度同时测量的解调方案是可行的。图7中下边给出了各个频率所对应的频域谱线图，可以看出频率均单一、主频强度最大且频率值正好是振动台提供的频率值，说明所建立的解调系统可以真实、可靠的反映出被测信号。

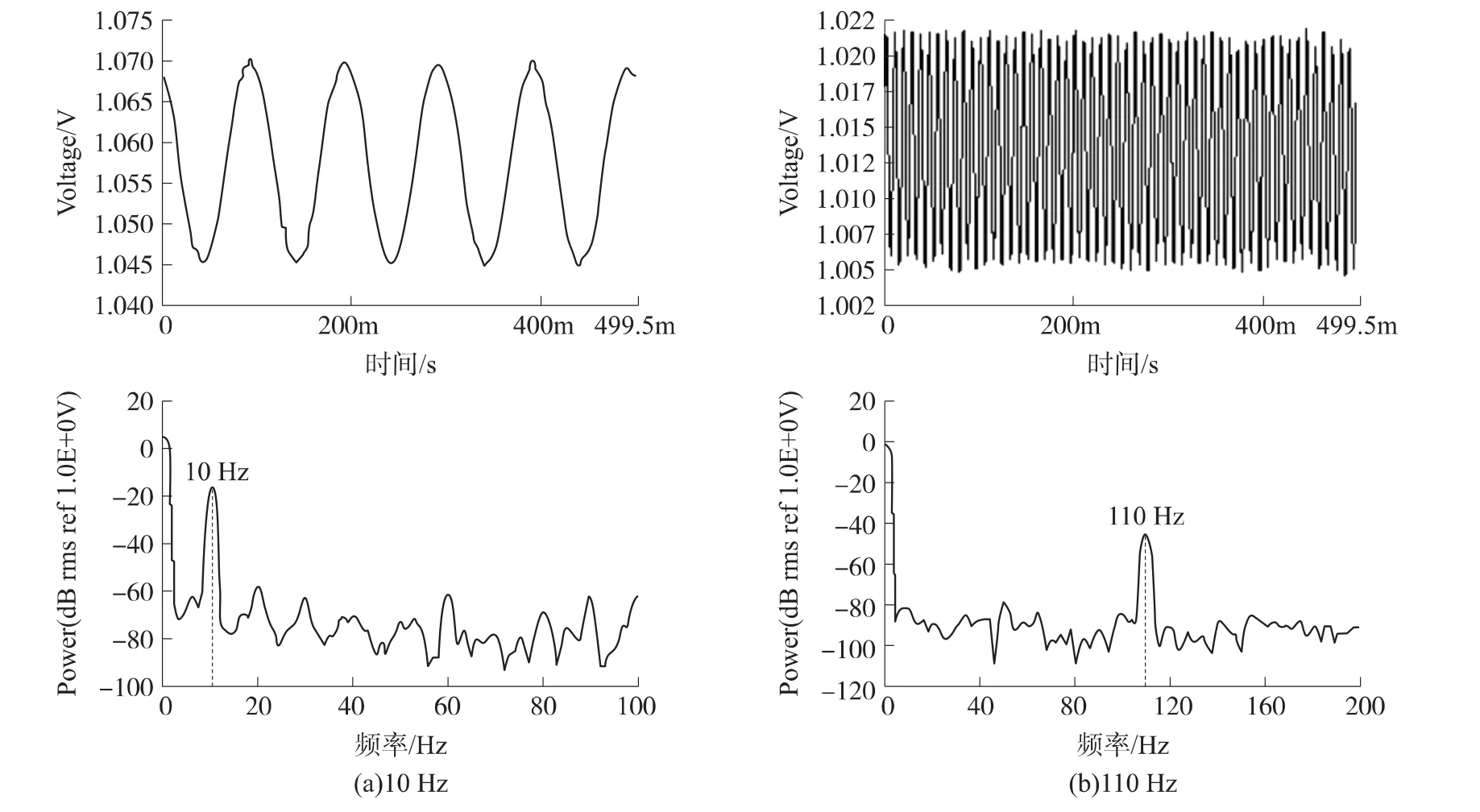
图7 检测光强的电压值随采样时间变化的时域和频谱分布图

3 结论

本文研究了一种振动与温度同时测量的光纤光栅解调方案。对解调方案进行了实验验证，由于振动传感器用的是光栅式，所以对温度的传感灵敏度接近裸光栅的测量灵敏度。而对振动的测量，先对静态进行了测量，通过理论计算，系统的静态波长灵敏度为1 785.6 mV/nm，波长的分辨力达到了0.56 pm，温度的灵敏度为22.7 mV/℃，温度的分辨力达到了0.044℃，并对振动信号也进行了实验验证。实验表明建立的温度与振动同测的解调方案是可行的，具有一定的实用价值，可用于在强磁场或强腐蚀性等环镜下对桥梁、水坝、船舰、火车、油田、油罐等的实时监测。

［1］Morey W W，Meltz G，Glenn W H.Fiber Optic Bragg Grating Sensors［J］.Proc.SPIE，1990，1169:98－107.

［2］Ball D A，Morey W W.Standing-Wave Monomode Erbium Fiber Laser［J］.Photon.Technol.Lett.，1991，3(7):613－615.

［3］乔学光，丁锋，贾振安，等.一种基于ASE光源的边缘滤波解调技术的研究［J］.光电子·激光，2009，20(9):1170－1173.

［4］李志全，朱丹丹，吴飞，等.内含光纤Bragg光栅的微型振动加速度测量探头设计及其理论分析［J］.传感技术学报，2004，17(1):122－124

［5］乔学光，丁锋，贾振安，等.基于光源滤波的高精度光纤光栅地震检波解调系统［J］.光学学报，2010，30(8):2219－2223.

［6］丁锋，李翠翠，乔学光，等.基于边缘滤波解调的光纤光栅低频地震检波器［J］.光电子技术，2010，30(4):236－240.

［7］Limberger H G，Fonjsllaz P Y，Salathe R P.Spectral Characterization of Photoninduced High Efficient Bragg Gratings in Standard TelecommunicationFibers ［J］.Electron.Lett.，1993，29(1):47－49.

［8］Yasukazu Sano，Toshihiko Yoshino.Fast Optical Wavelength Interrogator Employing Arrayed Waveguide Grating for Distributed Fiber Bragg Grating Sensors［J］.Journal of Lightwave Technology，2003，21(1):132－139.

［9］盛秋琴，施可彬，高立模，等.光纤光栅振动传感匹配检测方法的研究［J］.光学学报，2002，22(7):847－851.

［10］励强华，李俊庆，李淳飞.应用平衡双光纤光栅动态解调技术测量应力的研究［J］.光学学报，2003，23(10):1196－1199.

［11］Lam D K，Garside B K.Characterization of Single-Mode Optical Fiber Filters［J］.Applied Optics，1981，20:440－450.

［12］沈小燕，林玉池，付鲁华，等.LabVIEW实现光纤光栅传感解调［J］.传感技术学报，2008，21(1):61－66.