基于高冲击激励的加速度计参数辨识的研究*

胡红波，于 梅

(中国计量科学研究院，北京 100013)

压电加速度计是一种使用非常广泛的微机电装置，在科学研究与工业生产中有着大量的应用。目前，相关的标准都规定了很成熟的确定压电加速度计输入与输出关系的方法［1－2］，但上述加速度计的校准方式都属于基于试验的传递函数估计(即ETFE)，不能用来对激励传感器的非稳态信号进行预测与估计，于是计量领域国际上近几年提出了所谓的动态计量的概念［3－5］，即对测量装置的动态特性进行校准。

通俗地说，所谓动态计量是确定测量系统的频率响应函数，给出测量系统完整的幅度与相位响应，不再是在时域确定测量系统的误差，仪器仪表等学科领域对于这些内容已经做了较为深入的研究。国内这方面突出的贡献者是北京航空航天大学黄均钦教授，其专著《测试系统动力学》［6］标志这一崭新学科的建立；合肥工业大学徐科军教授撰写的《传感器动态特性的实用研究方法》［7］同样对传感器动态特性研究给出了详尽的指导，参考文献［8－13］是各种方法的典型应用。本文参考本领域国内外最新的动态校准方法［14－16］，根据压电加速度计的结构建立了其状态空间模型，利用最优的随机滤波技术Kalman滤波形式，采用基于Hopkinson杆激光绝对法高冲击校准的数据对模型的参数进行了辨识，通过对模型的验证以及在不同的冲击激励峰值下试验的比较，验证了该方法的有效性。

1 绝对法冲击激励校准系统

本文试验所使用校准系统是依据ISO16063－13“绝对法冲击校准”标准的规定建立的高冲击加速度校准系统。该系统原理是利用碰撞产生的应力波在细长杆中传递并在自由端反射产生高峰值、窄脉宽的冲击加速度波形。需要说明的是，该激励系统产生的冲击加速度波形是一个正弦波的形式，不同于碰撞激励系统产生的半正弦平方或者高斯形状的冲击波形。装置结构简图如图1所示。

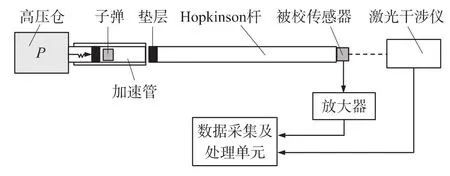
图1 基于Hopkinson杆高gn值冲击校准系统

该高冲击校准系统的工作过程是:高压气体推动子弹在加速管中加速，子弹通过垫层撞击Hopkinson杆的一端，产生的应力波沿杆传递并在安装有被校加速度计的杆的另一端反射从而产生冲击加速度。激光干涉仪测量Hopkinson杆末端的位移，相应的PXI硬件与软件完成数据采集及处理任务。

2 冲击加速度信号的计算

激光干涉仪测量的是冲击过程中的位移信号，其输出是一个相位调制的干涉信号。对激光干涉信号解调可以得到s(t)=s(kT)=s(k)，k=0，1，…，N－1，T为采样间隔。为了得到一个低噪声的位移估计值(k)，我们采用图2的方式来对位移信号进行处理。

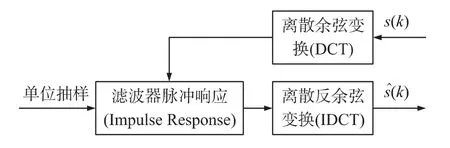
图2 位移信号处理过程

首先对位移信号进行DCT变换，考虑设计一个数字滤波器H(z)，该数字滤波器H(z)的冲击响应具有与位移信号经过DCT变换后的前L项相同。具体该滤波器系数的计算方法可按照Prony算法来确定［17］。本文选择位移信号经过DCT变换后前200个系数，即L=200，滤波器H(z)的分子分母的阶次分别选择45阶，得到的低噪声的位移信号如图3所示。

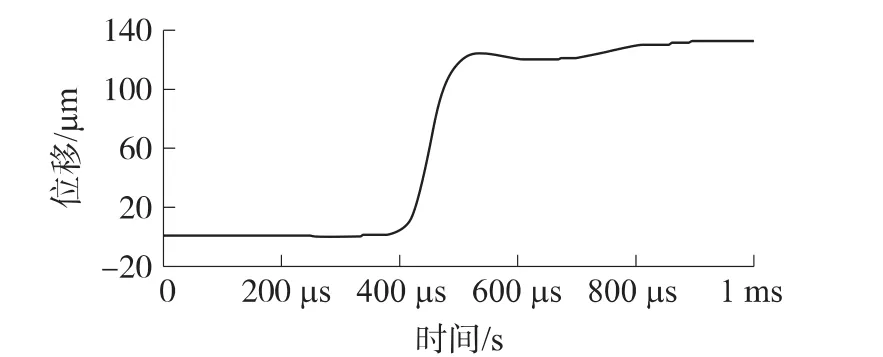
图3 位移信号

对上述位移信号进行微分运算后，得到加速度信号以及传感器输出的电压信号如图4所示。

图4 加速度计输入与输出的信号及其傅里叶谱

由上图可以看出，输入加速度计的冲击加速度峰值约为58 000 m/s2，其频谱范围较宽，覆盖从1 kHz到20 kHz，并且其中间某一些频率成分能量较大，两侧衰减明显。

3 加速度传感器模型的建立

通常我们认为加速度计是一个线性的动态系统，在其线性动态范围内将其等效为一个一自由度的弹簧质量系统［18］，如图5所示。其输入输出微分方程如式(1)所示。

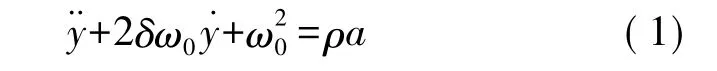
图5 加速度计等效模型

对于式(1)所示的二阶微分方程，引入状态变量x=［x1x2］T，则可以得到一阶状态微分方程为:

加速度传感器输出信号的方程为:

式中，H=［1 0］，w(t)为测量噪声信号。采用零阶保持器对式(2)进行离散化，则可以得到差分方程为:

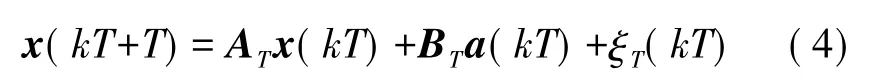
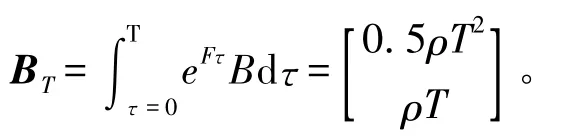
输出方程为:

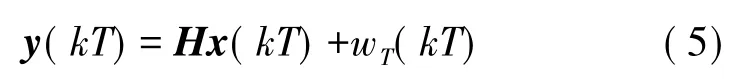
式(4)中，ξT(kT)为零均值高斯分布噪声。对于上面的状态空间模型，给定y(t)，a(t)，设x(kT)，y(kT)的期望为 x*(kT)，y*(kT)，运用 Kalman滤波器形式［17］，可以得到如下的Kalman滤波器方程。

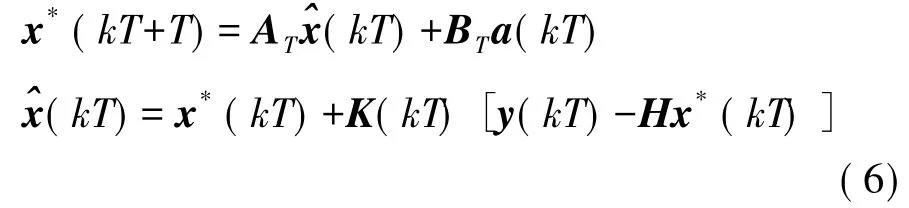
式中K为Kalman系统矩阵。定义预测误差e(t)=y(kT)－Hx*(kT)，则式(6)可以改写为如下形式。

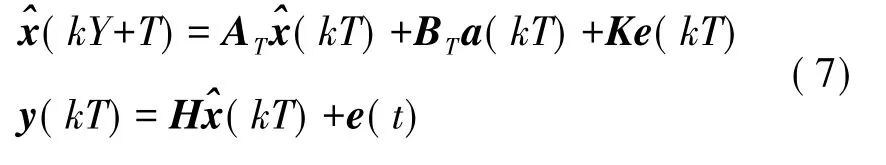
引入一个单位的前向移位因子q，则式(7)可以重新写为如下的形式:

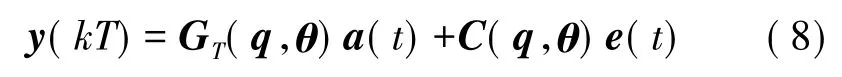
上式中:

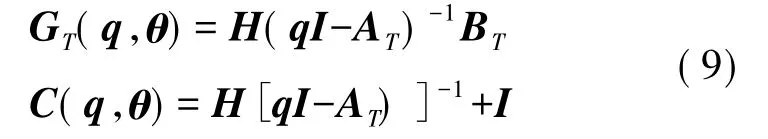
参数θ=［δ ω0ρ］T表示传感器特性参数向量。

4 传感器传递函数参数估计的方法

通过前面建立了加速度传感器的传递函数模型，设得到的加速度计输入输出数据为Z(N)=［y(T)，a(T)，y(2T)，a(2T)，…，y(NT)，a(NT)］，定义任意的一个系数K，计算预测误差e(NT)=y(NT)－Hx*(NT)=e(NT，θ)，最小化下面的范数

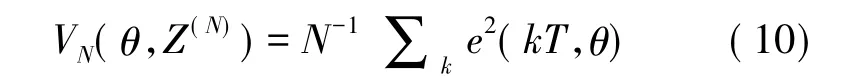
即可以得到参数的估计值=argθmin(VN(θ，Z(N))，将参数估计值代入式(9)即得到了加速度计的传递函数GT(q，θ)。

5 试验结果与模型的验证

利用上述的冲击校准装置，对选定的加速度计进行绝对法冲击校准。激光干涉仪的干涉信号与加速度计输出的电压信号同步采样，采样率100 MHz，利用Matlab软件提供的系统辨识工具箱［19］，计算得到该传感器的动态响应曲线如图6(a)所示.通过得到的多项式系数，可以得到该传感器的谐振频率为350 000 rad/s，即为 56 kHz，阻尼 δ为 0.015。根据传递函数估计(ETFE)方法，图6(b)给出了经过辨识计算得到的传递函数与按照ETFE计算得到的传感器的响应曲线。

从图6(b)我们可以看出，辨识得到的传递函数与按照ETFE计算得到的结果具有良好的一致性。为了进一步对得到的模型参数进行验证，我们比较传感器的实际输出与模型计算得到的输出，结果如图7(a)所示，从该比较图可以看出，模型的输出与传感器的实际输出很吻合。图7(b)显示了在不同的冲击加速度峰值下(gn=9.806 65 m/s2)，通过上述算法计算得到冲击加速度计在0～20 kHz频率范围内，加速度计的幅度谱曲线。

从图7(b)看出，在不同的加速度峰值下，通过上述算法所得到的加速度幅度谱差别都在1%以内，虽然上述实验的冲击加速度峰值范围比较宽，我们可以认为引起上述差别主要的原因是因为噪声而不是加速度计的非线性特性。

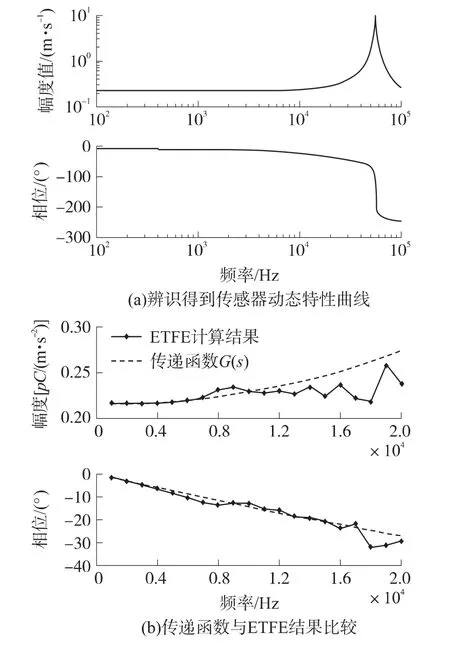
图6 辨识得到传递函数及与ETFE计算得到传感器传递特性比较

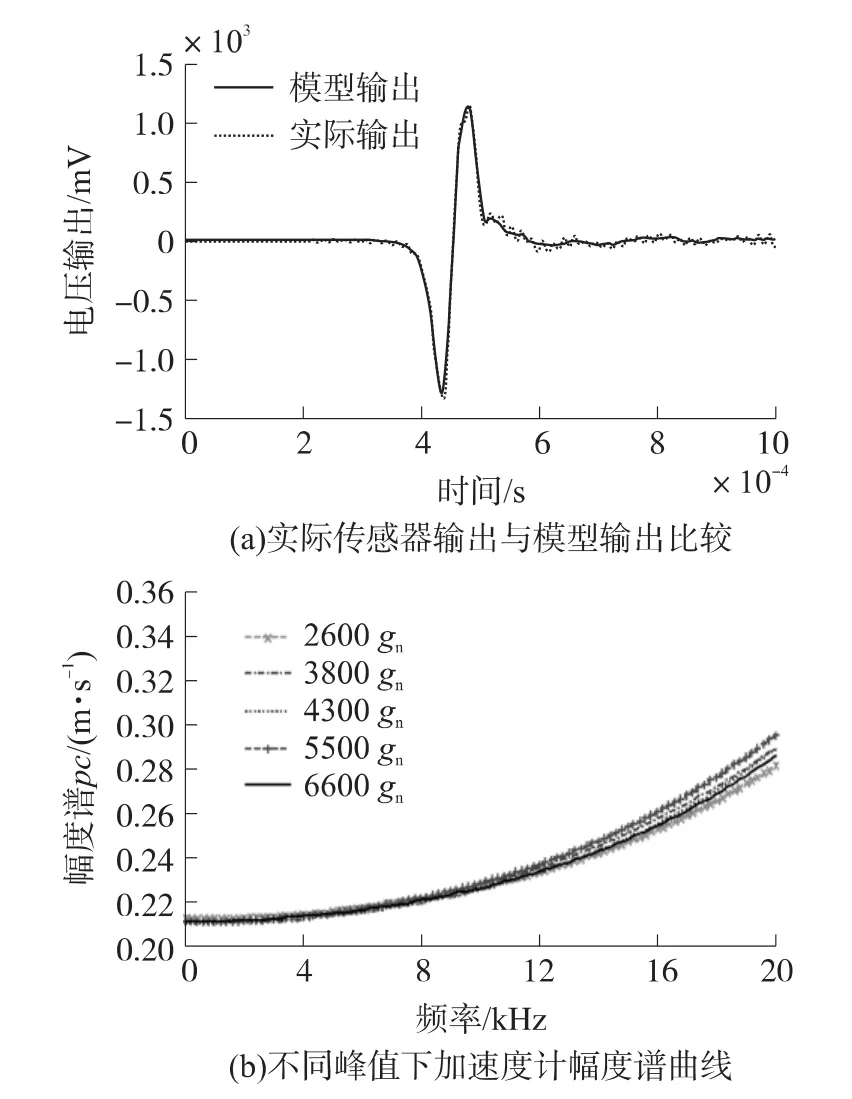
图7 模型输出与不同峰值辨识结果的比较

6 结论

本文根据加速度传感器的物理结构，用状态空间描述了其数学模型，通过激光绝对法冲击校准的数据，对所建立的模型按照相应的算法对其参数进行了辨识。本文所描述的方法在中国计量科学研究院保存的冲击标准装置上进行了测试，试验结果表明该方法能够很好的描述传感器的动态特性。目前本领域国际上正在制定相关的激光绝对法传感器参数辨识的标准，相信该标准的制定对于规范传感器动态校准会起到很大的作用。

［1］ISO 2001 International Standard 16063－13 Methods for the Calibration of Vibration and Shock Transducers—Part 13:Primary Shock Calibration Using Laser Interferometry［S］.(Geneva:International Organization for Standardization)，2001.

［2］ISO 1999 International Standard 16063－11 Methods for the Calibration of Vibration and Shock Transducers—Part 11:Primary Vibration Calibration by Laser Interferometry［S］.(Geneva:International Organization for Standardization)，1999.

［3］Hessling J P.Dynamic Metrology—An Approach to Dynamic Evaluation of Linear Time-Invariant Measurement Systems［J］.Measurement Sci＆ Tech，2008，19:1－7.

［4］Link A，von Martens H J.Accelerometer Identification Using Shock Excitation［J］.Measeurement，2004，35:191－199.

［5］Thomas Bruns，Afred Link，Franko Schmahling，et al.Calibration of Accelerometers Using Parameter Identification—Targeting a Versatile New Standard ［C］//XIX IMERO World Congress，Fundamental and Applied Metrology，September 6－11，Lisbon，Portugal，2009.

［6］黄俊钦.测试系统动力学［M］.北京:国防工业出版社，1996.

［7］徐科军.传感器动态特性的实用研究方法［M］.合肥:中国科学技术大学出版社，1999.

［8］刘清.用多项式预测滤波消噪的传感器动态特性辨识［J］.控制理论与应用，2007，24(4):679－682.

［9］徐科军，陶有军.机器人腕力传感器辨识建模与动态补偿［J］.计量学报，1994，15(2):403－408.

［10］黄俊钦.压力传感器动态数学模型研究［J］.计量学报，1987(3):201－207.

［11］司瑞锋，常炳国，刘君华.基于BP神经网络的传感器特性补偿新算法的研究［J］.仪表技术与传感器，2000(1):11－16.

［12］裴纺霞，王恒辉.基于数据融合的加速度传感器的静态模型辨识［J］.传感技术学报，2005，18(4):894－896.

［13］周红进，许江宁，刘强.扩展卡尔曼滤波应用于加速度计特性估计方法研究［J］.传感技术学报，2008，21(7):1286－1289.

［14］Bruns T，Link A，Elster C.Current Developments in the Field of Shock Calibration［C］//Proc.18th IMEKO World Congress(Rio de Janeiro，Brazil)，2006.

［15］Ueda K，Umeda A.Dynamic Response of Shock Accelerometer Measured Using Davies Bar Technique and Laser Interferometry［C］//Pro.Seventh Int.Cong.on Exp，Mech.Las Vegas USA，8－11 June 1992:1666－1673.

［16］Link A，von Martens H J，Wabinski W.New Method for Absolute Shock Calibration of Accelerometers.Third International Conference on Vibration Measurements by laser Techniques:Advances and Applications［C］//Proc.SPIE，1998，3411:224－235.

［17］张贤达.现代信号处理［M］.北京:清华大学出版社，2002.

［18］樊尚春.传感器技术及应用［M］.北京:北京航空航天大学出版社，2004.

［19］The Mathworks Inc.Matlab with System Identification Toolbox，Signal Processing Toolbox［EB/OL］.