交通流优化速度差模型的非线性分析

周 杰，郝 彦，王朝平

（浙江海洋学院数理与信息学院，浙江舟山 316004）

交通流理论是交通问题的基础研究内容之一，研究的目的是建立能够描述实际交通一般特性的数学模型，揭示各种交通流现象的本质特征．从而为指导交通规划和设计，发展有效的交通控制管理策略和技术提供可靠的理论依据．交通拥堵作为车流交通复杂行为的典型特征之一，多年来已被众多学者通过建立各种模型广泛研究．这些模型主要有跟驰模型、流体力学模型以及元胞自动机模型等等．

跟驰模型是一种典型的微观交通流模型．该模型假设车队在单车道行驶时，不容许超车的情况下，后车跟随前方的车辆行驶，因此称为跟驰模型．跟驰模型较其他模型的一个显著特点是易于得到其解析形式的解．在1953年，PIPES[1]建立了经典跟驰模型，该模型成功描述了连续两辆车的运动过程．1995年，BANDO等[2]通过优化速度函数，建立了优化速度模型．该模型描述了在高速路上，高密度条件下车辆跟驰行为．在众多车辆跟驰模型中，优化速度模型首次反映出交通流的转变原理．但是，与实际数据相比较，优化速度模型存在不切实际的加速或减速现象．为了克服以上不足，HELBING和TILCH[3]在优化速度模型基础上，考虑速度差形式，建立广义力学模型．姜锐[4-5]等在考虑正负速度差基础上，建立了全速度差模型．较之优化速度模型与广义力学模型，该模型在理论上更加符合实际交通状况．2011年，彭光含等[6]通过考虑优化速度差，建立了优化速度差模型，研究优化速度差对交通稳定性的作用．文献[6]利用线性稳定理论，推出了优化速度模型的稳定性条件．但是其没有对模型进行非线性分析．本文将考虑在中性稳定区域以及不稳定区域内，该模型的KdV方程和mKdV方程，并用它们的密度波解来刻画交通拥堵．

本文的主要工作是从优化速度差模型出发，得到模型的等价形式．利用约化摄动法，推导出模型的KdV方程和mKdV方程，并得到其孤立波解与扭结－反扭结波解．

1 优化速度差模型的KdV方程

在文献[6]中，彭光含等人提出优化速度差模型，其形式为

其稳定性条件为

其中性稳定性条件为

为方便下文研究，式(1)可改写为

本小节将从粗粒化的尺度考虑长波模式，通过长波展开，利用约化摄动法[7]，研究在中性稳定线附近亚稳定区域内的交通流状况，导出模型的KdV方程及该方程给出的孤立波形式的密度波刻画交通拥堵．

对空间变量n和时间变量t，分别引入慢变量X和T，

其中b是待定常数，0＜ε＜1[8]．令车头间距可表示成

将式(5)和(6)代入(4)式，将ε做泰勒展开至ε6，得到非线性偏微分方程

在中性稳定线附近的不稳定区域内，设

其中as由式(3)给出．令b=V′(h)，消去式(7)中ε的三阶和四阶形式，得到

对式(9)做如下变量代换

得到带高阶小量的标准KdV方程

若忽略高阶小量ε，式(11)就是标准KdV方程，其孤立波解为

其中振幅A的取值将在下面给出．假设Rk(Xk,Tk)=R0(Xk,Tk)+εR1(Xk,Tk)，考虑式(11)中的O(ε)项，可以在孤立波解系中确定式(11)的唯一解．可解性条件为

这里为式(11)中的项．积分后，得到孤立波的振幅为

替换回原有变量，可以得到由孤立波表示的车头间距为

从以上讨论可以得到结论：中性稳定曲线附近，可以得到KdV方程，其孤立波解刻画了交通流的拥挤密度波．

2 优化速度差模型的mKdV方程

本小节考虑临界点附近的交通流状况，借助速度优化函数

的拐点特性，即V″(hc)=0，在中交通流不稳定区域内推导出模型的mKdV方程，其扭结－反扭结波解刻画了交通拥堵密度波．

对空间变量n和时间变量t，分别引入慢变量X和T，X和T采用式(5)的形式.车头间距表示成

将式(5)和(17)代入(4)式，将ε做泰勒展开至ε5，得到非线性偏微分方程

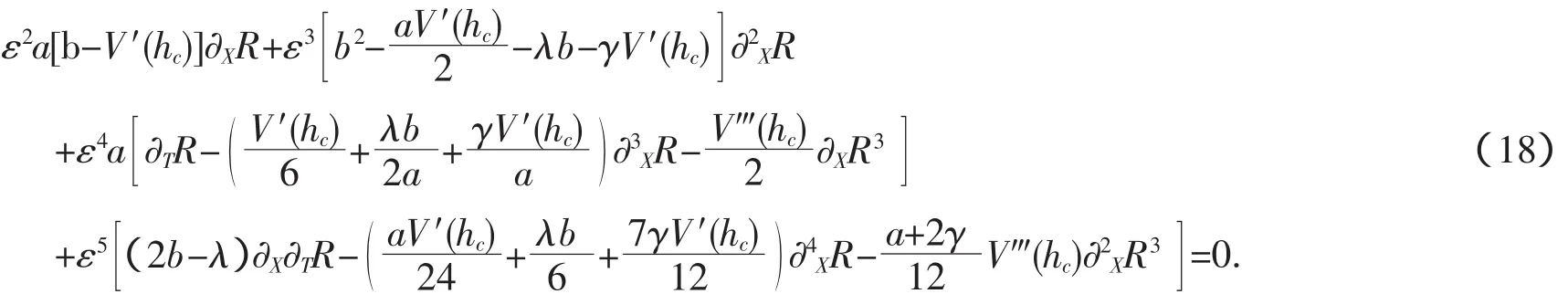
对式(19)做如下变量代换

得到带高阶小量的标准mKdV方程

若忽略高阶小量O(ε)，式(19)就是标准mKdV方程，其扭结－反扭结波解为

由可解性条件，可以得到扭结－反扭结波的传播速度为

替换回原有变量，可以得到mKdV方程的扭结－反扭结波解为

扭结－反扭结波表示的车头间距为

从以上讨论可以得到结论：不稳定区域内临界点附近，可以得到mKdV方程，其扭结－反扭结波解刻画了交通流的拥挤密度波．

[1]PIPES L A.An Operational Analysis of Traffic Dynamics[J].Journal of Applied Physics,1953,24:274.

[2]BANDO M,HASEBE K,NAKAYAMA A,et al.Dynamical model of traffic congestion and numerical simulation[J].Physical Review E,1995,51:1 035-1 042.

[3]HELBING D,TILCH B.Generalized Force Model of Traffic Dynamics[J].Physical Review E,1998,58:133-138.

[4]JIANG R,WU Q S,ZHU Z J.Full velocity difference model for a car-following theory[J].Physical Review E,2001,64：017101-1-4.

[5]JIANG R,WU Q S,ZHU Z J.A new continuum model for traffic flow and numerical tests[J].Transportation Research B,2002,36:405-419.

[6]PENG G H,CAI X H,LIU C Q,et al.Optimal velocity difference model of a car-following theory[J].Physics letters A,2011,375:3 973-3 977.

[7]KOMATSU T,SASA S.Kink soliton characterizing traffic congestion[J].Physical Review E,1995,52:5 574-5 582.

[8]CROSS M C,HOHENBERG P C.Pattern formation outside of equilibrium[J].Review of Modern Physics.1993,65:851-1 112.