先验信息对MCMC方法估计概化理论方差分量变异量的影响

黎光明，张敏强

(1.广州大学 教育学院，广州 510006；2.华南师范大学 心理应用研究中心，广州 510631)

0 引言

MCMC(Markov Chain Monte Carlo)方法源于物理学研究，在统计物理中得到广泛应用已有四十多年的历史[1]。MCMC方法是一种动态的计算机模拟技术，根据贝叶斯（Bayes）推断为中心的多元后验分布，来模拟随机样本的一种方法[2]。上世纪50年代，统计物理学家Metropolis等人引入MCMC，它是一种动态的蒙特卡洛方法[3]。大规模使用MCMC是在上世纪90年代以后，与传统的Monte Carlo方法相比，这种方法可以解决观测分布是复杂的、高维的、非标准化形式的分布[1]。MCMC方法是通过模拟服从某一分布也即平稳分布（Stationary Distribution）(一般是待估参数的联合后验分布)的马尔可夫链，然后根据模拟的马尔可夫链上的样本点对待估参数进行估计。在给定数据的条件下，使用特定的转移核（Markov Kernels）来模拟未知参数的分布，MCMC链就产生在这个迭代过程中。进行MCMC可解决高维积分问题，特别可应用于贝叶斯公式计算，贝叶斯公式[4]可表示如下：

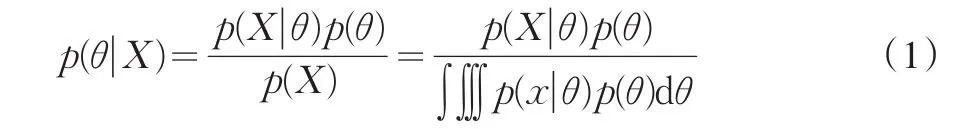
其中，θ=(θ1,θ2,…)，p(θ|X)表示后验条件概率，X为原始分数（本研究原始分数表示模拟生成的数据），θ表示待估的统计量，p(θ)为先验的概率，∫∭ p(x|θ)p(θ)dθ 为需要高维积分的部分。很显然，如果待估参数较少且形式简单，传统的Monte Carlo就可以解决。但是，情况往往并非如此，很多情况下会采用MCMC方法，因为公式（1）高维积分较为困难，就不得不使用其它方法，如MCMC方法。用MCMC方法生成多条链，通过每条链分别构造转移核以使最后能达到平稳分布，然后求取平稳分布上统计量的平均值来估计相应的统计量。不管最初值如何，如果MCMC多条链能够收敛，最后都能得到一个常数值。因为经过高维积分后贝叶斯公式分母变成一个常数（用k表示），那么贝叶斯公式就可表示为：

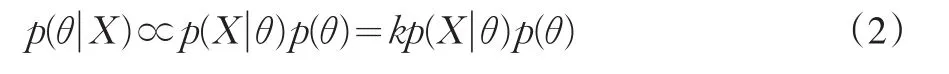
从公式（2）可知，后验概率∝似然函数（likelihood）×先验概率，从此关系可以看出，为了得到后验概率，MCMC方法应该具备三个必要条件：初始值、似然函数和先验概率。如果先验概率分布已知，则MCMC方法称为有先验信息的 MCMC方法（MCMC with informative priors，MCMC inf），否则为无先验信息的MCMC方法（MCMC with non-informative priors，MCMC non-inf）。

Geman和Geman(1984)引入Gibbs算法[5]，现已成为一种标准化的统计计算工具。进行MCMC的Gibbs算法典型软件是WinBUGS软件(Windows operating system version of BUGS:Bayesian Analysis Using Gibbs Sampling)。MCMC方法可以估计模型的各种统计量，如平均数、标准差、百分位数、方差分量等。方差分量（variance component）是指矩阵中的各元素都由若干成分组成，每个分量有各自含义，某一分量占总分量的比例可以用来说明该分量在总方差或协方差中所起的作用。

一般地，仅根据一个样本的统计量来估计总体参数，可能存在偏差。在样本统计量研究中，仅用一个（次）样本平均数来估计总体均值，存在较大的风险，因为样本平均数容易受抽样的影响。例如，某班某次考试平均分为70分，用这个成绩估计这个班的能力水平，必然存在较大风险，这个班下次考试成绩的平均分有可能变为75分。为了降低这种风险，通常的做法是用标准误或置信区间等变异量来估计这个班的实际水平，如70±10或[60,80]。与平均数做法类似，MCMC方法所估计的方差分量，也受到抽样的影响，用某个（次）样本方差分量来估计总体方差分量（参数），存在一定误差。为了降低这种误差带来的风险，需要报告方差分量对应的变异量（如标准误或置信区间），来反映可能存在的变化程度。

概化理论是现代心理与教育测量理论之一[6]。方差分量估计是概化理论的必用技术，是进行概化理论分析的关键。与其它统计量一样，依据概化理论模型所估计出的方差分量受限于抽样，不同的抽样样本，所估计的方差分量可能不一样，这就要求进行方差分量估计时需要对其变异量进行探讨。Tong和Brennan(2006)[7]认为，对方差分量变异量的估计可以使用马尔可夫链蒙特卡洛(MCMC)方法。探讨方差分量变异量具有重要意义，因为报告这些变异量可以在一定程度上说明方差分量测量的可靠性[8,9]。

国内一些学者[10]～[12]对使用MCMC方法估计模型的方差分量进行过研究，另有一些学者在概化理论中使用MCMC方法估计方差分量变异量[13,14]。但鲜有学者关注有无先验信息对MCMC方法估计概化理论方差分量变异量的影响。先验概率是MCMC方法估计各种统计量的必要条件之一，但在现实生活中，我们常常是没有相关先验信息的，这个时候，有先验信息的MCMC方法优势何在，先验信息的有无设定，是否对MCMC方法估计概化理论方差分量变异量有影响等，都需要进行探讨。

1 方法

1.1 数据模拟

运用Monte Carlo数据模拟技术，产生概化理论 p×i（person×item）矩阵数据。数据模拟所使用的软件为R软件，产生模拟数据的过程如下[15]：

（1）定义 p×i数学模型

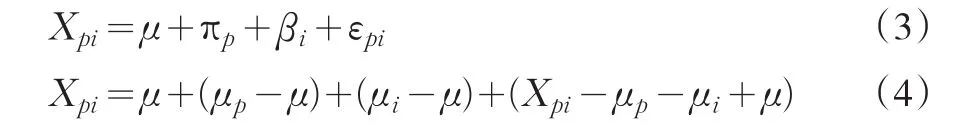
在式（3）和式（4）中，μp-μ=πp表示 p的效应，μi-μ=βi表示i的效应，Xpi-μp-μi+μ=εpi表示 pi的效应。

（2）将公式（4）转换成 Xpi=μ+σpzp+σizi+σpizpi，在参数σp、σi和σpi已知的情况下（μ通常设定为0），调用R软件中的rnorm函数随机生成三个服从正态分布的zp、zi和zpi。

（3）连乘相加获得模拟数据Xpi。假定为参数，其值分别设定为4、16和64。分别构建 p×i设计不同样本容量的三种情况，即100×20、100×40、100×80。生成的模拟数据为矩阵数据（p×i），模拟次数为1000。

1.2 先验信息

依据概化理论模型 Xpi=μ+πp+βi+εpi，为了获得后验概率，参考Mao,Shin和Brennan（2005）的做法[16]，定义似然函数如下：

通过式（6）～（8）设定模型的先验分布，根据共轭分布性质，方差分量对应的分布为逆τ分布，且τ=1/σ2。为定义无先验信息的分布，σ常取0.001，那么τ=106，即认为τ为无穷大。如果为有先验信息的分布，则依具体的先验 值 而 定 ，本 研 究 设 定 p～ τ(2,4) ，i～ τ(2,16) ，pi～τ(2,64)，初始值均为0.001。

1.3 比较标准

设定两种比较标准[14]：一是方差分量标准误估计的比较标准，为“偏差”（bias），计算方法是 bias=(θ^i-θ)，θ^i表示统计量的估计值，θ为参数，偏差的绝对值（称为“绝对偏差”）越大，表明估计值与参数的差异越大，结果越不可靠；二是方差分量置信区间估计的比较标准，为“80%置信区间包含率”，包含率越接近0.80，表明结果越可靠。

1.4 分析工具

R软件、WinBUGS软件、R2WinBUGS软件包和Coda软件包。借助这些软件或软件包，自编完成研究程序。MCMC方法对方差分量及其变异量的估计是通过自编的R程序触发WinBUGS软件“间接”地实现。这个过程要求R软件先调用R2WinBUGS和Coda两个软件包，R2Win-BUGS软件包的作用在于成为R软件和WinBUGS软件的“桥梁”，Coda软件包的作用在于输出WinBUGS软件生成的MCMC结果，如10%和90%两分位点对应的方差分量。

2 结果

2.1 MCMC方法估计的方差分量及其标准误

利用编制的程序估计三种不同样本容量数据的方差分量及其标准误，所得结果如表1所示。

在表1中，np表示人的样本容量，ni表示题目的样本容量，parameters表示参数，vc.p、vc.i和vc.pi分别表示人的方差分量、题目的方差分量以及人与题目交互（包括残差）的方差分量，SE(vc.p)、SE(vc.i)和SE(vc.pi)分别表示人的方差分量标准误、题目的方差分量标准误、人与题目交互（包括残差）的方差分量标准误。MCMC inf和MCMC non-inf分别表示有先验信息的MCMC方法和无先验信息的MCMC方法。

MCMC inf和MCMC non-inf对应两行数据，上一行表示估计的方差分量及其标准误，下一行表示估计的方差分量及其标准误与真值（参数）的偏差，即bias。

表1 方差分量及标准误

2.2 MCMC方法估计的方差分量置信区间包含率

利用编制的程序估计三种不同样本容量数据的方差分量置信区间包含率，所得结果如表2所示。

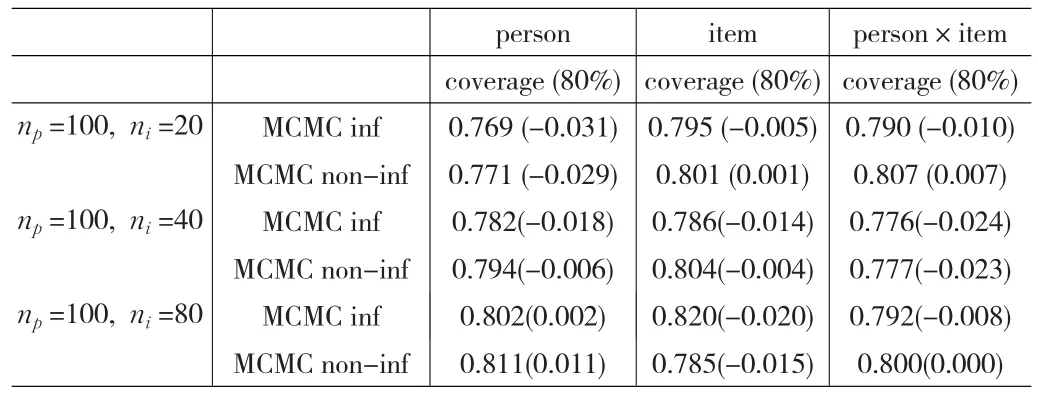
表2 MCMC方法不同样本容量下估计的方差分量置信区间包含率

在表2中，np表示人的样本容量，ni表示题目的样本容量，coverage（80%）表示“80%置信区间包含率”。计算80%置信区间包含率的方法是：通过判断参数是否落入10%到90%两分位点对应的方差分量之间，如果某次成功，则包含次数加1，最后计算落入的总次数，并除以1000，即为最后的包含率。MCMC inf和MCMC non-inf分别表示有先验信息的MCMC方法和无先验信息的MCMC方法。

在表2中，括号中的数值表示估计的方差分量置信区间包含率与0.800（参数）的差值。

3 分析与讨论

3.1 MCMC方法估计的方差分量标准误偏差分析

从表1可以看出，p的样本容量固定为100，i的样本容量逐渐增大（20、40、80）。对于方差分量标准误参数，其值随着i的样本容量增大而趋于减小。例如，i的样本容量为20、40、80时，三个方差分量标准误参数分别为1.0287、0.7968、0.6824，这些值逐渐减小。MCMC inf和MCMC non-inf估计的方差分量标准误随着i的样本容量增大也趋于减小，例如，i的样本容量为20、40、80时，MCMC non-inf估计p的方差分量标准误分别为1.0443、0.8369、0.7149，这些值逐渐减小。方差分量标准误随着i的样本容量增大而趋于减小，符合标准误与样本容量之间的关系。

进一步分析表1可以看出，MCMC两种方法估计的方差分量标准误偏差主要表现在（i题目）上。例如，当np=100，ni=20时，MCMC inf估计的SE(vc.p)、SE(vc.i)、SE(vc.pi)的偏差分别-0.0340、0.0487、-0.0181，SE(vc.i)的偏差最大。再如，当np=100，ni=40时，MCMC non-inf估计的 SE(vc.p)、SE(vc.i)、SE(vc.pi)的偏差分别0.0401、0.2378、-0.0110，SE(vc.i)的偏差最大。因此，考察两种MCMC方法估计的题目的方差分量标准误偏差，更为重要。

比较表1中MCMC inf和MCMC non-inf估计的题目的方差分量标准误偏差，发现前者小于后者，表明有先验信息的MCMC方法较无先验信息的MCMC方法对方差分量标准误的估计要精确些。例如，当题目样本容量增大时（20、40、80），MCMC inf估计SE(vc.i)的偏差分别为0.0487、-0.1090、0.0859（已用虚线方框括起），MCMC non-inf估计SE(vc.i)的偏差分别为1.0434、0.2378、0.1059（已用实线方框括起），明显可以看出，MCMC non-inf估计的SE(vc.i)的偏差要大于MCMC inf估计的SE(vc.i)的偏差。

但是，随着i的样本容量增大，MCMC non-inf和MCMC inf估计的题目的方差分量标准误偏差，趋于接近。例如，当np=100，ni=20时，两种方法估计的SE(vc.i)的偏差分别为1.0434和0.0487，偏差差值为0.9947；当 np=100，ni=40时，两种方法估计的SE(vc.i)的偏差分别为0.2378和-0.1090，偏差差值为0.3468；当np=100，ni=80时，两种方法估计的SE(vc.i)的偏差分别为0.1059和0.0859，偏差差值为0.0200。

3.2 MCMC方法估计的方差分量置信区间包含率分析

从表2可知，有先验信息的MCMC方法和无先验信息的MCMC方法随着i的样本容量增大，估计的方差分量置信区间包含率并没有表现出一定的规律性。但是，从两种MCMC方法估计的置信区间包含率看，两种方法都接近于0.800，并且包含率与0.800的差值的绝对值在0.000～0.031之间，差值的绝对值较小。因此，可以认为两种MCMC方法都较好地估计了方差分量的置信区间。

进一步分析表2可以看出，随着i的样本容量增大（20、40、80），无先验信息的MCMC方法并不是在所有方差分量置信区间估计上都优于有先验信息的MCMC方法，例如，当np=100,ni=80时，有先验信息的MCMC方法估计的p的方差分量置信区间包含率为0.802(0.002)（已用方框括起），而无先验信息的MCMC方法为0.811(0.011)，有先验信息的MCMC方法好些。对于估计的方差分量置信区间包含率与0.800的差值，从总体上看，有先验信息的MCMC方法与无先验信息的MCMC方法相距较小，表明两种方法估计方差分量置信区间精确度相当。这就是说，在变化样本容量的条件下，有时无先验信息的MCMC方法估计某些方差分量置信区间的结果好些，有时却是有先验信息的MCMC方法好些。但从总体上看，两种方法精确度相当。

4 结论

（1）在方差分量标准误这个变异量估计上，有先验信息的MCMC方法较无先验信息的MCMC方法要精确些，但随着i的样本容量增大，这种趋势减小。

（2）在方差分量置信区间这个变异量估计上，随着i的样本容量增大，有先验信息的MCMC方法和无先验信息的MCMC方法的精确度相当。

[1]茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社,1998.

[2]王权编译.马尔可夫链蒙特卡洛(MCMC)方法在估计IRT模型参数中的应用[J].考试研究,2006,(4).

[3]Metropolis,N.,Rosenbluth,A.W.,Rosenbluth,M.N.,Teller,A.H.Teller,E.Equations of State Calculations by Fast Computing Machines[J].Journal of Chemical Physics,1953,(21).

[4]魏宗舒.概率论与数理统计教程[M].北京:高等教育出版社,1983.

[5]German,S.,German,D.Stochastic Relaxation,Gibbs Distribution and the Bayesian Restoration of Images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1984,(6).

[6]杨志明,张雷.测评的概化理论及其应用[M].北京:教育科学出版社,2003.

[7]Tong,Y.,Brennan,R.L.Bootstrap Techniques for Estimating in Gener⁃alizability Theory(CASMA Research Report No 15).Iowa City,IA:Center for Advanced Studies in Measurement and Assessment,Uni⁃versity of Iowa[EB/OL].http://www.education.uiowa.edu/casma,2006.

[8]American Educational Research Association.American Psychological Association,National Council on Measurement in Education.Stan⁃dards for Educational and Psychological Testing[Z].Washington,DC,1985.

[9]American Educational Research Association.American Psychological Association,National Council on Measurement in Education.Stan⁃dards for Educational and Psychological Testing(Rev.ed.)[Z].Wash⁃ington,DC,1999.

[10]马跃渊,徐勇勇,奚苗苗,遇苏宁.有缺失数据的生物等效性评价的MCMC方法[J].中国卫生统计,2004,21(4).

[11]马跃渊.医学数据统计分析中MCMC算法的实现与应用[D].第四军医大学硕士论文,2004.

[12]郜艳晖,姜庆五,孟炜,陈启明,赵耐青,沈福民.REML法和MCMC法在数量性状核心家系遗传方差分量模型中的参数估计的比较[J].复旦学报,2003,30(4).

[13]黎光明,张敏强.一项跨分布研究:基于概化理论的方差分量变异量估计[D].北京师范大学首届全国心理学博士学术论坛论文集,2009a.

[14]黎光明,张敏强.基于概化理论的方差分量变异量估计[N].心理学报,2009b,41(9).

[15]Brennan,R.L.Generalizability Theory[M].New York:Springer-Ver⁃lag,2001.

[16]Mao,X.,Shin,D.,Brennan,R.L.Estimating the Variability of Esti⁃mated Variance Components and Related Statistics Using the MC⁃MC Procedure:An Exploratory Study[C].Paper Presented at the An⁃nual Meeting of the National Council on Measurement in Education,Montreal,2005.