钢－泡沫结构冲击性能的建模方法

张金军，王 林，蔡厚平

(1.南通航运职业技术学院，江苏 南通 226010;2.江苏科技大学，江苏 镇江 212003)

0 引言

钢－泡沫结构是由上面板、泡沫及下面板组成，这种结构具有优异的抗冲击性能和抗破损能力，使船舶更安全可靠。同时泡沫粘合到里外2层钢板上，为钢板提供了连续均匀的支撑，提高了钢板的局部抗弯能力。将钢－泡沫结构替换船原有的常规结构，可以有效地吸收和传递外部海浪，减少碰撞及搁浅可能造成的局部冲击和破坏［1－2］。

1 钢－泡沫结构的力学特性［3］

1.1 钢－泡沫结构的基本参数

钢－泡沫结构主要参数如下(见图1):tc为泡沫厚度;t1为上层面板厚度;t2为下层面板厚度;B为泡沫材料宽度;L为泡沫材料长度。

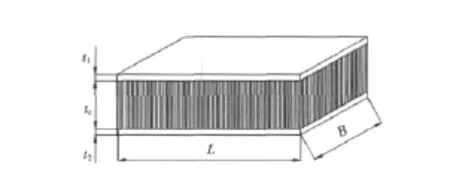
图1 钢－泡沫结构Fig.1 Steel-foam structure

1.2 钢－泡沫结构平衡方程［4］

钢－泡沫结构的上下2层面板的厚度均为t，泡沫厚度为tc。假设材料均为各项同性材料，其平衡方程、应变位移关系和层合板一致，仅有本构方程不同。下面将分别给出各方程。根据经典线性薄板理论，对于如图2所示的矩形板进行面内载荷和侧向载荷分析，如图3和图4所示。

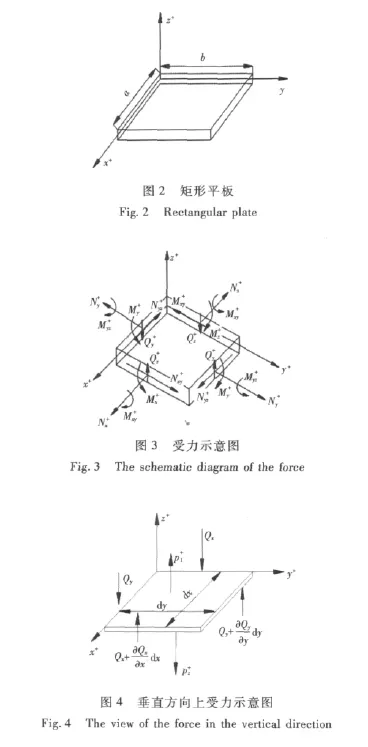
可以推导出如下平衡方程:

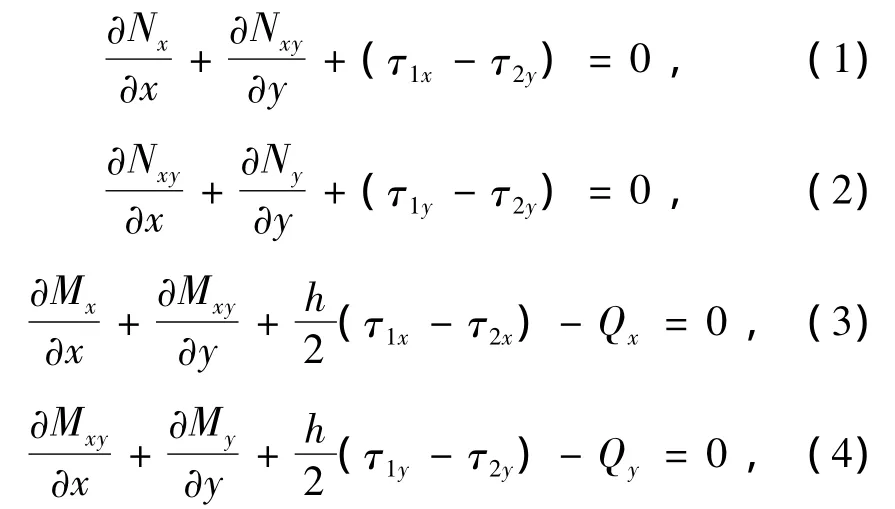
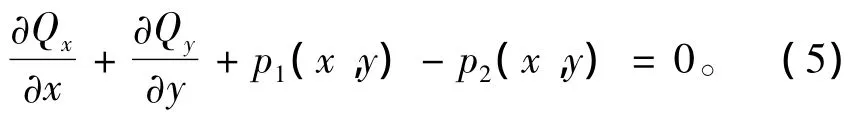
其中，τ1y= σyz(+h/2);τ2y= σyz(－h/2);p1(x，y)= σz(+h/2);p2(x，y)= σz(－ h/2)。

1.3 钢－泡沫结构应变位移关系

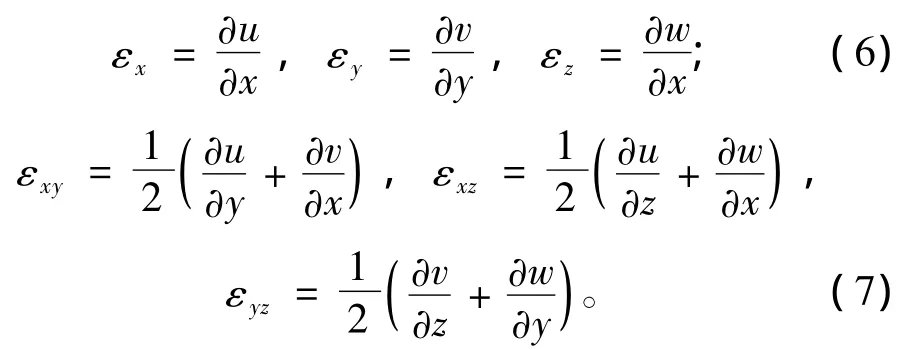
1.4 钢－泡沫结构本构方程

钢－泡沫结构本构方程的推导和层合板实质上是一致的，钢－泡沫结构是3层板结构，而层合板是多层结构如图5所示，可以将钢－泡沫结构的下面板看作是层合板的第1层，泡沫看作是层合板的第2层，上面板看作是层合板的第3层。

图5 层合板结构Fig.5 The structure of laminate

根据经典层合板理论，层合板的本构方程为:

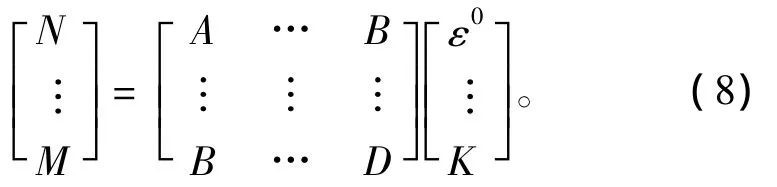
其中，Aij为拉伸刚度系数;Dij为弯曲刚度系数;Bij为耦合刚度系数。

拉伸刚度系数

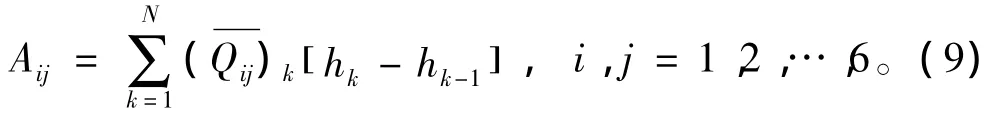
钢－泡沫结构N=3，上式可展开为:

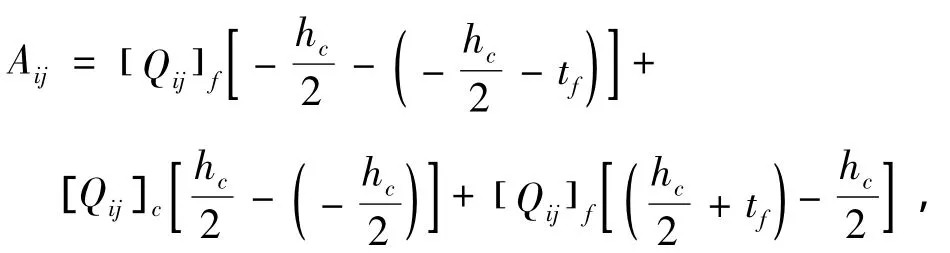
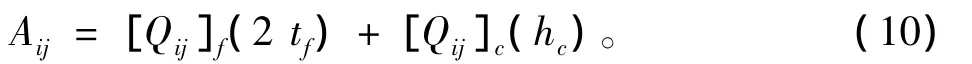
弯曲刚度系数

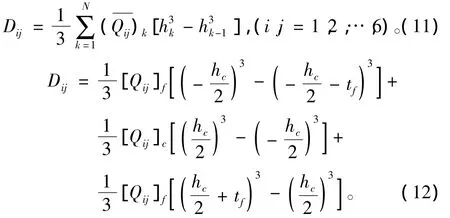
因为泡沫很弱(Ec＜＜Ef)，所以可忽略泡沫对拉伸刚度Aij的贡献;同样，可以将钢－泡沫结构的承弯形式看作工字梁的承弯形式(腹板、泡沫只对高度有贡献)。此外，本文只考虑上下面板等厚(横截面对称)的钢 － 泡沫结构，所以 Bij=0(i，j=l，2，…，6)，并且式(10)和式(11)可化简为:

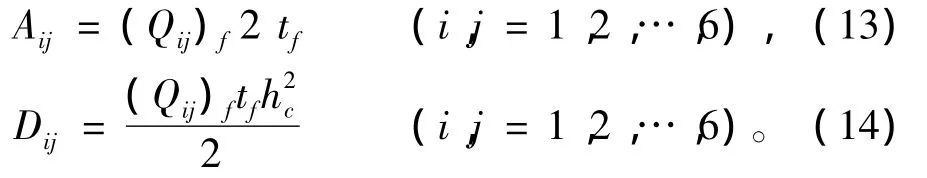
2 钢－泡沫结构冲击性能分析

2.1 冲击结构的选取

1)尺寸选取

选取一长度为2 m，宽度为2 m的矩形钢－泡沫结构，上下面板厚为2 mm，泡沫层厚度为15 mm。撞体为1个半径80 mm的球体。

2)材料选取

上下2层钢材面板:弹性模量210 GPa，泊松比为0.3，密度为7 850 kg/m3，屈服应力为235 MPa，硬化模量为1.18 GPa，最大塑性应变为0.3;

泡沫材料:弹性模量为1.916 GPa，泊松比为0.476，密度为1 200 kg/m3，屈服应力为26 MPa，最大塑性应变为0.5;

球体:球壁厚为10 mm，重量为10 t，其材料为钢材。

3)冲击过程

撞击球距钢－泡沫结构的表面距离为1 mm，同时以5 m/s的速度冲击钢－泡沫结构。

2.2 冲击的有限元模型［5］

考虑到实际结构几何复杂性，在进行碰撞有限元分析时有必要根据研究对象的差异，选用不同的有限元建模方法，以达到高的求解精度以及可以接受的效率。这里主要讨论3种有限元建模方式，将碰撞力的有限元计算结果与经验公式的结果进行对比，从而对后面系统分析钢－泡沫结构的碰撞性能提供一些参考依据。

1)模型1:Laminate模型

采用2D模型，用Laminate模拟钢－泡沫结构(见图6)。

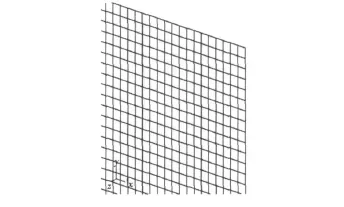
图6 Laminate模型Fig.6 FEM with Laminate

2)模型2:体元加壳元模型

上下面板采用2D壳元模拟，中间泡沫采用实体元模拟(见图7)。

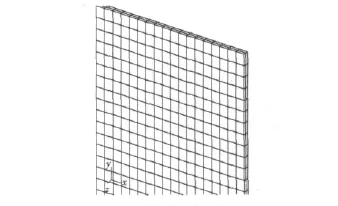
图7 体元加壳元模型Fig.7 The model of solid and shell

3)模型3:体元模型

上下面板和泡沫都采用3D实体元模拟(见图8)。

2.3 材料模拟

1)模型1:泡沫和上下面板都采用 DMATEP(shell)进行模拟。

2)模型2:上下面板采用DMATEP(shell)进行模拟;泡沫采用DYMAT24(solid)进行模拟。

3)模型3:泡沫和上下面板都采用DYMAT24(solid)进行模拟。

2.4 接触算法

选择 Contact——Adaptive master-slave surface，来模拟碰撞过程中球体与钢－泡沫结构的接触。

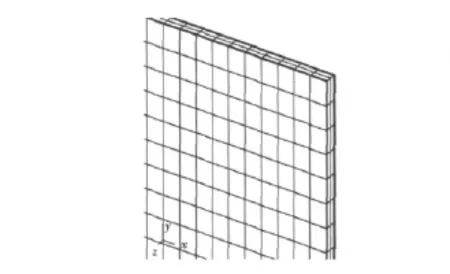
图8 实体元模拟Fig.8 The model of solid

2.5 约束条件

对钢－泡沫材料的四周进行刚性约束。

在 x，y=0，2 m 时，Ux=Uy=Uz=0，Rx=Ry=Rz=0。

2.6 结果分析(侧重于碰撞力分析)

本节主要侧重于对碰撞力分析研究，进而比较不同模型的建立对结构整体碰撞性能的优劣。

1)模型1:Laminate模型

利用动态非线性有限元分析软件MSC.Dytran对该仿真模型进行计算。在整个损伤过程中，计算耗时为10 min 31 s，计算步长取为100步。

图9反映钢－泡沫结构采用Laminate建模后碰撞力的变化曲线。图中显示，碰撞力曲线具有明显的非线性，在t=0.038 s时，碰撞力达到极值，极值为1.99×106N。开始撞击时，由于整个板都会对撞头触及区域起到抵抗作用，致使撞击力明显减小，进而起到减缓作用。随着碰撞的进行，碰撞力逐渐增大。在B处，碰撞力出现第一次卸载代表下层面板的失效。由于钢－泡沫结构的多层作用，在碰撞过程中，板没有整体失效。在C处，经过多次卸载，各层材料达到完全失效。随着碰撞的进行，碰撞力呈现迅速下降的趋势。

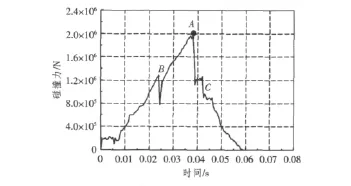
图9 碰撞力与时间关系曲线Fig.9 Curve of collision force-time

2)模型2:体元加壳元模型

利用动态非线性有限元分析软件MSC.Dytran对该仿真模型进行计算。在整个损伤过程中，计算耗时为49 min 41 s，计算步长取为100步。

图10反映了钢－泡沫结构采用壳元加体元建模后碰撞力的变化曲线。图中显示，碰撞力曲线具有明显的非线性，在t=0.04 s左右时，碰撞力达到极值，极值为2.21×106N。结合损伤变形，在t=0.037 5 s时，第1次卸载，主要由于钢－泡沫结构的下层面板失效;当t=0.04 s时，出现第2次明显卸载，因为钢－泡沫结构的上层面板已达到失效状态;当t=0.042 5 s时，中间泡沫层也出现破损，此时各层材料均达到失效。随着碰撞的进行，失效的钢－泡沫结构对撞头的阻碍作用随即下降，此时在C处的碰撞力呈现明显下降的趋势。

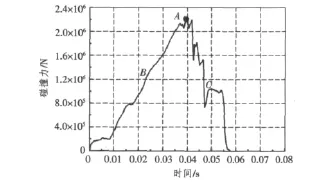
图10 碰撞力与时间关系曲线Fig.10 Curve of collision force-time

3)模型3:体元模型

利用动态非线性有限元分析软件MSC.Dytran对该仿真模型进行计算。在整个损伤过程中，计算耗时为10 h 21 s，计算步长取为100步。

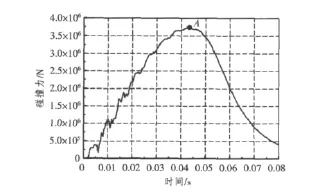
图11 碰撞力与时间关系曲线Fig.11 Curve of collision force-time

图11反映了钢－泡沫结构采用体单元建模后碰撞力的变化曲线。图中显示，碰撞力曲线具有明显的非线性，在t=0.041 5 s时，碰撞力达到极值，极值为3.70×106N。在A处，碰撞力出现最大值，由于夹层材料的多层作用，在碰撞过程中，板趋于整体失效。随着碰撞的继续进行，碰撞力呈现迅速下降的趋势。

2.7 最大碰撞力的经验公式计算比较

1)美国指导规范给出最大碰撞力［6］:

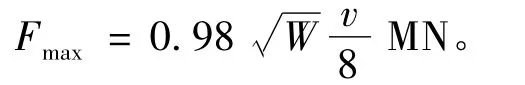
式中:W为船舶载重量(碰撞物的质量)，t;v为撞击速度，m/s。

故，

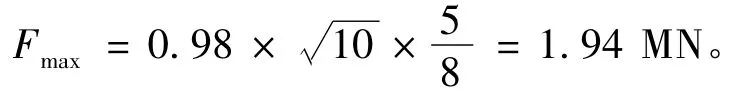
2)AASHTO船桥碰撞设计指南给出的船首正碰撞击计算公式［7］:

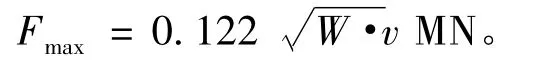
故，

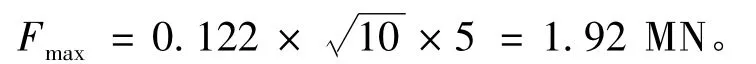
由表1可见，采用Laminate对钢－泡沫结构进行建模计算后最大碰撞力为1.99 MN，与经验公式得出的结果1.94 MN和1.92 MN比较接近。一方面，钢－泡沫结构的模型符合使用铺层方法(Laminate)建模的假定;另一方面，钢－泡沫结构用Laminate计算时间较其他2种方法要短，节省碰撞过程中的计算时间。因此，对钢－泡沫结构进行碰撞研究时所采用的建模方式为铺层方法。

3 结语

本文主要从层合板的理论出发，研究分析钢－泡沫结构的相关力学性能。同时运用有限元软件进行计算、分析和比较，确定较为理想的建模方式。得出以下结论:

1)从经典的层合板理论出发，根据钢－泡沫结构的强度以及受力特点，引出钢－泡沫结构的本构关系。

2)在对钢－泡沫结构的冲击进行数值模拟时，最终得出的最大碰撞力与经验公式进行比较分析，确定采用铺层方法(Laminate)这种建模方式为最佳的数值模拟方式，可对钢－泡沫结构的碰撞性能进行综合研究与分析。

［1］王自力，顾永宁.船舶碰撞研究的现状和趋势［J］.造船技术，2000，(4):9 －14.

［2］祁恩荣，崔维成.船舶碰撞和搁浅研究综述［J］.船舶力学，2001，(4):67 －80.QI En-rong，CUI Wei-cheng.A state-of-the-art review on ship collision and grounding［J］. JournalofShip Mechanics，2001，(4):67 －80.

［3］CASTANIE B，BARRAU J J，JAOUEN J P.Theoretical and experimental analysis of asymmetric sandwich structures［J］.Composite Structures，2002，55:295 －306.

［4］徐胜今，孔宪仁，王本利，等.正交异性蜂窝钢－泡沫结构动、静力学问题的等效分析方法［J］.复合材料学报，2000，17(3):92 －95.XU Sheng-jin，KONG Xian-ren，WANG Ben-li，et al.Mehtod of equivalent analysis for statics and dynamics behavior of orthotropic honeycomb sandwich plates［J］.Acta Materiae Compositae Sinica，2000，17(3):92 －95.

［5］李毅，王生楠.轻质夹层复合结构稳定性及冲击性能分析［D］.西安:西北工业大学，2007.

［6］PEDERSEN P T，ZHANG S.On impact mechanics in ship collisions［M］.Marine Structures，1998.429 －449.

［7］DERUCHER K N.Proposed AASHO standards for the design of bridge protective system［J］.Civil Engineering for Practicing and Design Engineers，1982，1(2):131 －145.