非负矩阵最大特征值的新界值
2012-10-18贾利宁
贾利宁
(天津大学数学系,天津300072)
非负矩阵理论作为一种基本工具,被广泛地应用到数学的各个分支及其他科学领域,非负矩阵最大特征值的估计是非负矩阵理论的核心问题之一.如果其上下界能够表示为以矩阵为元素的易于计算的函数,那么这种估计的价值更高.
由Frobenius界值定理[1]知
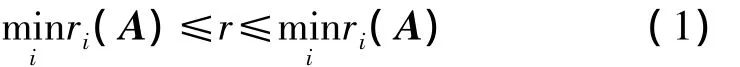
同理对A的列和也有相同的结论.对于有非零行和的非负矩阵,H·Minc在文献[1]中把(1)
式进一步推广为:
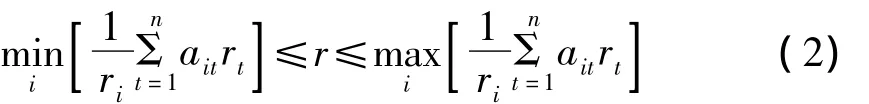
引理1[2]设A=(aij)为n阶非负不可约矩阵,B=(A+1)n-1,其中I为n阶单位阵,则对任何正整数k有

1 界值定理
引理2[1]设 λ是矩阵A的特征值,分别是矩阵AT和A对应于λ的特征向量,则
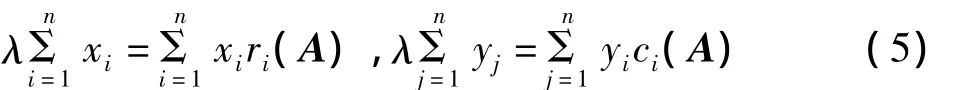
引理3[1]若q1,q2,…,qn是正数,则对任意实数p,p2,…,pn,有
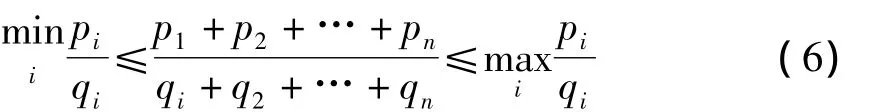
引理4[3]设A是n阶矩阵分别表示矩阵Ak的第i行的行和与第j列的列和,则

其中i,j∈〈n〉,s,k均为非负整数s≤k,且约定A0=I(I为单位矩阵).
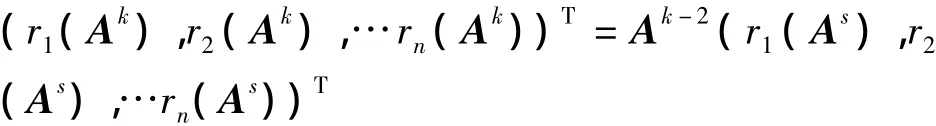
定理1设A=(aij)为n阶非负不可约矩阵,r为A的最大特征值,分别表示矩阵A2k的第i行的行和与第j列的列和,且B=(A- αI)n-1,其中 α=mini{aij}则对任意正整数k(≥1),有
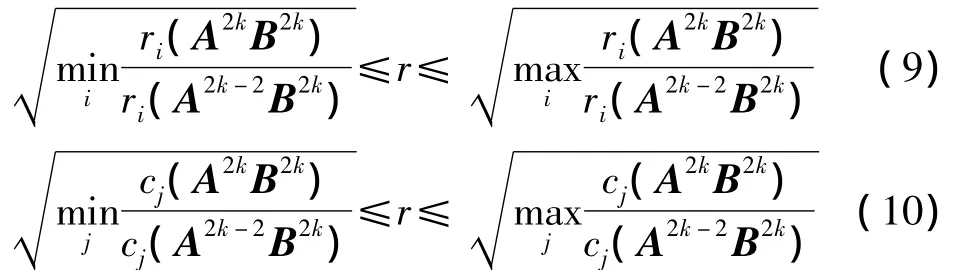
由引理2得
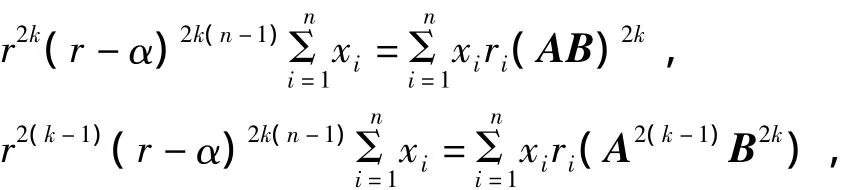
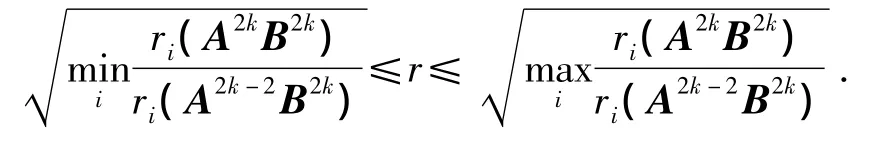
定理2设A=(aij)为n阶非负不可约矩阵,r为A的最大特征值分别表示矩阵A2k的第i行的行和与第i列的列和,且B=(A- αI)n-1,其 中 α=mini{aii}则有与存在,且
证明 设x=(x1,x2,…,xn)T>0,是矩阵A对应于r的特征向量,不妨设.因为B=(A-
αI)n-1,则有AB=BA,从而
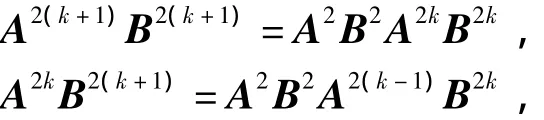
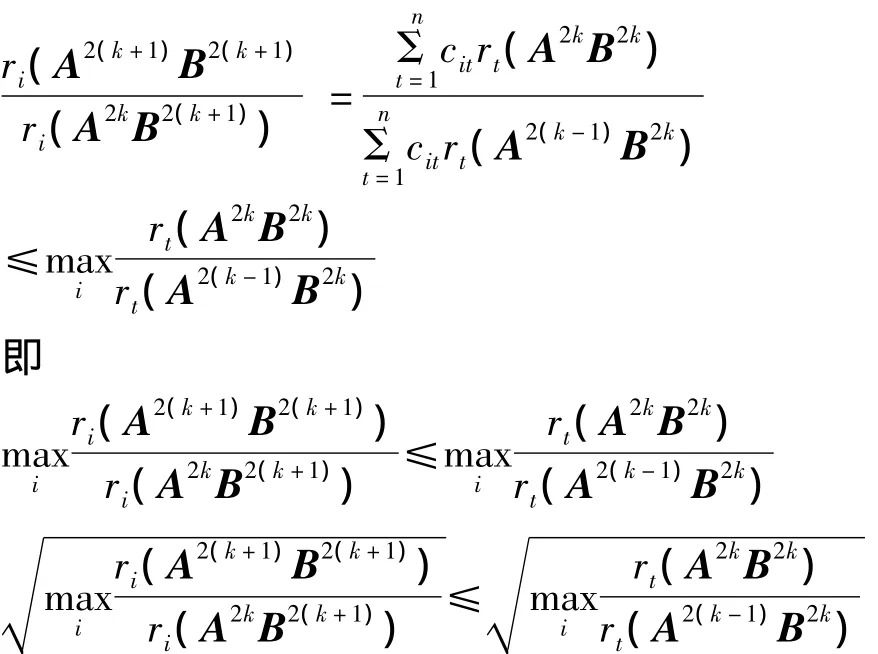

把定理2中的行和改成相应的列和,结论依然成立.
若A是n(n≥2)阶非负可约矩阵,则由文献[2]中的§3知存在n阶置换矩阵P,使得

其中块对角线上每块Aii(1≤i≤m)或为不可约矩阵,或为一阶零矩阵.
2 数值算例

Frobenius 4≤r≤8 5≤r≤7行列Hinc 5≤r≤6.25 5.6≤r≤5.8572行列Ledermann 4.1547≤r≤7.8661 5.0800≤r≤6.9259行列Ostrowski 4.5275≤r≤7.6547 5.2247≤r≤6.8165行列Brauer 4.8284≤r≤7.4642 5.3722≤r≤6.7016行列引理1(k=2)5.7335≤r≤5.7564 5.7349≤r≤5.7484行列定理1(k=2)5.7411≤r≤5.7424 5.7416≤r≤5.7417行列
与引理1相比,定理1估计精确度大有提高,且逼近的速度较快.
[1]MINCH.Nonnegative Matrices[M].New York:Wiley,1988.
[2]殷剑宏.非负矩阵最大特征值的新界值[J].数值计算与计算机应用,2002,23(4):282-295.
[3]LIU SL.Bounds for the greatest characteristic rootof a nonnegative matrix[J].Lin.Alg.Appl.,1996,239:151-160.
