定积分问题的数值求解及Matlab实现

张长耀，刘秀丽

(西藏农牧学院公共教学部，西藏林芝860000)

实际问题当中常常需要计算积分.依据人们所熟知的微积分基本定理，对于积分I=，只要找到被积函数f(x)的原函数F(x)，便有下列牛顿—莱布尼茨公式:

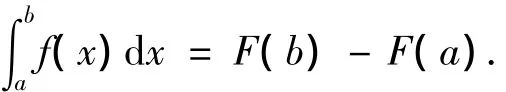
但实际使用这种求积方法往往有困难，因为大量的被积函数，诸如等，其原函数不能用初等函数表达，故不能用上述公式计算.下面我们用教学中遇到的一个定积分的题目作为例子，来说明此类定积分题目的求解.

例[1]求定积分

虽然这个题目的被积函数是形式较简单的初等函数，但它的原函数不是初等函数，无法利用牛顿——莱布尼茨公式计算.本文引入数值方法，借助Matlab编程来计算该定积分的近似值.

求解定积分的常用数值方法有矩形法、梯形法和抛物线法，下面我们借助Matlab编程分别实现.

1 中点矩形法

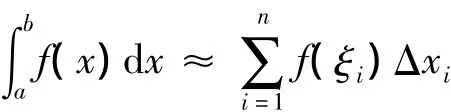
在Matlab程序中，我们将[a，b]n等分，对等分区间

在区 间[xi-1，xi]上 取 中 点， 即 取，用该积分和作为定积分的近似值.

现就上面题目给出用中点矩形法求解的Matlab程序

由程序计算得该定积分的近似值为

s=5.730 296 683 541 563.

用该方法解决此定积分题目的误差分析可以用下面定理估计.

定理1[2]设函数f(x)在闭区间[a，b]上连续，在开区间(a，b)内至多有限个点外处处有连续的导数，且存在正数M使得，用一组分点

把[a，b]n等分，则

矩形法的Matlab编程实现简单，但效果欠佳.如果在分割的每个小区间上采用一次或二次多项式来近似代替被积函数，那么可以期望得到比矩形法效果好得多的近似计算公式.下面介绍的梯形法和抛物线法就是这一指导思想的产物.

2 梯形法

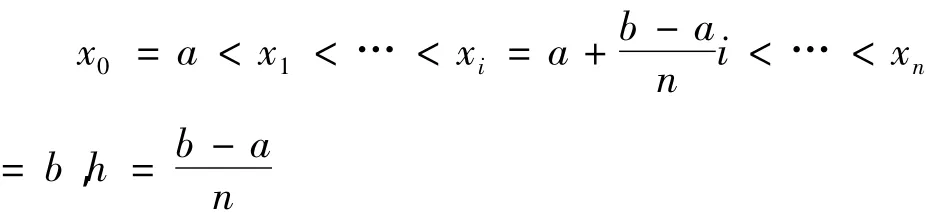
曲线y=f(x)上相应的点为

P0，P1，…，Pn(Pi(xi，f(xi))，i=0，1，…，n)

将曲线的每一段弧Pi-1Pi用过点Pi-1，Pi的弦Pi-1Pi(线性函数)来代替，这使得每个上的曲边梯形成为真正的梯形，其面积为

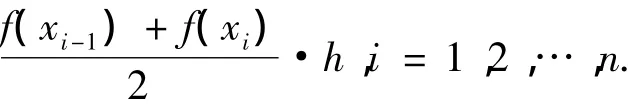
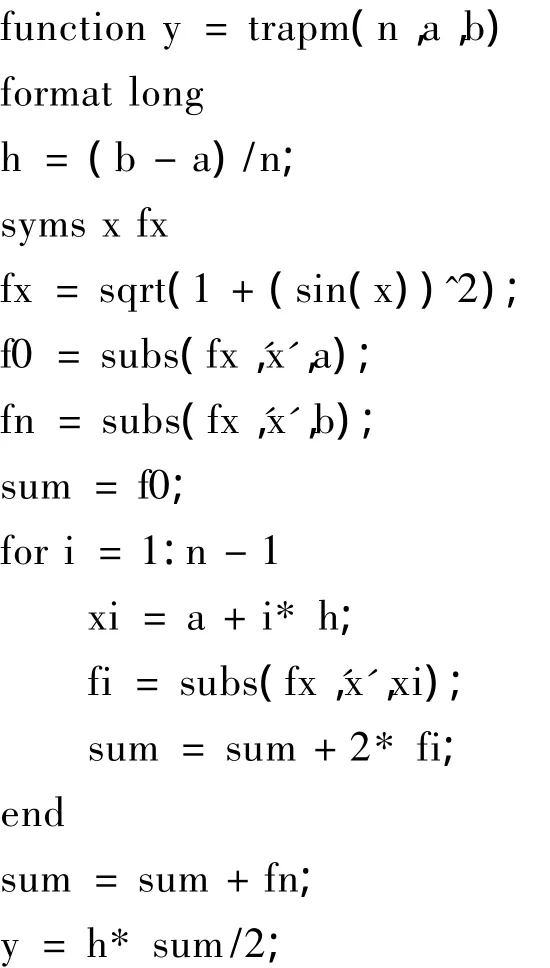
matlab命令行中输入trapm(10 000，0，3*pi/2)，即把分为10 000个子区间，由程序计算得该定积分的近似值为5.730 296 683 541 554.

用该方法解决此定积分题目的误差分析可以用下面定理估计.

定理2[3]设区间[a，b]划分为宽度为h=(b-a)/n的n个子区间，组合梯形公式

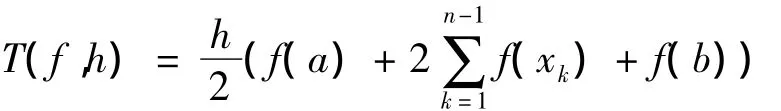
是对积分

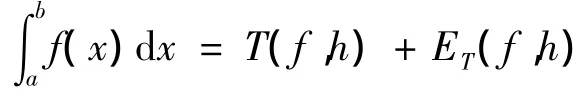
3 抛物线法(辛普森公式)

对于精度要求不是很高的定积分的计算，梯形公式的计算结果完全可以达到应用的精度要求.如果对精度要求较高，则有必要引入更有效的抛物线法，即在分割的每个小区间上采用二次多项式来近似代替被积函数.

将积分区间[a，b]作n(其中n为偶数)等分，分点依次为

曲线上相应点为P0，P1，…，Pn(Pi(xi，f(xi))，i=0，1，…，n)现把区间[x0，x2]上的曲线段y=f(x)用通过三点P0(x0，f(x0))，P1(x1，f(x1))，P2(x2，f(x2))的 抛物线

来近似代替，则有

同样也有

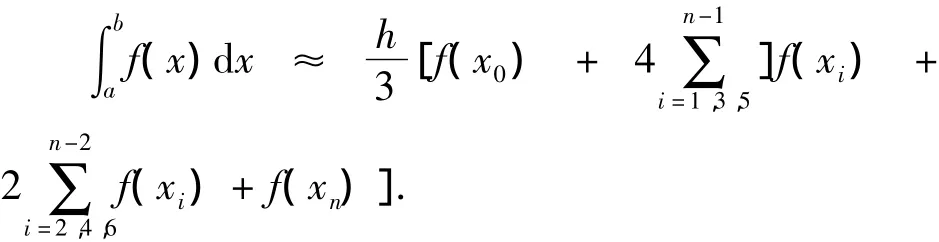
下面给出该题目用抛物线法求解的Matlab程序

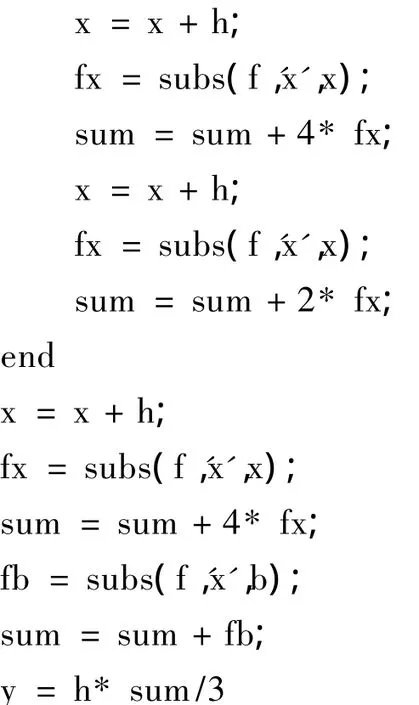
Matlab命令行中输入simeq(10 000，0，3*pi/2)，即把分为10 000个子区间，由程序计算得该定积分的近似值为5.730 296 683 541 416.

用该方法解决此定积分题目的误差分析可以用下面定理估计.

定理3[3]设[a，b]划分为宽度为h=(ba)/(2n)的2n个等宽度子区间[xk，xk+1]，组合辛普 森 公 式是积分的逼近.并且，如果f∈C4[a，b]，则存在 ξ，a＜ ξ＜b，使得误差项ES(f，h)具有的形式.

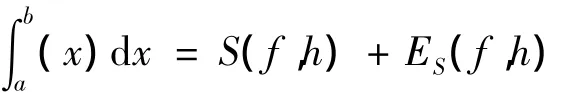
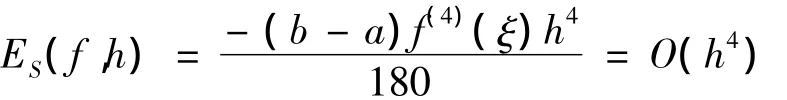
一般地，对于很难或者完全无法直接积分的复杂函数，解析方法通常是不实际的，而且有时候根本无法得到结果，这种情况，我们都可以通过本文中类似的Matlab编程的方法得到积分的近似值.

[1]张嘉林.高等数学[M].北京:中国农业出版社，2008.

[2]刘 证，丁桂艳.关于定积分几种近似计算的误差估计[J].鞍山科技大学学报，2003，26(4):313－317.

[3][美]MATHEWS JH，FINK K D.数值方法(Matlab版)[M].周 璐，陈 渝，钱 方，等，译.北京:电子工业出版社，2009.