基于初等微积分和解析几何的C方法

胡燕芳

（电子科技大学，四川 成都 610054）

基于初等微积分和解析几何的C方法

胡燕芳

（电子科技大学，四川 成都 610054）

Chandezon的基于坐标变换的微分方法（C方法）是最简单和最通用的方法之一。然而，迄今为止，只有少数的人使用它，可能是因为，它是用传统的基本张量理论进行阐述的。文章重新阐述了C方法，而没有使用任何的张量理论方面的知识，这样可以使光学工程师更容易理解。

初等微积分；解析几何；C方法

1 C方法的描述

1.1 问题描述及其符号表示

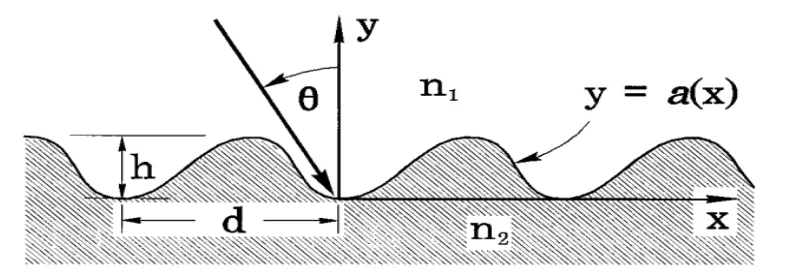
图1-1 直角坐标系下光栅结构的符号表示

我们考虑表面起伏光栅最简单的情况，如图1-1所示。周期性波纹界面在z方向保持不变，将两个各向同性的媒质分开。入射媒质的折射率n1为实数，另一个媒质的折射率n2可以为复数。我们认为两个媒质的相对磁导率 同真空中的一样，入射角为 。光栅轮廓函数y=a(x)要求连续且单值，光栅周期和深度分别用d和h表示。为方便起见，我们仅考虑TM波。如果想得到TE波的对应结果，仅需做如下变化：E↔H,ε0↔ −μ0,ε↔ −μ。这里，我们仅使用一个坐标系——笛卡尔坐标系。

图1-2 空间域D+，D−， 1D， 2D和 0D的定义

为了精确地说明光栅问题，需要做一点准备。图1-2中，两条虚线通过轮廓函数 ()a x的最大值与最小值，把空间分成三部分：1D，2D，0D。D±表示位于轮廓函数 ()ya x= 之

上与之下的半空间。根据麦克斯韦方程，我们可以很容易得到波动方程：

其中F=Hz，k0=2π/λ， 是真空中的波长。 是相对介电常数，D−：ε=ε1=n12/μ，D+:ε=ε2=n22/μ。D1，

D2中的场按瑞利展开为：

其中

是幅度常量。为了使衍射场在y=±∞有限，我们必须取= 0 ,m≠ 0 。= 0，m取任意数。为简便起见，我们规定。确定未知系数A(p)，需要m把 D1， D2区域联系起来。一般而言，在 D0区域，瑞利展开是无效的，它将 D1， D2区域分开，并且与D+，D−区域部

分重叠。光栅问题在于在D+，D−区域求解亥姆霍兹方程，使它在无穷远处和沿着 y = a ( x)服从边界条件。

1.2 算法思想

特征方程及总场表达

我们考虑D+或者D−区域中的式子(0-1)，做如下变量代换：

根据求偏导数的链式法则，有：

其中/ada dx=˙。把式子(0-6)带入(0-1)中，得到如下微分算子：

为方便起见，我们用 代替v，因为 = v 。空间变量、u具有良好的特性：当 在一个光栅周期内变化时，u保持为常量，点(x, u)所描绘的曲线平行于光栅的轮廓，因此为常量。尤其是 u = 0即为原来的光栅表面，而这一特点对坐标(x, y)并不适用。

现在，我们继续特征值问题的推导。二阶微分方程L ( ∂ v, ∂ u ; x ) F = 0 可以写成一阶方程组：

其中 F'= ( 1/i)∂ F / ∂u 。因为微分算子的系数与u无关，我们认为F、 F'依赖于指数函数exp(iρ u)。把a˙展开为傅立叶级数，进而可以将式子(0-8)转换为傅里叶空间的矩阵方程。这意味着做如下变化：

相应地式子(0-8)可以写成以下形式：

其中 β(p)是以为元素的对角阵，F和 F'是由F和 F'的傅里叶系数组成的列向量，α是以mα为元素的对角阵，a˙是由a˙的傅里叶系数组成的矩阵，即：

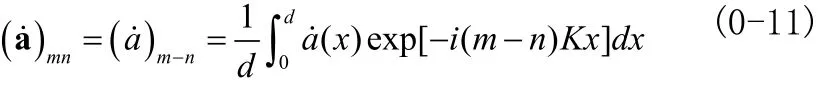
值得注意的是a˙a˙是矩阵的平方（不是矩阵(a˙)2）。当光栅具有陡峭的边缘时，式子(0-10)可以确保数值快速收敛。对左边的系数矩阵求逆，这个相对来说比较简单，因为它是对角阵，我们得到C方法的特征方程：

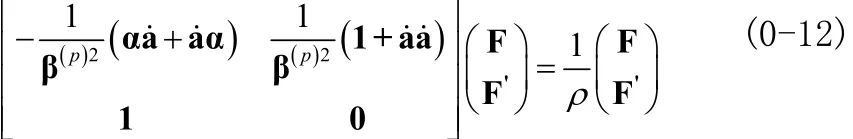
我们需要求解两个特征值问题，即当 p =1时和当 p =2时。式子(0-12)同以前的C方法中的特征方程不同。我们现在使用式子(0-12)是因为我们认为跟老的特征方程相比，它具有一定的优势。

为了求解特征值问题，需要截断这一无穷矩阵。我们假设2×2分块矩阵的每一子块被截断为N×N的矩阵。2N个特征值可以分为两组，每组中包含N个特征值。第一组，∑ +中包含正的实特征值和虚部为正数的复特征值。第二组，∑−中包含与其符号相反的特征值。每组中，把实特征值和复特征值分开。实本征解与近场和远场有关，复本征解只与近场有关。在D+区域中，应该舍弃 ∑−中除了对应入射波的特征解的其它特征解。在D−区域中，应该舍弃 ∑+中包含的解。这样做的目的是保证在无穷远处满足 OWC。严格地讲，我们应该使用符号 ∑±∑±。第一个 ± 表示与特征值相关的区域（D+或者D−），第二个±表示特征值的符号。由于舍弃了 ∑+−和 ∑−+，因此可以省略第一个上标。相应地，我们用相同的方式标记特征值和特征向量。

随着N的增加，实特征值和低阶的复特征值收敛于±β(p)（可以从表4-1和4-2中看到）。这并不奇怪，因为平

m面波是式子(0-1)的特征解，并且做变量代换并不会影响特征值。当然，可以证明满足L ( ∂ v , ∂ u ; x ) F = 0 。然而，正如以前关于C方法的文章中指出当在写边界条件时，不应该用严格的本征解，也就是瑞利平面波的解去替代式子(0-12)中的2N个解。

上面，我们假定对于任意的m， β(p)≠0。如果对于某

原则上，D+区域中的总场可以表达为入射波和 ∑+中的本征解的叠加。实际中，我们用瑞利中的相应部分来代替实本征解。这一措施与前一段落结尾描述的并不矛盾，因为只是一部分的特征解被代替。可以证明如下：数值实验说明当实本征解收敛为瑞利相应的部分时衍射效率收敛。使用瑞利解的另一原因是用空间谐波来简化特征解。因此我们可以将总磁场的z分量写为：

边界条件

式子(0-13)、(0-14)中的总场 Hz的表达式中含有变量

， ，u。因为光栅的表面可以简单地用 u = 0 来描述，为了匹配边界条件，我们仅需使用变量 和u。把式子(0-13)、(0-14)中的y用 u + a ( x)代替，并且将指数函数中的 a( x)展开为傅里叶级数。重新组合傅里叶系数，得：

对于正弦、梯形或者三角光栅mL 可以闭式表达，前者是贝塞尔函数，后者是一系列指数函数的和。对于其他的轮廓，可以通过数值积分或者快速傅里叶变换进行计算。

在 0u= 处，令F F+−= ，可得

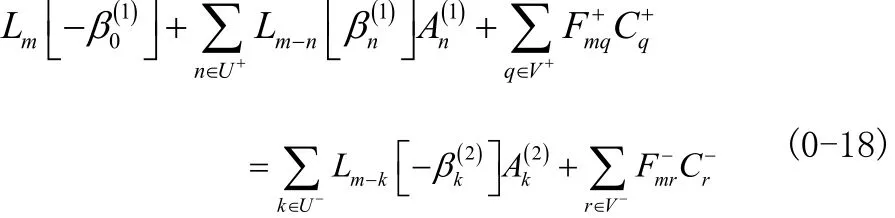
写成矩阵形式，

其中

上标R提醒我们对应的部分是瑞利解。当进行矩阵乘法时， 式子(0-18)中的n，q，k，r的总和就可得知。当截断阶数为N时，集合U+（或者U−）的传播级数和V+（或者V−）中的衰减级数的和为N。

根据初等几何学知识，我们可以得到平面曲线的切线方向，例如，光栅轮廓函数的切向分量是：

由麦克斯韦方程 ∇ ×H=−iωεε0E得

其中 Z0=(μ0/ε0)1/2，利用式子(0-6)，得到用变量 和u表示的G的表达式：

把式子(0-15)、(0-16)分别带入上式，得到G+、G−的表达式，在u= 0 处，令G+=G−，可得：

和式子(0-10)、(0-12)一样，需根据乘法规则计算a˙a˙(而不是代入傅里叶系数(a˙)2)。

合并式子(0-19)、(0-25)，得到完备线性方程组：

射级数的衍射效率ηnr和透射级数的衍射效率ηk

注意，求解TE波时，式子(0-26)、(0-29)及Z0=μ0/ε0会

有变动，具体如下

1）式子(0-26)中的ε1，ε2用− 代替

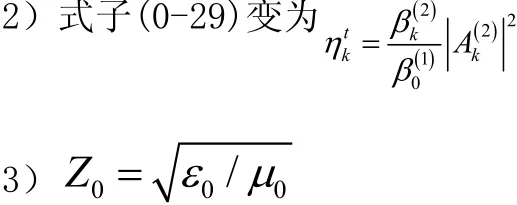
2 数值结果及其分析

这里，我们考虑等腰梯形光栅，下底角的内角60°，光栅周期 400d= nm，其他参数的设置为：入射媒质为空气，媒质2为硅（Si），入射角15θ=°，波长范围为190nm～1000nm。

图2-1、图2-2分别表示TE波和TM波的衍射效率曲线，图中的红线表示用C方法计算的结果，绿线表示用严格耦合波法（Rigorous Couple Wave Analysis, RCWA），另外一种衍射模拟算法，计算的结果。从图中可以看出：在TE波下，C方法和RCWA的衍射效率曲线是重合的，但是在TM波下，两者的衍射效率不能完全重合。

图2-1 TE波的衍射效率曲线

图2-2 TE波的衍射效率曲线

C方法和RCWA的主要区别是：

1）C方法在每种媒质中要求求解4 2N+ 阶的特征值问题，而RCWA对于每层要求解2 1N+阶的特征值问题；

2）对于TE波和TM波，C方法只需求解一个特征值问题，而RCWA对于不同的偏振态，需分别求解两种不同的特征值问题；

3）RCWA近似光栅的分界面，而C方法则不是；

4）当RCWA模拟浅斜坡的光栅或者具有很多层的多层堆叠光栅时，比如说具有大量的四分之一波层的极紫外掩模，RCWA的缺点就暴露出来了。这时分层将变得很繁琐，并且计算成本可能会大幅度增加。而C方法也具有一定的局限性，它要求光栅轮廓可以用函数来表示，并且该函数连续单值的。C方法不适用于模拟二进制模式或者轮廓陡峭的光栅。

综上所述，两种算法各有自己的优缺点。为了能有效地解决问题，我们应该采用C-RCWA相混合的方法，进而提高性能。

[1] L. Li, J. Chandezon, G. Granet, et al. Rigorous and efficient grating-analysis method made easy for optical engineers.Appl.Opt.,1999,38:304-313.

[2] J. Chandezon,D.Maystre,and G.Raoult. A new theoretical method for diffraction gratings and its numerical application.J.Opt.,1980,11:235-241.

[3] J.Chandezon,M.T.Dupuis,G.Cornet,et al. Multicoated gratings:a differential formalism applicable in the entire optical region. J. Opt. Soc.Am.,1982,72:839-846.

C method based on elementary calculus and analytic geometry

Chandezon differential methods based on coordinate transformation method ( C method) is the easiest and one of the most common method. However, to day, only a few people use it, may be it is elaborated with the traditional basic tensor theory. C method was described, without using any knowledge of theory of Tensors, it made it easier for optical engineers understand

Elementary calculus; Analytic geometry ; C method

O17

A

1008-1151(2012)06-0042-04

2012-04-20

胡燕芳，电子科技大学物理电子学院硕士研究生。