Turbo乘积码在无人机测控技术中的应用分析
2012-10-18金松坡
周 侃,金松坡
(中国电子科技集团公司第五十四研究所,河北石家庄 050081)
0 引言
乘积码是1954年由Elias提出,但当时的硬件水平限制了它的应用。1993年由C.Berrou等人提出Turbo码的概念。1994年Pyndiah等人在Chase译码算法的基础上稍加修改,提出了对乘积码的软输入/软输出次优迭代译码算法,由于这种算法类似于Turbo卷积码的译码算法,不同的是构成码由原来的系统卷积码替换为分组码。
Turbo乘积码在高码率(例如R>0.9)可以逼近仙农限,适合于高码率应用;在低码率应用时其性能已接近Turbo卷积码;在实现上较Turbo卷积码具有明显的优势。Turbo乘积码还具有延时短、译码算法能充分利用软判决、能够同时纠正随机错误和突发错误、即使在信道条件较差时仍有较好的纠错能力等优越性,都是RS码等其他编码所不拥有的。
1 Turbo乘积码的编码
乘积码按照构成子码种类的不同,可分成RS乘积码、BCH乘积码、扩展Hamming乘积码和奇偶校验乘积码。假设乘积码的子码为 C1(n1,k1,δ1)和 C2(n2,k2,δ2),其中 n、k 和 δ分别为码长、信息位长和最小汉明距离。乘积码P=C1⊗C2可以通过下面的方法得到。
①将k1*k2位信息比特按列(或者行)的方式填入k1行*k2列的数组;
②用C2码对k1行信息进行编码;
③用C1码对k2列信息进行编码。
乘积码P的参数为n=n1*n2,k=k1*k2,δ=δ1*δ2,编码效率R=k/n。乘积码的编码结构如图1所示。
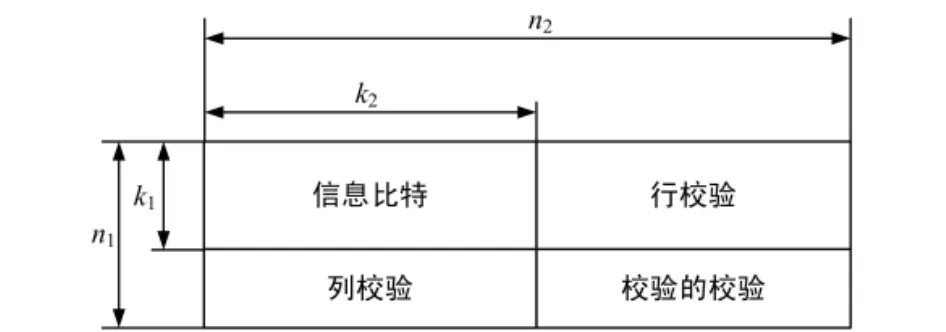
图1 乘积码的编码结构
2 Turbo乘积码的译码
2.1 Chase译码算法
通常的查表译码法属于代数译码,代数译码也叫硬判决译码。硬判决译码器的输入只有“0”和“1”两个值,这种判决结果会损失掉接收信号中所包含的有用信息。为了充分利用接收信号波形的信息,使译码器能以更大的正确概率判决接收到的码字,应把解调器输出的抽样电压的量化值送给译码器,这种译码算法称为软判决译码。
软判决的准则就是根据接收序列R,在所有码字中寻找与R欧几里得距离最小的码字作为输出。欧氏距离的计算公式为:

式中,R为具有模拟值的接收序列;C为码字(ci∈{-1,+1})。
但是随着信息位的增加,码字的数量成指数增加,译码的过程中要想搜索所有的码字将很不容易实现。Chase在1972年提出了一种简化码字搜索范围的译码算法。
Chase译码算法基于这样的思想:假设二元加性高斯白噪声(AWGN)信道中传输(n,k,δ)线性分组码字 C= (c1,…cj…cn),经调制后的发送信号为X= (x1,…xj,…xn),xj∈ {+1,-1},接收信号为R= {r1,…rj,…rn},信道噪声为均值为0、方差为 σ2的加性高斯白噪声,N=(n1,…nj,…nn),三者满足:R=X+N。对接收信号R进行最大似然译码,产生的码字以极大的概率落于以Y={y1,…yj,…yn}为中心、(d-1)为半径的球域中,d为该编码的最小汉明距离,Y为接收信号的硬判决值。
Chase译码算法的步骤如下:
①根据接收序列R,计算硬判决序列Y,其中yj=(1+sign(rj))/2,yj∈{0,1}。
②确定序列Y中的p个最不可靠位。其中p一般取2,3,4(增加p,可以提升Chase译码的效果,但是计算量会急剧增加)。序列Y中每一位的可靠度根据接收序列R计算。

式中,∧(yj)表示序列Y中第j位的可靠度。
③ 产生2p个测试图样Tq。Tq定义为一组n维向量,包括“0”和“1”在p个位置上的所有组合。
④ 构造测试序列Zq,Zq=Y⊕Tq,⊕表示按位异或。
⑤用代数译码器对Zq进行译码,也就是上述提到的查表译码法,得到输出码字Ci,并将其做如下映射:0→-1,1→+1,然后归入集合Ω。
⑥根据式(1)分别求集合Ω中的码字Di与接收信号R之间的欧几里得距离,距离最小的码字D作为判决序列输出。
2.2 硬输出到软输出
为了实现对TPC的高性能译码,必须采用迭代方式,这就要求译码器的输出为软数据,即带有可靠度度量值的数据。而Chase算法是一种针对线性分组码的软输入硬输出(Soft-Input Hard-Output,SIHO)译码算法,译出的码字为硬输出(dj∈{-1,+1})。1994年R.Pyndiah对 Chase算法做了修改,提出了Turbo乘积码的“软输入软输出”的迭代译码算法,这是一种近似的最大似然译码,能大大降低译码的复杂度。
对于软输入信号R,可以通过上述的Chase译码算法得到硬判决码字D,然后可以根据式(3)计算码字D中第j位dj的可靠度,也就是软输出。

从式(3)可以看出,计算rj'时需要2个码字C_C和D。硬判决值D是其中一个,因此需要找到另外一个码字C_C,称为D的竞争码字。C_C为码字集合Ω中与接收信号R具有最小欧氏距离并且c_cj≠dj的码字。
如果找不到竞争码字,也就是说集合Ω中所有的码字在第j位都相同,那么必须采用其他方法计算软输出信息。式(4)是一种有效的计算方法:

式中,m为迭代的次数;β为一个大于0的常数,随着迭代次数的增加而增大。β的经验取值为:
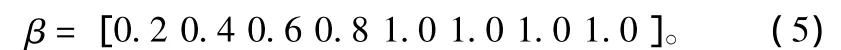
2.3 Turbo乘积码译码器
Turbo乘积码的一次完整的串行迭代译码的结构如图2所示,图中“SISO译码”表示软输入软输出译码。

图2 Turbo乘积码迭代译码器结构
图2中,[R]表示具有模拟值的接收矩阵;R[m]为外部信息矩阵,m为迭代次数。迭代译码算法的步骤如下:
①计算“行SISO译码器”的软输入值。
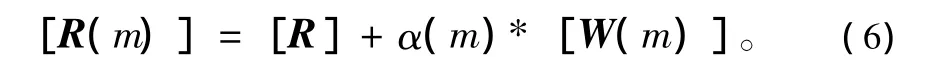
式中,α(m)为第m次迭代时的反馈系数,可以根据子码的码型和迭代次数进行调整,一般取经验值。W[m]为“列SISO译码”器经虚线反馈回来的外部信息,初始值[W(0)]=0。
②译码器对软输入矩阵[R(m)]按Chase算法逐行进行译码,计算软输出矩阵[R'(m)],并计算下一次迭代的外部信息:
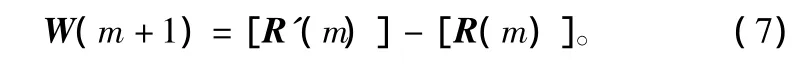
③利用外部信息矩阵[W(m+1)],按式(6)计算[R(m+1)]的值,并输入“列SISO译码”器。列译码器同样按Chase算法对[R(m+1)]逐列进行译码,并计算软输出矩阵[R'(m+1)]和外部信息矩阵[W(m+2)],然后将外部信息矩阵[W(m+2)]通过虚线反馈给“行 SISO译码”器。这样就完成了二维乘积码的一次完整的迭代译码。
迭代次数达到设定值时,将列译码器的软输出值[R'(m)]做硬判决(符号判决)后输出即可完成译码。
3 性能仿真分析
针对无人机信号参数,对信号调制方式和信道模型做如下假设:信号调制方式为BPSK;信道模型为衰落信道。在仿真中,采取C1=C2的编码方法,也就是n1=n2,k1=k2,δ1=δ2。调节参数的经验取值:α(m)=[0.0 ,0.2 ,0.3,0.5,0.7,0.9,1.0,1.0], β(m)=[0.2,0.4,0.6,0.8,1.0,1.0,1.0,1.0]。
3.1 码率对译码性能的影响
Turbo乘积码子码选取3种,分别为:
① BCH[63,51,5]*BCH[63,51,5],码率0.66;
② BCH[63,57,3]*BCH[63,57,3],码率0.82;
③ BCH[127,113,5]*BCH[127,113,5],码率0.79。
不同码率下的Turbo乘积码的译码性能如图3所示。在仿真中,采用试探序列的数目为q=24。

图3 3种码率乘积码的信噪比—误码率曲线
可以看出,码率越低TPC译码的性能越好。这是因为BCH码的码率越低,则监督位相对越多,从而可以实现更好的译码性能。译码性能对比如表1所示。

表1 误码率在10-5量级时的译码性能对比
3.2 测试序列对译码性能的影响
Chase译码选用的试探序列数目q=2p选择了3种情况进行仿真,p分别为4、3和2。图4、图5和图6分别为不同码率情况下试探序列数目对误码性能的影响仿真曲线。

图4 BCH[63,51,5]乘积码的信噪比—误码率曲线

图5 BCH[63,57,3]乘积码的信噪比—误码率曲线
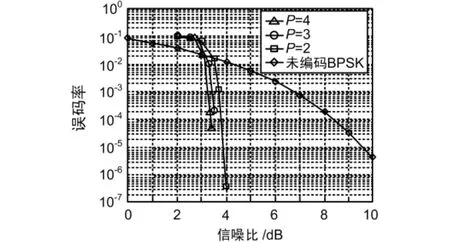
图6 BCH[127,113,5]乘积码的信噪比—误码率曲线
可以得出,测试序列越多Turbo乘积码的译码性能越好。但是,如果p取值过大,计算量就会很大,不易于硬件实现;p取值太小,译码器的译码性能变差。一般情况下p的取值为3或4即可。
4 结束语
上述对Chase算法、基于Chase算法的软输入软输出的算法进行了介绍,分析了基于Chase算法的Turbo乘积码迭代译码算法的基本结构,最后通过仿真分析了码率、测试序列个数对Turbo乘积码译码性能的影响。
Turbo乘积码在衰落信道可以获得6.0 dB左右的编码增益,测试序列选用16较合适,可以兼顾增益损失小和硬件实现简单双重要求。由于其简单的硬件实现以及较高的编码增益,如果可以应用在无人机测控领域,可以缓解机载设备资源紧张的情况。■
[1]PYNDIAH R,GLAVIEUX P A.Near Potimum Decoding of Product Codes.IEEE GLOBECOM,1994(1):339 -343.
[2]PYNDIAH R.Near Potimum Decoding of Foduct Codes:Block Turbo Codes[J].IEEE Transaction on Communications,1998,46(8):1003 -1010
[3]KIM S,OH D.Reduced-search SOVA for Block Turbo Codes[C].IEEEICC’03,2003:3076-3079.
[4]朱光喜,何业军,王 峰,等.Turbo乘积码的两种迭代译码器的比较[J].电讯技术,2004,44(6):30-34.
[5]徐友云,郭阅乐,宋文涛.次最佳软输入软输出译码算法[J].上海交通大学学报,2000(2):169-172.
[6]任卫红,叶宇煌.Turbo乘积码的软译码研究[J].通信技术,2003,36(5):44-45.
