一种基于矩阵分析的Turbo码长识别算法
2012-10-18李啸天李艳斌昝俊军杜宇峰
李啸天,李艳斌,昝俊军,杜宇峰
(中国电子科技集团公司第五十四研究所,河北石家庄 050081)
0 引言
Turbo码以其在低信噪比应用环境中所展现的优异纠错性能,在3G移动通信和卫星通信等领域得到了广泛应用。因此,在通信侦察中如何从通信信号解调之后得到的数据码流中准确快速地分析出Turbo码的编码结构及编码参数,是不可避免且亟待解决的技术问题。目前国内外有关信道编码识别技术的研究主要针对于线性分组码及卷积码,有关Turbo码的研究主要集中于其编译码性能的优化,对于其识别技术的研究还处于探索阶段。深入研究了Turbo码的归零方式和生成矩阵,提出了一种基于矩阵秩特征的Turbo码长识别算法,并通过仿真验证了算法的容错性能及识别效率。
1 Turbo码基本原理
1.1 Turbo码编码结构
Turbo码的典型编码结构为WCDMA协议中所采用的编码结构,如图1所示。

图1 WCDMA协议中Turbo码编码结构
1.2 Turbo码归零方式
归零码元为所有的信息比特经过分量编码器以后继续输入的归零比特,目的是迫使编码器回到全零状态。当k位信息码元完成编码之后首先断开第3路,输入3个码元xk+1xk+2xk+3并从第1路输出,编码器RSC1输出为zk+1zk+2zk+3;之后断开第2路,连接第3路,在编码器RSC2前输入xk+1'xk+2'xk+3'并从第1路输出,编码器输出为zk+1'zk+2'zk+3'。
下面说明Turbo码归零序列的确定。鉴于第1个编码器RSC1和第2个编码器RSC2结构完全相同,归零模式也相同,仅以RSC1的归零为例。
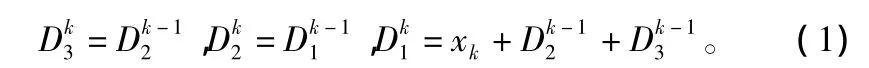
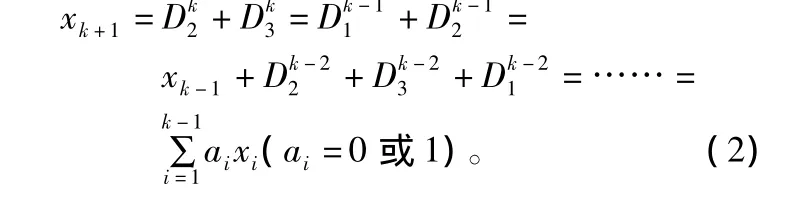
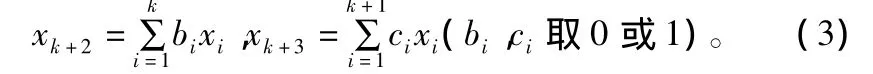
xk+3输入完成后=0,==0===0,寄存器回到全零状态。以上算法均在模2下进行。
式(2)和式(3)给出归零码元与信息码元之间的关系。其中,ai,bi,ci取值与 k有关,k确定时其取值便确定。可定义归零生成矩阵Rk为k×3矩阵,且满足=·[IkRk],Ik为k阶单位阵。假设 k=7,则
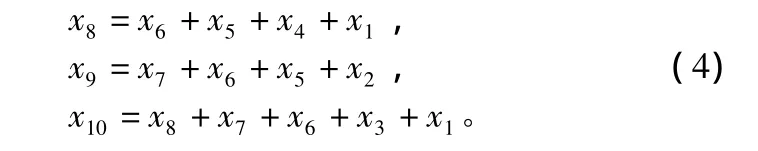
由式(4)可得:

2 生成矩阵分析
2.1 第2路生成矩阵G2
考虑图1所示分量编码器结构,设最左边加法器后的数据为uk,则有如下关系:
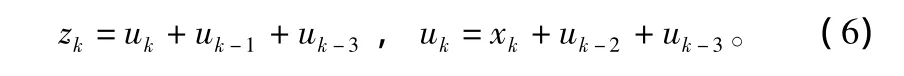
将式(6)合并:
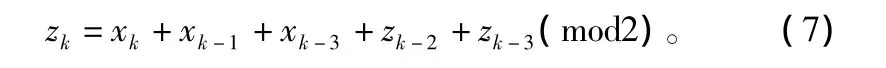
由式(7)可得:

根据上面所得输入与输出关系,可定义分量编码器RSC1的生成矩阵Tk+3为(k+3)×(k+3)矩阵(考虑归零码元),可得:


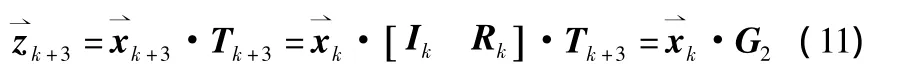
综上可得:可得G2= [IkRk]·Tk+3,为 k×(k+3)矩阵。
2.2 第3路生成矩阵G3
由于交织本身是一种数据置换,即可以用信息序列乘以初等变换矩阵来实现。如同余方程为:
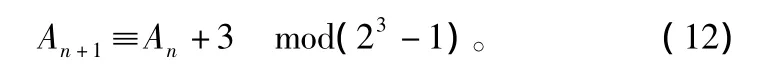
如果取A0=1,同余序列为:

利用此序列产生交织长度k=7的伪随机交织方式,交织前序列为 x1x2x3x4x5x6x7,则交织后序列为x5x1x4x7x3x6x2。此交织方式可初等矩阵表示:

定义交织矩阵Sk为k×k初等矩阵,则
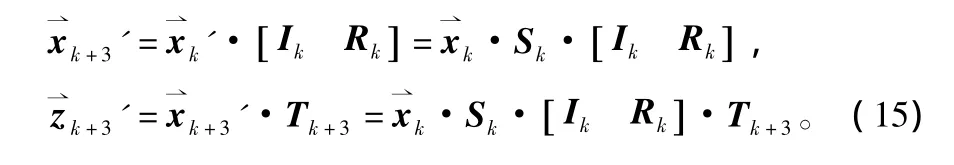
可得 G3=Sk· [IkRk]·Tk+3,为 k×(k+3)矩阵。
2.3 第1路生成矩阵G1
第1路输出为信息码元加6位归零码元。第2路归零码元的生成矩阵可直接由矩阵Rk表示。第3路归零码元在信息码元经过交织器后接入,为·Sk·Rk,可得第3路归零码元生成矩阵为Sk·Rk。综上可得第1路生成矩阵G1= [IkRkSk·Rk],为k×(k+6)矩阵。
2.4 Turbo码整体生成矩阵
G1,G2,G3中各列分别对应3路中各输出码元,将3路生成矩阵各列按照复用方式组合成为Turbo码整体生成矩阵G,可得

考虑WCDMA协议中的交叉复用模式,则由G1,G2,G3可得 Turbo码整体生成矩阵:
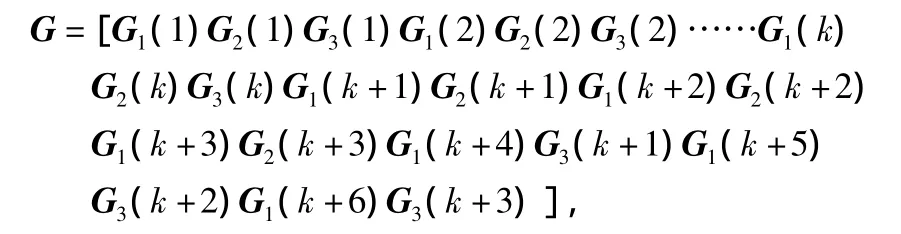
为k×(3k+12)矩阵。由此可以看出,当Turbo码的分量编码器参数、交织器参数和归零模式确定时,其生成矩阵便已确定。
由上述分析可以看出,归零Turbo码生成矩阵G不同于卷积码的半无限长生成矩阵,是有限长且固定的,因此归零Turbo码从整体的角度来看等效为一种特殊的线性分组码。考虑生成矩阵G中G1的存在,归零Turbo码还是一种系统的线性分组码。不同于一般的线性分组码,Turbo码的码长比较长。WCDMA协议中交织帧的长度k取值范围为40≤k≤5114,Turbo码长大约为k的3倍为几百至几万比特。由此可见,归零Turbo码更类似于一种特殊的LDPC码,其生成矩阵也类似于LDPC码的稀疏生成矩阵。
如卷积码定义中所述,当前码组中校验比特不仅与当前码组信息比特有关,还与之前码组的信息比特有关,而这种码组之间的影响就是由寄存器实现的,因为寄存器保留了之前码组的信息。而对于Turbo码来说,在每一帧编码完成之后对寄存器进行归零则抹去了本帧的信息,将不会对之后帧的编码产生影响,各帧按照同一生成矩阵独立编码,完全等同于线性分组码的编码特点。
对于删余Turbo码,不同的删余模式可以等效为对生成矩阵G的不同列进行删除,删除之后G仍为固定,可以认为删余Turbo码仍然等效为线性分组码,其生成矩阵为G的子矩阵。
3 码长识别
3.1 传统识别算法
将截获的码流按不同列数排列成分析矩阵,当矩阵列数正好为Turbo码长或其倍数时,由于各码组是由同一生成矩阵生成,码组之间的线性关系导致矩阵秩不等于矩阵列数,从而有如下引理[4]:
对于码长为n的线性分组码所构成的p×q矩阵(p>2n,q<p),若q为n或n的整数倍,则此时矩阵的秩不等于列数q。
3.2 改进识别算法
传统方法要求分析矩阵的行数p>2n,q<p,(q为矩阵列数,n为码长)。当n较大而q较小时,p必然较大,导致矩阵分析耗时较长。而由矩阵论的知识可知,分析矩阵的秩不可能大于q,故p对矩阵秩的影响不是很大,可适当减小以求加快识别速率,从而有如下结论:
对码长为n的归零Turbo码建立q×q分析矩阵,若q为n或n的整数倍,则此时矩阵的秩不等于列数q。
以此结论为基础改进识别算法,将识别矩阵统一为方阵,这样在q较小时将明显减小分析矩阵运算量,提高识别速率。该识别算法的具体步骤如下:
②设截获到的Turbo码流为c,从起点c1开始连续取i×i比特码元,将所取码流按行排列成i×i矩阵C,计算矩阵秩r(i)。
③ 设b(i)=i-r(i),以 i为横坐标,b(i)为纵坐标画出识别图。如识别图存在至少一根明显谱线(约为周围谱线长度5倍以上),则可认为码长已包含于内;否则i分别取+1,……,重复步骤②和步骤③继续搜索,直至满足上述条件。
④若b(i)中最大值的位置唯一,设b(i)中最大值为b1,其位置为i1,第二大值为b2,其位置为i2,若abs(i1-i2)=i1或i2,且b2也为明显谱线,则可认为码长n=abs(i1-i2)。若不满足abs(i1-i2)=i1或i2,或虽然满足但b2不为明显谱线,则可认为码长n=i1;
⑤若b(i)中最大值的位置不唯一,其位置由小到大为 i1,i2……,则可认为码长 n=i2-i1。
4 仿真实验分析
对上述识别算法进行仿真,选取交织帧长分别为40 bit、60 bit和 80 bit,得出码长识别仿真图,并采用蒙特卡洛仿真分析不同交织帧长度下识别概率与误码率之间的关系。
仿真实验1:交织帧长度k=40 bit、误码率为0.004的条件下,码长识别仿真图如图2所示。
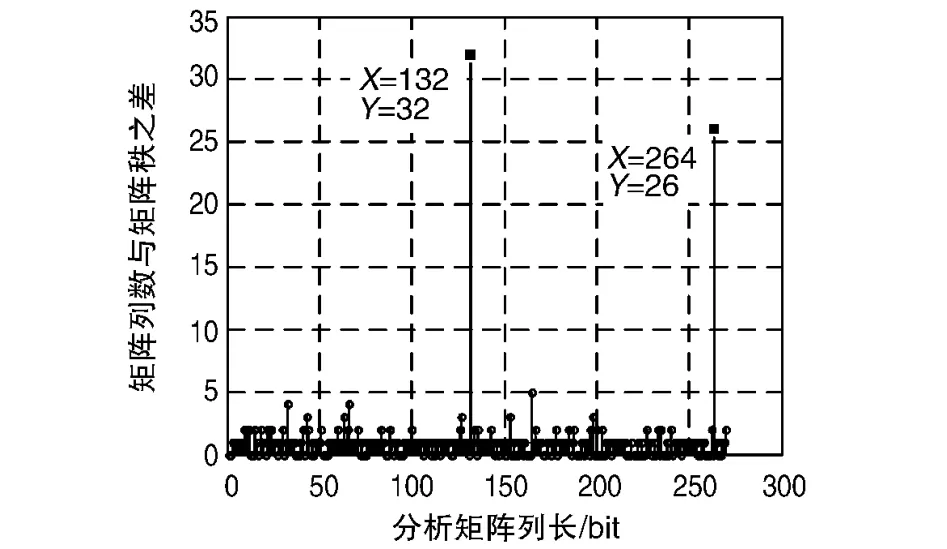
图2 k=40 bit条件下仿真
从图2中可以看出,存在2个明显谱线:i1=132 bit,i2=264 bit,abs(i1- i2)=i1=132 bit,故可认为码长n=132 bit,由前面论述可知码长n=3×k+12,可知识别结果正确。
仿真实验 2:交织帧长度 k=40 bit,60 bit,80 bit的条件下,分别对不同误码率下的识别概率进行蒙特卡洛仿真,识别概率曲线如图3所示。
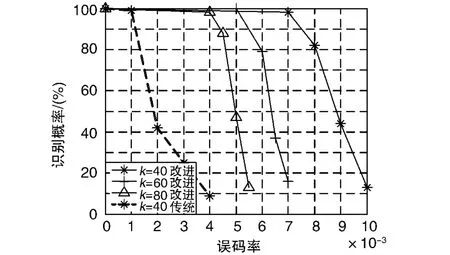
图3 各交织帧长度下识别概率曲线
由图3可以看出,识别算法在10-3误码率条件下有着良好的识别效果,交织帧长度k<80 bit、误码率小于0.004条件下识别正确率基本可达100%。随着误码率的提高,识别概率降低。同一误码率下交织长度越短(码长越短)识别概率越高,原因是在相同误码率下,码长越长,分析矩阵越大,所含误码个数越多,对分析矩阵秩的影响越大,从而导致识别概率越低;另外,由图3可以看出,改进算法在提高识别效率的同时,容错性能也明显提高,在交织帧长k=40 bit条件下,保证识别概率高于接近100%的最高误码率由0.001提升为0.007,其原因可以理解为减小了分析矩阵行数,从而降低了分析矩阵所含误码数。
由仿真可知,较之传统算法,此改进算法识别效率明显提高。在不同码长情况下,传统算法与改进算法在同一台计算机下运行耗时如表2所示。
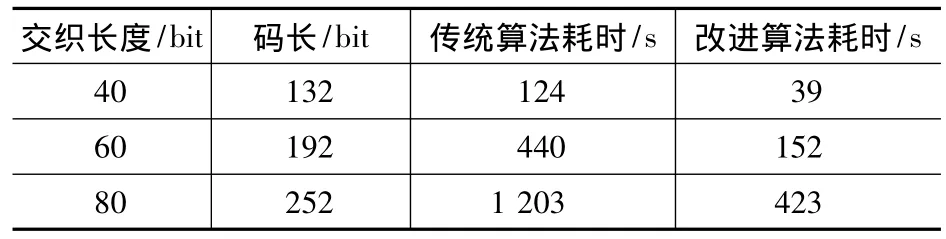
表2 传统算法与改进算法耗时比较
由表2可以看出,改进算法的运行时间仅为传统算法的1/3左右。
5 结束语
Turbo码在编码器结构上不同于一般线性分组码及卷积码,其编码结构较为复杂,故对其进行数学分析也较为困难。从数学角度推导其生成矩阵,有助于加深理解其编码特征,为其识别算法的研究提供理论基础。利用分析矩阵秩特征的方法进行Turbo码长识别,算法简单且具有一定的容错性能,但计算量偏大。通过减小分析矩阵大小,并且设置合适的判决规则可以减小计算量,提高算法运行速度,满足实际工程应用当中有效性与可靠性相统一的原则。 ■
[1]BERROU C,GLAVIEUX A,THITIMAJSHIMA P.Near Shannon Limit Error-Correcting Coding and Decoding:Turbo Codes[J].IEEE International Conference on Communication,1993(2):1064 -1070.
[2]刘玉君.信道编码[M].郑州:河南科学技术出版社,2001.
[3]王新梅,肖国镇.纠错码—原理与方法(修订版)[M].西安:西安电子科技大学出版社,2001.
[4]张永光,楼才义.信道编码及其识别分析[M].北京:电子工业出版社,2010.
[5]3GPP TS 25.212 V3.9.0.Multiplexing and Channel Coding(FDD)[S],2002.
[6]BLAHUT R.Algebraic Codes for Data Trans missiom[M].UK:Cambridge University Press,2003.
[7]昝俊军,李艳斌.低码率二进制线性分组码的盲识别[J].无线电工程,2009,39(1):19-24.
