基于粒子滤波的机载单站无源跟踪算法
2012-10-18张冠杰陈建峰李艳斌
张冠杰,陈建峰,李艳斌
(中国电子科技集团公司第五十四研究所,河北石家庄 050081)
0 引言
单站无源定位跟踪本质上是一个非线性估计问题,由于单站无源定位跟踪系统状态空间模型的非线性程度较高,以往的各种递推滤波算法,包括扩展卡尔曼滤波(EKF)和修正增益的扩展卡尔曼滤波(MGEKF)等算法,虽然可以对运动目标进行定位跟踪,但是因为经过了近似的数学处理,引起了收敛精度低和收敛速度慢的问题。近几年发展起来的粒子滤波算法是一种很好的解决非线性问题的算法,该算法基于蒙特卡洛方法和递推贝叶斯估计,其基本思想是用一个带权值的粒子集合来表示感兴趣的后验概率密度。可以处理非线性模型问题,相较于卡尔曼类滤波算法有较强的通用性,因而在导航、跟踪和监控方面得到了广泛的应用。
建立运动单站无源跟踪的系统模型,介绍粒子滤波算法的原理,并将其应用到单站无源定位跟踪中,利用仿真试验验证了粒子滤波在运动目标单站无源跟踪中的有效性。
1 系统模型
针对空中观测平台对远距离海面慢速目标的定位跟踪问题,利用载机平台上安装的干涉仪测向天线阵对目标进行定位跟踪。为了讨论方便,将模型简化为二维平面模型,如图1所示。载机沿x轴飞行,并假定方位角和相位差变化率对目标进行定位跟踪。目标沿不平行于x轴的直线运动。

图1 目标—观测器相对位置关系
根据运动学原理,目标在k时刻的状态可由k-1时刻的状态通过式(1)递推得到。模型的离散系统方程如下:

式中,Xk=[xkyk;xk和yk为k时刻目标的位置分量;和为k时刻目标在x和y方向上相互独立的速度分量;

v=[aXaY]T为协方差矩阵为Q的状态噪声。该无源定位跟踪系统的观测量包括目标的方位角和相位差变化率,其中相位差变化率可以通过测量目标的相位差而后差分滤波得到,此处认为相位差变化率信息为可直接观测量。式 (2)为系统的观测模型,其中nk=[ σφ˙σβ]T为量测噪声,表示方位角和相位差变化率的测量误差,其协方差矩阵为R。假设状态噪声与量测噪声均为零均值高斯白噪声序列且相互独立,由于目前相位差变化率估计精度有限,根据某一时刻的观测值直接对目标进行定位跟踪的精度很低,尚不能满足瞬时定位的要求,因此需要粒子滤波算法对观测量进行数据融合滤波处理,获得运动目标的轨迹信息。
2 SIR滤波算法
2.1 贝叶斯估计理论
假设动态系统描述如下:
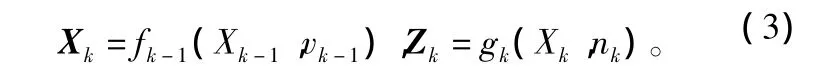
式中,Xk∈Rnx为系统状态向量;fk-1和 gk分别为系统的状态更新函数和量测函数;Zk为系统的观测量。递推贝叶斯最优估计就是要求出状态变量Xk的最小均方误差估计,即Xk后验分布的期望值。

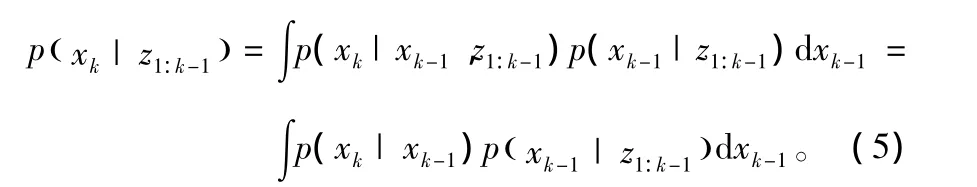
在获得测量值zk后,状态更新:
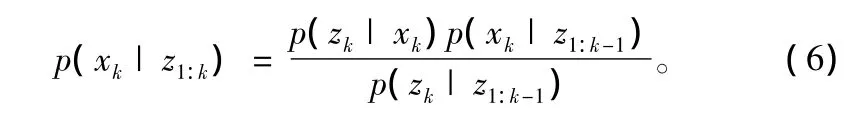
其中归一化常数为:

式(5)和式(6)构成了贝叶斯估计的基础,但是通常情况下它们没有解析解。对于非线性模型必须采用近似的数值方法来求解公式中的积分式。粒子滤波算法是一种基于贝叶斯原理的利用序贯蒙特卡洛方法生成加权粒子来描述后验概率密度的方法。
2.2 序贯蒙特卡洛方法(SIS)
序贯蒙特卡洛算法(SIS)是基本蒙特卡洛方法之一,是粒子滤波算法的基础。假设是一组取样于后验概率密度p(x0:k|z1:k)的样本点及其对应的权值,其中=1,则根据蒙特卡罗方法,k时刻的后验密度p(x0:k|z1:k)可近似为:
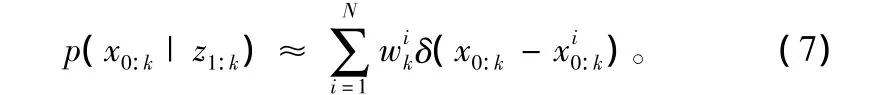
式中,δ(·)为狄拉克函数。由于无法直接从真实后验密度p(x0:k|z1:k)中抽取样本点集。因此,经常从重要密度函数q(x0:k|z1:k)中利用重要性采样的方法生成一组样本集合来描述后验概率密度p(x0:k|z1:k),则其对应的粒子权值为:

然后权值归一化为:
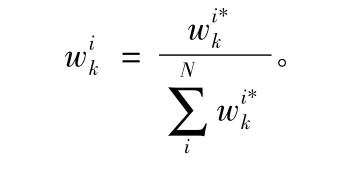
粒子滤波算法中选取重要性密度函数q(x0:k|z1:k)应该接近于后验概率分布。
2.3 SIR粒子滤波算法
在实现SIR粒子滤波算法时,主要由以下3个步骤:产生粒子、计算粒子权重并归一化和重采样。
在产生k时刻的粒子后,相应的粒子权重则由每个粒子的似然概率决定,即
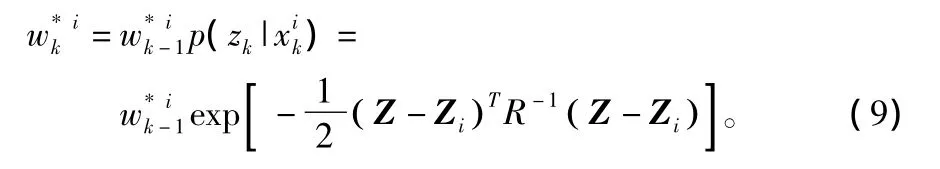
然后进行权值归一化计算。
粒子滤波随着一步一步的迭代计算,产生了粒子退化问题,因此引入重采样算法。重采样算法的基本思想是通过对后验概率密度p(x0:k|z1:k)≈(x0:k-)重采样N次,产生新的粒子集,使得p(=)=。由于重采样是独立同分布的,权值被重新设置为=1/N。重采样的步骤为:
SIR粒子滤波算法的的伪代码归纳如下:

3 仿真试验
为了验证SIR粒子滤波算法的跟踪效果,首先建立目标与观测载机的运动模型。假设运动目标的初始状态为:(100 km,20 m/s,100 km,-25 km/s),观测载机的初始状态为(0 km,200 m/s,0 km,0 m/s),为了保证载机的可观测性,观测载机与运动目标不做平行运动。滤波器的初始估计状态设定为:(100 km,0 m/s,100 km,0 m/s),测量周期为 Ts=1 s,系统状态噪声的协方差矩阵为:Q=diag([0.250.25]),量测噪声的协方差矩阵为 R=diag([0.017 0.006]),粒子数 N=3000 。进行50 次蒙特卡洛实验。在上述条件下得到EKF滤波的跟踪轨迹、粒子滤波的跟踪轨迹与真实运动轨迹的比较如图2所示。

图2 粒子滤波估计值和真实值的比较
由图2(a)和图2(b)可知,由于EKF对非线性模型采用线性化处理方法。因此,其在上述给定条件下,x方向和y方向上的位置状态量收敛速度要比粒子滤波慢,并且定位的精度也比粒子滤波低。由图2(c)和图2(d)可知,EKF算法在x方向和y方向上的速度状态量的收敛速度也要比粒子滤波慢。
为了对PF算法和EKF算法在估计偏差方面的性能进行更加严格的比较,二者关于目标位置状态分量的均方根误差(RMSE)如图3所示。
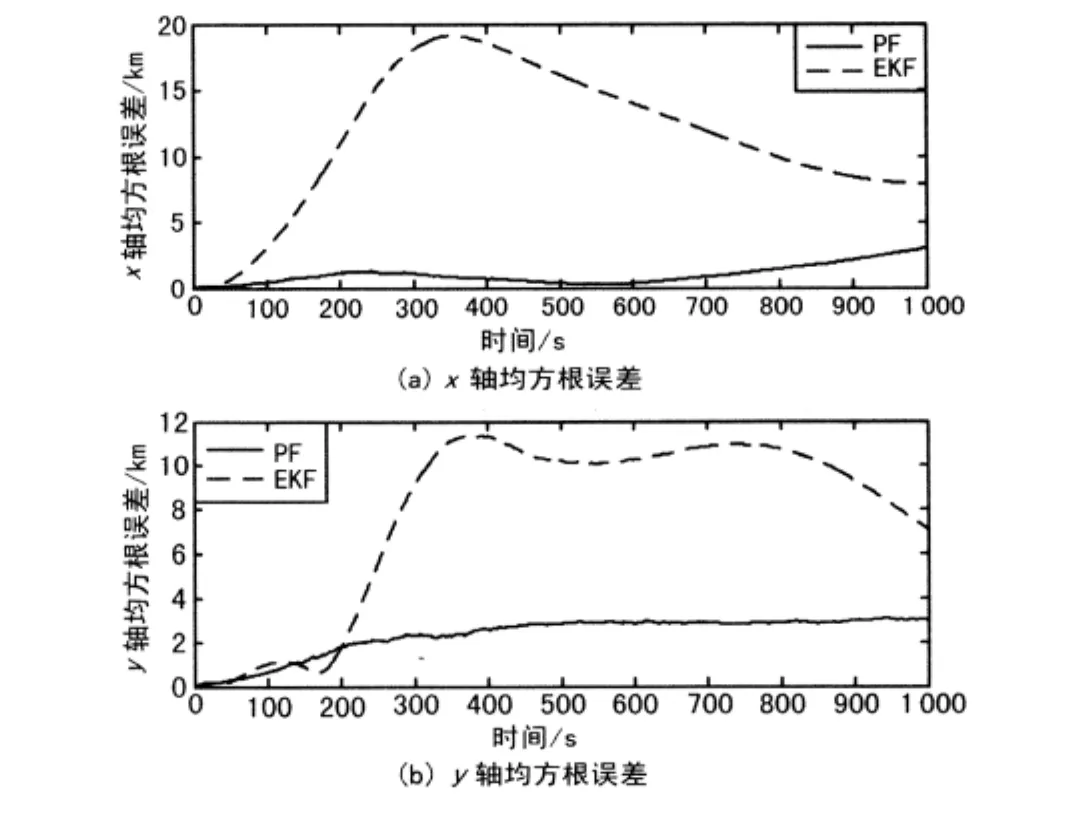
图3 PF与EKF估计的RMSE比较
RMSE的估计式定义为:

式中,Nm为Monte Carlo仿真次数。由图3可以看出,PF算法收敛快,位置状态分量可以很快地收敛到一个平稳的值。相反EKF算法的收敛偏差较大,而且收敛的速度比较慢。虽然PF与EKF均是有偏估计,但是EKF的估计偏差是远远高于PF算法的。图3更好地显示了PF算法在估计偏差方面的优越性。
4 结束语
基于蒙特卡洛思想的粒子滤波算法完全突破了卡尔曼滤波理论框架,对模型的非线性不敏感,既不用对非线性模型本身进行任何近似处理,也无需计算模型的雅克比矩阵,并且对系统的过程噪声和量测噪声没有任何限制,因此粒子滤波比EKF有更好的适应性。粒子滤波是用足够数目的加权粒子来直接近似状态量的后验概率密度,计算简单,其在高斯噪声假设下是渐进最优的,因此粒子滤波可以获得比EKF更高的定位精度和更快的收敛速度。 ■
[1]单月晖.空中观测平台对海面慢速目标单站无源定位跟踪及其关键技术研究[D].长沙:国防科学技术大学博士学位论文,2002.
[2]ARULAMPALAM M S,MASKELL S.A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking [J].IEEE Transactions of Signal Processing,2002,50(2):174 -188.
[3]GORDON N J,SALMOND D J,SMITH A F M.Novel Approach to Nonlinear/Non-Gaussian Bayesian State Estimation[J].IEE Proc.Inst.Elect.Eng.,F,1993,140(2):107-113.
[4]GUSTAFSSON F,GUNNARSSON F.Particle Filters for Positioning,Navigation, and Tracking [J]. IEEE Transactions on Signal Processing,2002,50(2):425-436.
[5]程水英,张剑云.基于无味高斯粒子滤波的空-海BOTMA 的研究[J].现代雷达,2007,29(8):68 -71.
[6]ARULAMPALAM S,RISTIC B.Comparison of the Particle Filter with Range Parameterized and Modified polar EKF’s for Angle – only Tracking[J].IEE Proc.SPIE,2000(40):288-299.
猜你喜欢
——2022 F1意大利大奖赛
