概率统计教学研究
2012-10-17韩伟
韩 伟
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
概率统计教学研究
韩 伟
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
本人通过教学实践,深感概率统计教与学之难,通过随机变量函数的分布这一具体内容,分析了学生普遍认为概率统计比较难学的原因,探讨了概率统计课程教学内容、方法等方面的教学改革思路,以期为数学课程教学方法改革实践提供一些参考.
概率统计;随机变量;函数;教学改革
概率论与数理统计是一门十分活跃的理论性和实践性都很强的学科,其知识和方法在各个领域都有着十分广泛的应用,已经渗透到自然科学和社会科学的很多领域.在高等学校,它是理、工、农、医、经管等许多专业的一门必修基础课,正在逐渐成为文史、军事、教育等专业的选修课.通过本课程的学习,使学生初步掌握处理随机现象的基本理论和方法,培养学生分析问题和解决实际问题的能力,这一点在注重应用型人才培养的今天,显得尤为重要.概率论与数理统计与学生前期所学的其他数学课程具有不同的特点:由于随机现象的不确定性,使人感到把握不定,主要表现在概念难以建立,方法难以掌握,思维难以展开,习题无从下手等困惑.在教学中应循序善诱,层层剖析,深入浅出,学用结合.下面就随机变量函数分布的教学谈一点粗浅的体会.
1 概念理论要清楚
对于随机变量X和连续函数Y=g(X)求随机变量Y的分布函数的一般方法是FY(y)=P{Y≤y}=P{g(X)≤y},再转化成含有X的事件,利用X的分布即可求解.而离散型随机变量的分布函数或概率一般使用求和符号表示的,连续型随机变量的分布函数或概率一般使用积分符号表示的,因此又演变出了求离散型随机变量的分布函数或概率和连续型随机变量的分布函数或概率的具体方法.
1.1 对于离散型随机变量X,P{X=xi}=pi,i=1,2,…,求Y的分布.
1.1.1 若yi=g(xi),i=1,2,…,为单射时,则有

1.1.2 若yi=g(xi),i=1,2,…,不为单射时,即若xi≠xj时,不一定有yi≠yj,则应分别把那些相等的值合并,并根据概率加法公式把相等的pi相加,就得到 的分布列.
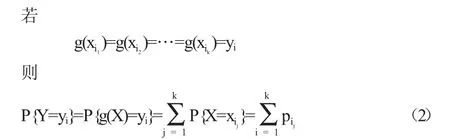
1.2 对于连续型随机变量,设p(X)为随机变量X的密度函数,Y=g(X)为连续函数,求Y的分布函数或密度函数.
1.2.1 分布函数法 也是求Y=g(X)的分布函数(或密度函数)的通用方法
a)先求Y的分布函数

b)若求Y的密度函数,需对分布函数求导

1.2.2 公式法 对于单调可微函数Y=g(X),Y的分布函数(或密度函数)可用下面公式求得

其中 x=g-1(y)是 y=g(x)的反函数,α=min{g(-∞),g(+∞)},β=max{g(-∞),g(+∞)}
在计算随机变量的函数的分布时,应注意以下几点:
1)首先要准确求出Y的取值范围.一般地,由Y=g(X)和X的取值范围即决定了Y的取值范围.但是对于离散型随机变量,要注意相同值的合并,相同值之间是“或”的关系.对于连续型随机变量,若Y=g(X)不是单调函数时,往往需要将区间化成有限个或可列个单调区间.然后在每个单调区间上应用公式;
2)应正确计算Y的分布.对于连续型随机变量X,若Y=g(X)为一般的连续函数时,要使用公式(3),先求出FY(y),再求pY(y);
3)在计算连续型随机变量X的函数Y=g(X)的分布函数(或密度函数)时,得到的往往是分段函数,一定要注意讨论.
2 例题要由浅入深,富有代表性
离散型的题目较简单,在此不述.
例1 已知随机变量X的概率密度为
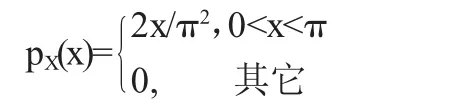
求随机变量Y=sinX的概率密度.

接下来求积分,再求导即可.
对于这样的问题,要引导学生作出图像,简单明了.
举一反三:
1)设随机变量 X在(0,π)内服从均匀分布,即 X~U(0,π),试求Y=sinX的分布函数G(y)和密度函数g(y).(课本的练习题)
2)设随机变量 X 在(-π/2,π/2)内服从均匀分布,试求Y=CosX的密度函数fY(y).

例2 对球的直径X做近似测量,设其值均匀分布于区间[a,b],试求球体积Y的密度函数.
实验仪器:H 2 S检测仪:PN-2000在线式H 2 S检测仪;反应釜:江苏海安石油科技耐高温高压抗腐蚀不锈钢反应釜;p H计:上海雷磁PHBJ-260便携式p H计。

又如:设一设备开机后无故障工作的事件X服从指数分布,平均无故障工作的时间EX为5小时,设备定时开机,出现故障时自动关机,而在无故障的情况下工作2小时便关机.试求该设备每次开机无故障工作的时间Y的分布函数FY(y).
例3 设随机变量X的分布函数FX(x)为严格单调连续函数,证明Y=FX(X)服从均匀分布.
说明:当 y<0 时,FY(y)=0,当 y≥1 时,FY(y)=1,当 0≤y<1时,

这个例子说明一维连续型随机变量不同的密度函数p(x)可以对应同一个分布函数FX(x).另一方面,这是一个十分典型的例题,可以有多种变形,如:
1)设随机变量X服从(a,b)上的均匀分布,令Y=cX+d(c≠0).证明Y服从均匀分布.
2)设随机变量X服从参数为2的指数分布,Y=1-e-2x,在区间(0,1)上服从均匀分布.
例4 设随机变量X服从 (-1,1)上的均匀分布,Y=sgnX,求Y的概率分布.
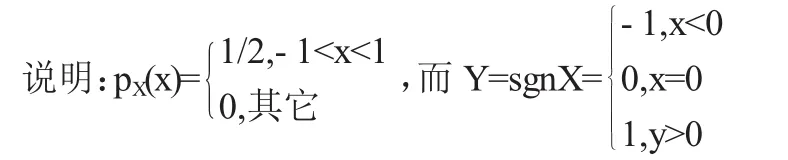
又如:设随机变量X服从(0,2)上的均匀分布
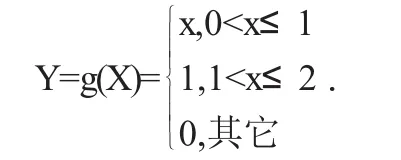
求Y的分布函数.
显然,Y不是离散型随机变量,Y也不是连续性随机变量.Y的分布函数FY(y)在Y=1处不连续.
在教材中,一般只讨论离散型随机变量和连续型随机变量,在二者之间还有一种随机变量,由于本身较复杂,应用也少,故没有讨论.对于随机变量函数,若随机变量是离散型的,其函数一定是离散型的;若随机变量是连续型的,其函数也可是离散型的,也可是连续型的,也可是非离散非连续型的.
概率统计来源于生活,具有深厚的应用基础,其有些内容使人感到是实践经验的总结,有点像文科课程,而不像数学;另外,它又具有严密的理论体系,抽象,难于理解.正是这种二重性,使概率统计成为难教难学的“边缘”学科,因此,在教学上要把握好利用好它的特点,应用性强,要结合实践来学,学以致用;理论性强,要把握住它的整体框架,在这个框架下找准用好每一个概念、定理、公式,并掌握好它们之间的区别和联系.
概率统计讨论的是不确定性问题,它的理论、方法和思维方式与以往所学的确定性理论都有很大的不同,学生感到很陌生,难以理解,无从下手,因此,教学中要注重概念的交代和比较辨析,注重理论的严密和实用,注重方法的演示和训练.循序渐进,由浅入深,层层剖析.使学生掌握好概率统计这个无处不用的“万能”工具.
〔1〕沈京一.概率论与数理统计[M].北京:高等教育出版社,2008.
〔2〕王丽霞.概率论与数理统计[M].大连:大连理工大学出版社,2010.
〔3〕茆诗松.概率论与数理统计[M].北京:高等教育出版社,2005.
O21
A
1673-260X(2012)03-0006-02
