匈牙利法中试指派的标记法

徐玲，肖双喜

匈牙利法中试指派的标记法

徐玲，肖双喜

介绍匈牙利法的数学模型及基本步骤，对匈牙利法中试指派现有的改进方法进行了探讨，提出了新的改进方法——标记法。经验证，标记法是有效而简单易用的方法。

指派问题；匈牙利法；标记法

指派问题属于0-1整数规划问题，是一种特殊的线性规划问题，可以用求解线性规划的单纯形法求解，但是因为其变量过多，用单纯形法求解就显得非常复杂。库恩（W.W.Kuhn）运用匈牙利数学家康尼格(D.Konig)的一个定理“系数矩阵中独立0元素的最多个数与覆盖所有0元素的最少直线数相等”，于1955年提出了匈牙利方法［1］。匈牙利方法是求解指派问题的经典算法，但是其也存在一些不足，如计算过程比较复杂。国内学者也运用不同的思想给出了指派问题的一些解法，如叶微（2003）［2］、高兴佑（2008）［3］、贾春玉（2004）［4］等运用伏格尔法的基本思想提出了指派问题的伏格尔算法；高俊琦（2000）［5］提出了表上作业法；李苏北（2000）［6］提出了动态规划算法；孔繁利（2001）［7］提出了网络图算法，还有很多新的方法在不断地被提出。这些算法各有不同的优点，但也有其缺点，如有的算法比匈牙利法还要繁琐，有的算法不一定能得到最终的最优解。在这些求解指派问题的解法中，匈牙利方法仍然是大家推崇的最经典的解法。本文对匈牙利法中试指派过程给出了改进方法——标记法。

一、匈牙利法的方法介绍

（一）匈牙利法数学模型

该问题的一般提法是某单位有n项工作需要完成，现恰好有n个人可以完成这n项工作，由于每个人的专业水平不同，各自完成各项工作的成本为cij，要求一人只能完成一项工作，一项工作只能安排一人完成，如何安排使总的效率最高（或者所需的总费用最省）。这类最优匹配问题被称为指派问题。

(i=1,2,…,n,j=1,2,…,n)其数学模型如下：

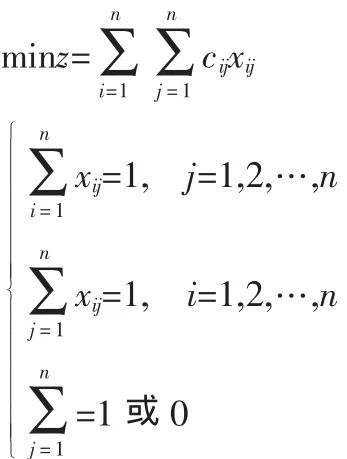
（二）匈牙利法的计算步骤

匈牙利法的基本步骤分为四步：

第一步：对系数矩阵进行行（列）变换，使各行各列中都出现0元素。

第二步：试指派。基本步骤为：在经过行、列变换后的矩阵中寻找独立0元素，若得到的独立0元素的个数等于矩阵的阶数n，则将解矩阵（xij）中独立0元素对应的元素定为1，其余元素定为0，即得到最优解。当n不大时，可以用观察、试探等简单方法准确找出独立0元素，但是当n较大时，就无法用观察、试探的方法找出独立0元素了，而按以下步骤操作：

（1）给含有唯一0元素的行(列)的0元素加圈，记为◎，该元素就是独立0元素；然后划去◎同列(行)的其余所有0元素，记为Ø。

（2）给含有唯一0元素的列(行)的0元素加圈，记为◎；将◎所在行（列）的其余所有0元素划去，记为Ø。

（3）重复进行(1)、(2)步，直至无法进行。

（4）若仍有0元素未被划圈（或划去），且与该0元素同行(列)的未被划圈（或划去）的0元素至少有两个，则从含未被划圈（划去）的0元素最少的行(列)开始，比较其所在列（行）中未被划圈（或划去）的0元素的数目，选择最少的加圈(表示选择性多的各方要“礼让”选择性少的一方)，然后划去与其同行同列的其他所有0元素。重复进行操作，直至矩阵中所有的0元素都已划圈（或划去）。

（5）若划圈的独立0元素（记为◎）的数目m与矩阵的阶数n相等，则已得最优解。若m小于n，则要转入下一步［1］。

第三步：划覆盖线，以最少的直线覆盖所有的0元素来确定该矩阵中最多能找到多少个独立的0元素。若此时覆盖线的条数小于矩阵的阶数，则要进入第四步继续进行系数矩阵的变换；若此时覆盖线的条数等于矩阵的阶数，而第二步得出的独立0元素的个数小于矩阵的阶数，则说明第二步的试指派寻找独立0元素有误，要重新回到第二步进行试指派。

第四步：继续进行系数矩阵的变换，得到新的系数矩阵，重新回第二步进行试指派。

匈牙利法的最大不足就是计算过程比较繁琐，特别是第二步进行试指派的过程非常繁琐，也容易出错误。部分学者对此进行了一些改进，但是很多改进并不成功，如学者张联朋提出了利用对角线法来快速寻找独立0元素［8］。这种方法表面看非常合理，但是在寻找独立0元素的时候，要将系数矩阵按照列向量进行重新排列，如果第一次无法得到n个独立0元素，则经历一轮调整后重新进行试指派，又要对系数矩阵按列向量进行重新排列，几个回合下来，运算者都不清楚哪一列对应哪项工作，会变得更加繁琐。学者袁迁（2007）［9］将最小元素法引入了试指派问题的求解，但是其自己在文中也提到，经过1340次的试验分析，1267次运算有效，73次无法优化，说明此种方法也存在问题。本文继续运用匈牙利方法的原理，对试指派问题提出了简洁而准确的寻找独立0元素的方法。

二、匈牙利法中试指派的改进方法：标记法

试指派是通过寻找独立0元素来完成的。库恩（W.W.Kuhn）在基本步骤中提到：选择性多的要“礼让”选择性少的。实际的做法就是将各0元素所在行和列的0元素个数之和进行比较，个数之和较大的要“礼让”最小的，即个数之和最小的那个就做为独立0元素。本文的方法就是将每个0元素所在行和列的0元素之和求出，并将数字写在该0元素的右上角，以便于比较。这种试指派的方法命名为“标记法”。具体过程如下：

（1）将所在行和列中一眼就可以看出是独立0元素的0（如该行、该列只有一个0元素的0）找出，将其打圈，记作◎，将与其同行、同列的其余0元素划去，记作Ø。

（2）将其余0元素进行标记：将各0元素所在行和列的0元素个数相加，写在各0元素的右上角。

（3）将右上角标记数字最小的0元素找出，若同时有几个最小数，则可以选其中任意一个，将其打圈，记作◎。将该元素所在行和列的其余0元素划去，记作Ø。表示该人只完成一项工作，该工作只有一人完成。回到第（1）步，重复进行，直到所有的0元素都已圈出或者划去为止。

三、算例

例：求以下效率矩阵的最优解（极小值）［1］

第二步：进行试指派。

（1）将所在行和列中一眼就可以看出是独立0元素的0（如该行、该列只有一个0元素的0）找出，将其打圈，记作◎。上面矩阵中没有这样的0元素，所以进入第（2）步；

（2）将其余0元素进行标记：将各0元素所在行和列的0元素个数相加，写在各0元素的右上角。此问题进行标记如下：

（3）将右上角标记数字最小的0元素找出，若同时有几个最小数，则可以选其中任意一个，将其打圈，记作◎。将该元素所在行和列的其余0元素划去，记作Ø。本例中有3个0元素的标记最小，均为2，则可将这三个0元素中的任意一个打圈，记作◎，将其同行（同列）的其他0元素划去，记作Ø，结果如下：

（4）回到第（1）步，因为剩下的0中不含所在行和列只有一个0元素的0，且刚才被圈出的两个0不对其他各0的标记产生影响，所以剩下各0的标记不变，直接进入第（3）步，得：

因此步被圈出（或划去）的0元素影响了其他未被圈出（或划去）的0元素，则将他们的标记修改为：

（5）将右上角数字最小的0元素找出，将其打圈，记作◎。将该元素所在行和列的其余0元素划去，记作Ø。本例中有3个0元素的标记最小，均为3，则可将这三个0元素中的任意一个打圈，记作◎，将其同行（同列）的其他0元素划去，记作Ø，结果如下：

最后还剩下两个未被圈出（或划去）的0元素，则可以将其标号抹去，直接将这两个中的任意一个圈出，而将另一个划去，结果如下：

此时，独立0元素的个数为4个，少于矩阵的阶数，进入第三步。

第三步：划覆盖线，以最少的直线覆盖所有的0元素，结果如下：

第四步：将打√行的各元素-2，打√列的各元素+2，得新的矩阵如下：

第五步：重新进行试指派如下：

（1）将所在行和列只有一个0元素的0找出，将其打圈，记作◎。上面矩阵中没有这样的0元素，所以进入第（2）步；

（2）将其余0元素进行标记：将各0元素所在行和列的0元素个数相加，写在各0元素的右上角。此问题进行标记如下：

（3）将右上角标记数字最小的0元素找出，若同时有几个最小数，则可以选其中任意一个，将其打圈，记作◎。将该元素所在行和列的其余0元素划去，记作Ø。本例中有2个0元素的标记最小，均为2，则可将这2个0元素中的任意一个打圈，记作◎，将其同行（同列）的其他0元素划去，记作Ø，结果如下：

此时第一列的一个0元素被圈出，另一个0元素被划出，被划去的0元素影响了其同行的0元素的标记，则将此0的标记由3改为2，其余0元素的标记不受这二个0元素的影响，则继续找标记最小的0元素，仍有2个标记最小的0元素，标记为2，则将其任意一个圈出，结果如下：

此时第一行的一个0元素被圈出，另一个0元素被划去，被划去的0元素影响了其同列的0元素的标记，则将其同列的0元素标记各减1，即第四列下面两个0的标记分别由5变为4和由4变为3，继续对上面矩阵找标记最小的0元素，即有标记为2的0元素，将其圈出，结果如下：

此时第四列的一个0元素被圈出，成为独立0元素，另一个0元素被划去，被划去的0元素影响了其同行的0元素的标记，故将其同行的0元素的标记各减1，均变为3。，此时还剩4个为被圈出（或划去）的0元素，其标号相同，且四个0分别位于对角线位置，则将其中处于对角线的任意两个圈出，另外两个划去即可。结果如下：

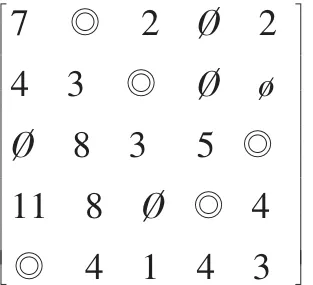
此时找出5个位于不同行不同列的独立0元素，且独立0元素的个数m等于矩阵的阶数n，则得最优解，相应的解矩阵为：

该问题的最优值为：7＋6＋9＋6＋4＝32。 结果完全正确。

四、结论

1.计算结果与库恩（W.W.Kuhn）的匈牙利法计算结果完全相同。标记法试指派的思想来源于原匈牙利算法，也表明了这种方法的正确性。

2.标记法采取将矩阵中每个0元素标记的方法来确定独立0元素，使初学者容易理解且容易操作。

3.当遇到标号最小的0元素多于一个时，可以选取其中的任意一个进行标号，此时说明该问题有多重解。

[1]运筹学教材编写组.运筹学[M].北京:清华大学出版社,2005.

[2]叶微,申卯兴,高歆,程智峰.求解指派问题的伏格尔方法[J].陕西师范大学学报：自然科学版,2003(2)．

[3]高兴佑,张向辉.一种基于伏格尔法的指派问题新算法[J].曲靖师范学院学报,2008(3)．

[4]贾春玉,温良.元素差额法在指派问题中的应用[J].长春大学学报,2004(2)．

[5]高俊琦.指派问题的表上作业法[J].运筹与管理,2000(1)．

[6]李苏北.一类最优指派问题的动态规划解法[J].运筹与管理,2000(1)．

[7]孔繁利,林闽.指派问题的一种网络解法[J].内蒙古民族大学学报,2001(2)．

[8]张联朋.对指派问题匈牙利解法的两点改进[J].西安航空技术高等专科学校学报,2007（1）.

[9]袁迁,刘舒燕.关于匈牙利法的优化[J].武汉理工大学学报,2007(3).

D221.1

A

1673-1999（2012）06-0101-03

徐玲（1975-），女，安徽潜山县人，硕士，安徽建筑工业学院(安徽合肥 230601)管理学院讲师；肖双喜（1974-），男，安徽省宣城人，博士，安徽农业大学经济管理学院副教授。

2012-01-10

国家人文社科基金青年项目“我国棉花产业面临的外部冲击及其纵向传导跟踪调查研究”（10CGL047)。