以数学建模活动为平台培养理工科学生创新实践能力

王义康，王航平

以数学建模活动为平台培养理工科学生创新实践能力

王义康，王航平

针对普通本科院校理工科专业教学实际，从解决创新实践能力培养的瓶颈问题入手，根据数学建模活动的特点，构建理工科大学生创新实践能力培养的实施方案。方案以数学建模为核心，将实际中的数学问题以案例形式融入课程教学、竞赛集训和科技创新活动，借助现代教育技术手段，运用启发式、探索式、研究式、问题驱动式等教学方法，培养学生创新实践能力。

数学建模；理工科学生；创造力

教育部全面启动“卓越工程师教育培养计划”，培养造就一大批创新能力强、适应经济社会发展需要的高质量各类型工程技术人才，为国家走新型工业化发展道路、建设创新型国家和人才强国战略服务［1］。发展创新教育、培养具有创新实践能力的人才是高等院校的重要使命，也是很长一段时期内高等教育发展的主要方向和最高目标。

目前在我国普通高等院校中，理科专业理论与实践脱节、工科专业实践实训中数学综合素质的缺失等问题日益突出［2］。因此，研究并构建一种依托基础课程，多数专业学生均可参与、受益面广、形式灵活、理论与实践并重、集约高效、并融入现代信息技术的创新实践能力培养方法，是当今普通高校理工科人才培养过程中的一个重要探索方向。近几年来，笔者所在学校以数学建模竞赛为载体、以数学建模创新实践活动为平台，对理工科学生创新实践能力的培养进行了大胆的探索和实践，逐步形成一条特色鲜明、科学务实、具有一定可移植性的理工科学生创新实践能力培养方法。

一、理工科专业教学特点及创新实践能力培养现状

理科作为自然科学的典型代表，通过概念、法则、性质、公式、定律、假设、定理、原理等自然科学知识的传授，培养学生科学的思想方法和良好的思考习惯。在传统教学过程中注重方法的严谨和程序的规范，以逻辑思维训练为主，创新实践能力的培养在一定程度上受到了抑制，理科大学生普遍表现为在创造性倾向方面较其它学科的大学生要低［3］。而其本质原因，是在理科专业培养计划中，普遍表现为理论课程与实验课程较多，内容比较抽象，教学方法也比较注重对抽象概念和原理加以解释，偏重于理论科学素养的培养，学生抽象思维和逻辑推理能力得到提升，但在纷繁复杂实际问题面前，却显得束手无策。在理科类学生中普遍存在着重理论轻实践，重口头、笔头，轻动手的倾向。随着社会对人才需求的多元化，这类学生由于创新实践能力欠缺在就业中处于一定的劣势。

工科是培养学生应用科学和技术的原理，来解决实际中的问题。工程师通过想象，判断和推理，将科学、技术、数学和实践经验应用到设计、制造、对象或程序的操作中。工科的培养目标是在相应的工程领域从事规划、勘探、设计、施工、原材料的选择研究和管理等方面工作的高级工程技术人才［4］。目前，工科培养计划中，多数普通本科院校过于强调工程技术型人才的培养，加强工程实践课程的比重，不惜通过减少学时的方法消弱数学、物理等基础学科的教学，致使不少工科学生对学习数学的重要性和必要性了解不够，对工科大学生需要具备的数学综合素质不了解，这不仅影响这些工科专业后继课程的教学效果，而且对学生将来在工程技术岗位上发挥主观能动性和创造性也存在潜在性的影响。工程技术原理的表达和推理、工程设计与产品制作、工程技术的创新与研究都离不开数学综合素质。

二、数学建模活动的特点

数学建模是一门十分注重理论联系实际的课程，有别于传统的数学课程，着重对学生进行严格的数学理论和技巧的训练，把对学生创新实践能力的培养作为主要任务，是实现与发挥数学应用功能的重要手段与途径［5］。数学建模指的是构建数学模型的全过程，一般来说，数学模型可以描述为，对于现实世界的一个特定对象，为了一个特定目的，根据特有的内在规律，做出一些必要的简化假设，运用适当的数学工具，得到的一个数学结构［6］。由此可见，数学建模活动开展过程中，让学生从现实世界中抽象数学模型，寻找事物发展的内在规律，是一种知识的探索和发现的过程。

数学建模活动主要包括数学建模课程的教学和与之有关的竞赛和科技创新实践活动，其主要特点表现为问题的多样性、解决方法的灵活性、应用技术的先进性和知识需求的广泛性。成功参与数学建模活动，一般需要学生具有较好的数学基础和计算机应用能力，同时需要学生具有灵活的思维和快速学习的能力。理工科专业教学计划中，普遍设置了一定比例的数学基础和计算机应用等方面的课程，这为数学建模活动的开展提供了有利条件。因此在理工科学生中大力推行以数学建模活动为平台的创新实践能力培养是切实可行的。

三、创新实践能力培养的实施方案

以数学建模活动为平台，着眼于学生创新实践能力的培养，构建较为完整的创新实践能力培养实施方案，方案的基本框架结构如图1所示。

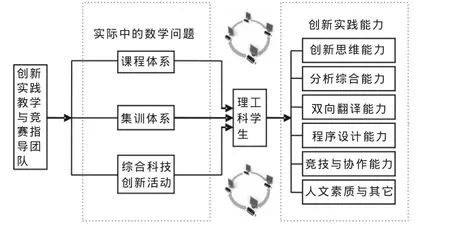
图1 以数学建模活动为平台的创新实践能力培养框架结构图

以社会对学生应用能力的需求为导向，将实际中数学问题融入到课程教学体系、竞赛集训体系和综合科技创新活动中，借助现代教育技术手段，培养学生创新实践能力，夯实数学基础，提升数学素养。具体实施方案如下：

（一）将单一的数学建模课程拓展为数学建模课程体系和竞赛集训体系

以数学建模为核心，构建以知识集群为主的课程体系，如数学建模、数学软件、数学实验、运筹学、优化理论与实践等；以知识拓展和能力提升为主的集训体系，如数学建模入门、基础知识讲座、提高专题讲座、集训综合研讨、大学生数学建模竞赛指导等。形成以数学应用、程序设计、科学研究、综合创新、系列比赛为一体的分层次、呈网络结构的综合科技创新活动体系。体系中的课程既有适合初学者的入门课，也有适合比赛需求的提高课，同时还有适合能力拓展和实践需求的专题知识讲座与软件应用课程。

（二）将实际中的数学问题融入到课程教学、集训体系和科技创新活动中

创新实践教学与竞赛指导团队结合身边实际，将身边实际中的若干数学问题，进行简化、加工、处理，凝练成为若干数学建模的教学案例，融入到课程教学、竞赛集训和科技创新活动中，吸引学生的兴趣，激发学生的创造力，提升了学生实践能力。如校车调度问题、食堂窗口优化设计问题、校内移动售货亭的设置问题、最优排课问题和奖学金名额的公平分配问题等。

（三）运用启发式、探索式、研究式、问题驱动式等多种教学方法

根据数学建模活动的特点，大力实施启发式、探索式、研究式、问题驱动式教学方法，激发学生的创造力和求知欲，将被动学习转变成为主动探究和自主学习，增强了学生的参与意识。

（四）将单一的学科竞赛拓展成综合科技创新活动

以数学建模为核心，构建综合科技创新活动体系。涵盖学生科研计划项目、新苗计划项目、程序设计大赛、开放实验项目、数学建模系列比赛等，将单一的学科竞赛拓展成为综合科技创新活动。通过学生的广泛参与，扩大了数学建模活动的受益面。

（五）利用网络平台等现代教育技术手段

理工科学生性格普遍比较内敛，很多学生不善于与他人交流和沟通。广泛利用QQ群、课程网站、协会网站等网络平台，采用网上互动答疑、设置网络讨论组等多种教学手段和方法，增强了学生参与的灵活性，激发学生学习的积极性和解决问题的创造力。

（六）建设高水平的创新实践教学与竞赛指导团队

构建一支职称比例、学历层次、知识结构合理，具有一定工程实践和指导能力、教学与科研水平高的创新实践与竞赛指导团队，发挥团队在培养学生中的主导作用。团队在教学设计、思路启迪、作品评价等方面发挥着重要的作用。

四、创新实践能力培养成效

笔者所在学校近3年参与数学建模活动的学生数显著增长，学生在全国大学生数学建模竞赛中所获得的成绩也得到大幅提升。自2009年以来，在全国、国际大学生数学建模竞赛中，取得国家级以上奖项23项，省级奖65项，总获奖率高达84%。

学校在2011年获得资助受邀参加2011年“深圳杯”全国大学生数学建模夏令营活动，获邀师生在活动中报告了论文作品，并获得了优秀论文奖，在兄弟院校中产生了强烈的反响。通过课程体系、集训体系和创新实践活动的设置与广泛开展，学生创新能力、实践能力得到大幅提升，综合数学素质显著提高。现代教育技术手段的应用，使得全校理工科专业有近33%的学生参与数学建模活动，受益学生日益增多。近3年，学校在全国大学生数学建模竞赛、国际大学生数学建模竞赛中取得的成绩，在省属高校中处于领先位置。参与过数学建模竞赛活动的学生中，有近80%的学生考入大院名校攻读研究生；参与过数学建模活动的学生，在毕业设计、就业和考研中较其他学生具有明显的优势。参与数学建模的学生中有47人次公开发表学术论文，有近1/3的学生参与各类创新科研计划项目，并有多人次获得授权实用新型专利和发明专利。与此同时，连续汇编印制学生参与数模活动心得文集《模路心语》《我的2011数模记忆》等，并拍制了多部数学建模活动记录片，丰富了校园文化，有效提升了理工科学生的人文素质。

五、结语

实践证明，以数学建模活动为平台，大力拓展和优化资源建设，充分发挥数学建模的辐射和传动作用，构建独具特色的理工科学生创新实践能力培养实施方案，开展系列科技创新实践活动，可以有效拓展学生知识面，激发学生学习的主观能动性，增强学生自主学习意识和能力，提升学生的创新实践能力。这为新时期高等教育大众化背景下如何解决理科学生理论与实践脱节、工科学生数学综合素质缺失，培养理工科学生创新实践能力，夯实工科学生数学理论基础，提升工科实践实训中的数学思维和能力，落实实践育人做出了一些行之有效的探索和实践。

[1]周英.落实卓越工程师教育培养计划大力培养科技创新人才[J].中国大学教学，2011(8).

[2]戚业国.大学创新人才培养体系改革的深层次思考[J].中国高等教育,2010(7).

[3]彭兴跃.关于理科大学生创新素质培养的思考[J].厦门大学学报，哲学社科版，2006(8).

[4]王刚.工科教育模式的改革与实践[J].高等工程教育研究，2011(1).

[5]姜启源,谢金星.一项成功的高等教育改革实践—数学建模教学与竞赛活动的探索与实践[J].中国高教研究,2011(12).

[6]姜启源,谢金星,叶俊.数学模型[M].北京,高等教育出版社,2010.

G642.0

A

1673-1999（2012）06-0176-02

王义康（1976-），男，安徽寿县人，博士，中国计量学院（浙江杭州 310018）理学院讲师；王航平（1959-），男，浙江舟山人，硕士，中国计量学院理学院副教授。

2012-01-05

浙江省教育科学规划2012研究课题（SCG35）；浙江省新世纪教学改革与研究项目（ZC2010034）。