基于复合混沌的图像空域加密新算法

崔 霄，张鹤鸣

（1.西安工业大学 计算机科学与工程学院，西安 710032；2.西安电子科技大学 宽禁带半导体材料与器件重点实验室，西安 710071）

0 引言

图像安全在设施监控和卫星通信等系统中被广泛关注。传统加密算法没考虑大数据量及高冗余度，加解密速度慢。当前数字图像加密主要采用置乱、代换和扩散三种操作。置乱打乱像素位置，代换替换像素值，扩散则是在众多像素值之间进行渗透使其相互影响。在空域使用这三种操作虽破坏了像素间相关性，但数据精度没有损失。同时算法操作较简单，计算复杂度较低。对于变换域的加密，由变换导致的数据精度损失使得它无法用于需要精确恢复明文的应用。设计加密算法时，如果没有综合使用置乱、代换和扩散操作[1～4]，或存在不动点，会使明密文对中存在不安全的线性关系。文献[1, 2]只置乱了位置，没有代换和扩散操作；文献[3]改变了像素值，但没有置乱位置；文献[4]选用N维仿射变换进行加密,没改变像素位置，求解同余方程组就能破解；文献[5]的算法只适用于长宽相等的图像。本文提出一种新的空域加密算法，更安全也更有效。

1 置乱变换

置乱变换打乱像素位置，破坏像素相关性。目前有Arnold变换及其扩展、Baker映射、幻方变换、基于随机数排序的置乱[1]等。Arnold及其扩展变换采用了矩阵变换的形式，能快速打乱像素位置。基于仿射变换的置乱使得所有像素的位置均可能发生改变，而Arnold变换不会改变(0, 0)像素的位置从而存在漏洞。基于Arnold变换、幻方变换的置乱对图像的长宽比例有限制。因此选用仿射Arnold扩展变换进行置乱能快速打乱像素，消除不动点，同时对长宽无限制。其公式如下：

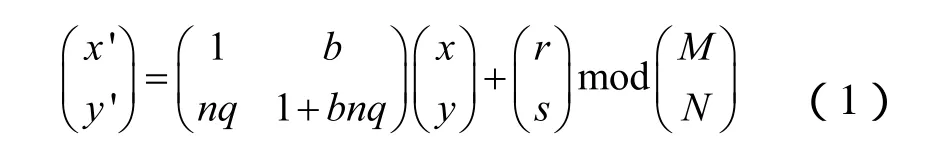
其中q＝N/gcd (M, N)；b, n, r, s均为正整数。

对 M 行 N 列图像，(x, y)和 (x’, y’)代表置乱前和后的像素坐标，该置乱变换是一一映射。

2 加密算法

将像素划分为高位平面和低位平面的两部分并连接成新图像；再通过置乱变换打乱新图像中的4比特数值并对其对其进行代换和扩散，代换和扩散过程中使用当前数据扰动复合混沌系统以引入自适应的加密，迭代2轮；将高、低平面的数据对应组合得到密文图像。具体过程如图1所示，解密为加密的逆。

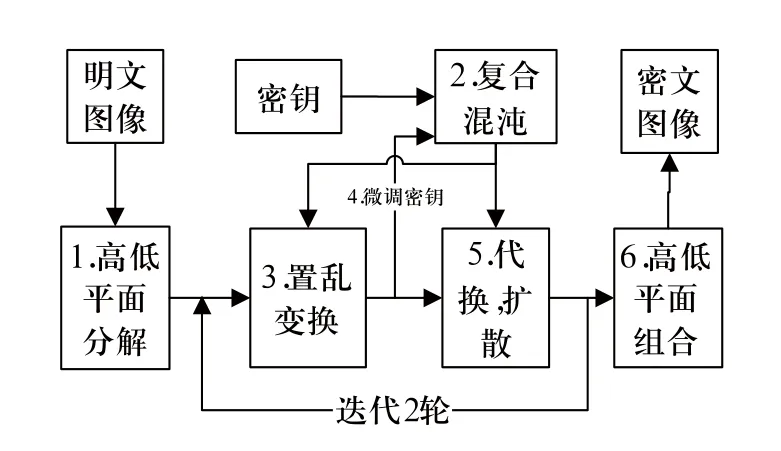
图1 加密

2.1 高低平面分解

分隔4个高位与4个低位平面，并排拼接到一起形成M行2N列的新图像，每个像素值用4比特位表示，取值[0, 15]。

2.2 复合混沌

混沌系统对初始参数极其敏感，输出伪随机噪声，适用于加密。我们采用以下3个映射构造复合混沌系统：

密钥为k1k2，k3k4。抽取对应混沌子序列小数点后1到6位形成新序列得到{xi'}、{yi'}和{zi'}；将{xi'}与{yi'}按位异或得{yi}；将{yi}作为抽样间隔对{zi'}抽样得到{zi}。

2.3 置乱变换

用 {zi}生成置乱参数，b = z5，n = z10，r = z15，s = z16，用式（1）进行置乱。

2.4 微调密钥

在保证加密可逆的前提下，用中间结果扰动混沌系统，增强安全性。在置乱变换之后，代换、扩散之前，取前一行所有像素均值IA用下式调整，形成新的混沌序列{zi}。

调整 Logistic 映射：l = [k1+(IA+ 1) / 32]/ 2，x0= [k2+ (IA+ 1) / 16]/ 2 ；

调整 Tent 映射：l = [k3+(IA+ 1) / 32]/ 2，x0= [k4+ (IA+ 1) / 16]/ 2 ；

2.5 代换、扩散

将新的4比特像素值按Ci= ((Pi+) mod 16 Å (mod 16) Å zi+) mod 16运 算，Pi为 第i个像素代换、扩散之前的值，Ci为之后的值，Å为按位异或。

2.6 高低平面组合

迭代2轮之后，分割新图像，将高低4位比特对应连接到一起形成M行N列的密文图像。

3 试验与评价

k1= 0.06，k2= 0.3，k3= 0.3，k4= 0.33， 对1024×1024大小的256色标准图man (图2)加密得图3，解密得图2。

图2 明文

图3 密文

3.1 视觉效果

3.1.1 峰值信噪比

在图像上叠加噪声，峰值信噪比为10log10/MSE)，ymax为像素的最大亮度值，峰值信噪比在20dB以下意味着完全不可辨识。微调密钥使峰值信噪比均小于8.02dB，密文图像不可辨识。

3.1.2 明密文相似度

图像相似度：1-∑∑(pij- cij)2/∑∑p2ij, 差别越大相似度越小，完全相同时相似度为1。微调密钥使相似度均小于0.09，差异显著。

3.1.3 相邻像素相关性

相关性 rxy= |Cov (x, y) | / D (x)1/2D (y)1/2，其中均值E (x)，方差D (x)，xi、yi为相邻像素值。水平相邻像素相关性为0.9932，垂直为0.9944，对角为0.9902；微调k2使三个相关性均小于0.0035。

3.1.4 信息熵

vi为L级灰度图象的第i个灰度值，P (vi)为像素所占的比例。信息熵可度量图像灰度值的分布，分布越均匀信息熵越大，最大为8。明文信息熵为7.523737，微调k1、k4、k6使加密后信息熵均大于7.999，能抵御统计攻击。

3.2 安全性分析

3.2.1 密钥敏感性

令k1= k1+ 10-15，解密图3得到图4；令k2=k2+ 10-15，解密后得到图5；密钥敏感性很强，微小改变都会导致解密失败。类似实验也可说明强密文敏感性。

3.2.2 密钥空间

密钥k1k2，k3k4为15位十进制数，密钥空间1015×6＞＞2270，大于 270 位。大大超过目前可接受的安全长度(128位)，能有效抵御穷举攻击。

4 结论

图4 微调k1

图5 微调k2

本文提出了一种空域图像加密算法，灵活使用了置乱、代换、扩散和自适应的操作。利用复合混沌系统产生置乱参数和矩阵变换的形式，快速打散像素，消除不动点。这种综合设计使得明密文间映射关系很复杂，很难进行选择明文攻击。理论分析和试验结果表明：算法密钥空间大，加密后视觉效果好，敏感性强，安全性高。进一步的工作是研究如何引入自适应更强的加密操作。

[1]MENG J L, PANG H J, GAO W Q.New color image encryption algorithm based on chaotic sequences ranking[C].Proceedings of International Conference onIntelligent Information Hiding and Multimedia Signal Processing 2008.USA.Washington D C: IEEE Press,2008:1348-1351.

[2]SHANG Z W, REN H E, ZHANG J.A Block Location Scrambling Algorithm of Digital Image Based on Arnold Transformation[C].Proceedings of The 9th International Conference for Young Computer Scientists 2008.USA.Washington D C: IEEE Press, 2008.2942-2947.

[3]BIBHUDENDRA A, SARAT K P,GANAPATI P.Image Encryption by Novel Cryptosystem Using Matrix Transformation[C].Proceedings of First International Conference on Emerging Trends in Engineering and Technology 2008.USA.Washington D C: IEEE Press,2008.77-81.

[4]WANG F C, BAI S, ZHU G B, SONG Z H.An Image Encryption Algorithm Based on N-Dimension Affine Transformation[C].Proceedings of the Eighth IEEE/ACIS International Conference on Computer and Information Science 2009.USA.Washington D C:IEEE Press, 2009.579-585.

[5]Chen D M.A Feasible Chaotic Encryption Scheme for Image[C].Proceedings of International Workshop on Chaos-Fractals Theories and Applications 2009.USA.Washington D C: IEEE Press, 2009.17.