自升式平台桩基土体变形规律与破坏机理分析＊

张其一

（1.中国海洋大学工程学院，山东 青岛266100；2.山东省海洋工程重点试验室，山东 青岛266100）

在21世纪全面开发海洋资源的时代，我国海洋工程科学应紧紧聚焦于海洋资源开发中的关键技术和科学问题，积极发现和解决开发利用中的新问题和特殊问题。自升式平台是国内外海上油气资源施工的重要设备，它具有定位能力强、作业稳定性好等优点，在中国大陆架油气资源开发中居重要地位［1］。目前，在世界范围内自升式平台作业海域涉及墨西哥湾、波斯湾、北海、远东、西非近海、以及我国渤海、东海、黄海、南海等海域。工程实践表明，海洋自升式平台工程灾难性事件，如平台倾覆、平台滑移、桩腿断裂、桩腿穿刺等，往往与海床土层的稳定性直接相关。

国外对自升式平台的研究较早，已经有60多年的发展历史，积累了较多成熟的经验，对平台桩腿与海床土的相互作用，桩周土体极限承载能力进行了较多研究（美国SNAME、英国、挪威等）［2－7］，研究方法多为实验室测试、海上现场实测和理论分析等。国内对自升式平台的研究工作还不深入、起步也较晚，尚未掌握深水桁架腿自升式平台设计的关键技术，不能满足深海采油等海洋工程日益发展的需要。事实上，自升式平台桩基的稳定性，主要取决于桩周土体的极限承载能力，因此合理而准确地对海床土层承载能力进行评估与计算，是保证平台桩基稳定性的关键。

目前，在评价研究自升式平台稳定性与桩基极限承载能力方面，国内外学者除了采用刚塑性理论推导之外，往往采用有限元方法对其进行数值研究。刚塑性理论分析法不能考虑插桩过程中土体边界的非线性变化，也不能反映土体的弹塑性应力应变关系；传统的数值计算方法一般基于物质坐标的lagrangian方法，而且土体的应力应变关系一般也是基于小变形理论进行推导，在模拟插桩过程中当桩周土体发生大变形时单元扭曲过于严重，从而导致数值计算结果失真。本文采用Hu和Randolp提出的网格重绘与插值计算RITSS方法［8］，通过对通用非线性有限元分析软件Abaqus进行二次开发，对自升式平台插桩过程中桩基土体变形规律与破坏机理进行了详细分析。

1 计算方法

1.1 大变形有限元计算方法

在利用有限元进行数值计算的过程中，一般通过荷载控制方法或位移控制方法进行加载；与荷载控制方法相比，位移控制方法能够较准确地得到基础的荷载－位移曲线。本文采用RITSS计算方法，将有限元分析过程中的大变形、大位移过程划分为一系列小变形子分析步，通过对每个小变形子分析步进行有限元网格重划和单元高斯点状态变量插值，最终实现位移加载过程的大变形分析。

计算过程中每个子分析步过程中都采用小变形的平衡方程、几何方程和土体小变形情况下的弹塑性应力应变本构方程。通过Python程序完成网格提取与重绘，并对高斯点上的应力状态进行映射与插值；利用Fortran编制计算主程序实现对Abaqus的直接调用，从而自动完成有限元计算过程的网格重绘、变量参数更新，具体计算过程见图1。

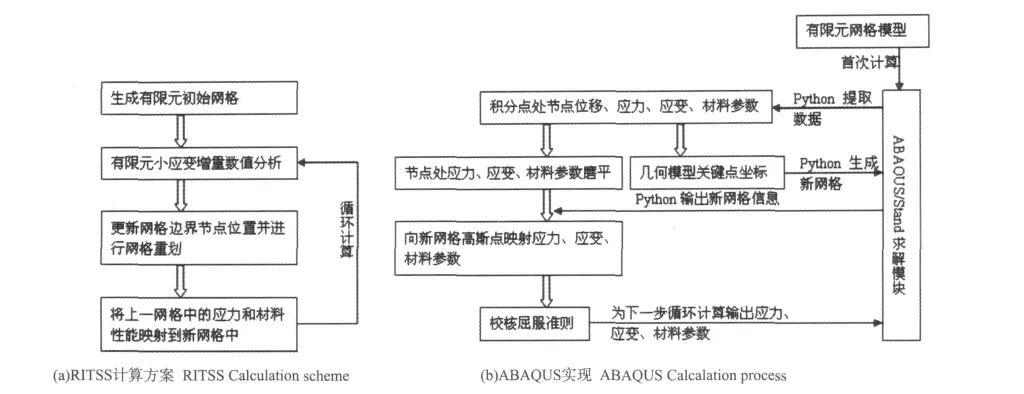
图1 RITSS计算方法Fig.1 RITSS calculation method

图2 自升式平台插桩有限元模型Fig.2 Numerical model of penetration of jack－up platform

本文基于Galerkin数值分析方法，采用图1（a）所示的网格重绘与插值技术，利用Abaqus／Stand的牛顿求解方法对平台插桩过程进行大变形分析，计算流程如图1（b）所示。有限元计算模型见图2。

有限元计算过程中，自升式平台桩腿直径取为D，利用刚性离散单元模拟；海床地基尺寸宽度取为10D，深度取为5D。不排水饱和软黏土海床黏聚力与内摩擦角分别取为Su0＝12kPa和φ＝0，弹性模量和泊松比分别取为E＝5.8×107与v＝0.49，地基中地应力系数取为1.0。针对不排水饱和土体的体积不可压缩特性，本文采用了2阶8节点杂交单元及减缩积分技术，来消除数值分析过程中完全积分单元的“剪力自锁”现象。

1.2 桩土界面摩擦特性

自升式平台预压载桩腿压入海床土体过程中，桩周土体将对桩腿表面产生摩擦阻力。该阻力沿着桩腿表面并非均匀分布，随着土体剪切应变的变化而变化（见图3）。本文采用 Wong等假定的桩土界面剪切模型见式（1）。

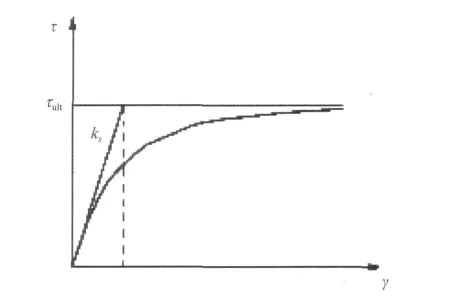
图3 桩土界面摩擦关系曲线Fig.3 Curve of friction between pile and clay

式中：γ和τ为土体剪应变与剪应力；τult为桩侧饱和不排水软粘土抗剪强度；ks为土体初始切向剪切模量。桩土界面摩擦特性通过Abaqus／Stand二次开发接口FRIC子程序来模拟。

1.3 土体抗剪强度

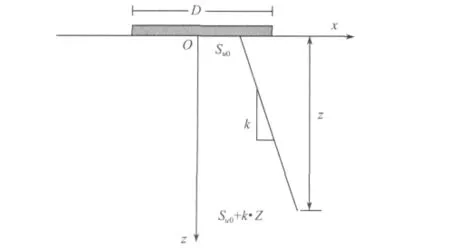
图4 非均质地基黏聚力变化关系图Fig.4 The relationship between the cohesion and the depth

本文假定海床地基土体抗剪强度随着海床深度发生线性变化，变化规律服从下式式中：Su0为海床表层土体不排水抗剪强度；k为不排水抗剪强度随海床深度变化系数；Z为海床深度，海床断面图见图4。本文利用Abaqus／Stand二次开发接口UFIELD子程序来实现。

2 数值分析

2.1 桩周土体变形规律

图5 平台桩腿插桩过程桩周土变形规律Fig.5 Clay deformation law during penetration of jack－up platform

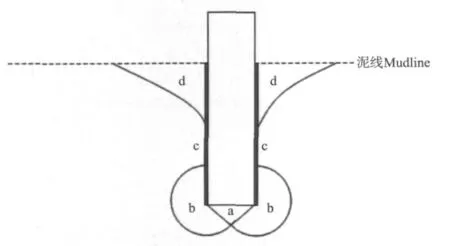
图6 桩周土体变形规律示意图Fig.6 Schematic diagram of clay deformation law

由图5所示的桩周土体位移矢量图可知，在自升式平台插桩入泥过程中可将桩周土体划分为如下4个区域：（a）桩底压密区；（b）桩端塑性流动区；（c）桩侧摩擦区；（d）桩周塑性流动区（见图6）。

随着自升式平台桩腿插入海床深度的逐渐增加，在桩底摩擦力与桩底周边土体的约束作用下，桩底压密区（a）逐渐增大，压密区土体水平向变形逐渐减弱，逐渐发展成单一的竖向变形；即该压密区土体在桩腿入泥达到一定深度后，将在基底粘聚力的作用下吸附于桩底，随着桩腿一起压入较深土层。

随着自升式平台桩腿插入海床深度的逐渐增加，桩端土体（b）在桩底与桩周土体约束下发生塑性流动；当桩腿入泥较浅时，在较小的上覆土压力作用下塑性流动区可以扩展到海床表面；随着桩腿入泥深度的逐渐增加，塑性流动区出逸点不再扩展到海床表明，而是交于塑性强度较低的桩土界面处。

随着自升式平台桩腿插入海床深度的逐渐增加，桩腿侧面与海床土体接触面积逐渐增大，出现了图6所示的桩侧摩擦区（c）。由于插桩过程中桩底以上的桩周附近土体出现严重的重塑现象，黏土结构得到破坏以及桩侧出现的超孔隙水压力不能及时消散，使得该摩擦区域抗剪强度较低。

随着自升式平台桩腿插入海床深度的增加，桩周塑性流动区（d）首先呈现被动挤压状态，在桩端塑性约束区（b）的挤压下发生被动破坏，出逸点在海床表面；随着插桩深度的进一步增大，桩端塑性约束区（b）出逸点出现在桩土界面，桩周塑性流动区（d）在自身重力与水压作用下发生回落，对桩侧产生主动土压力作用；桩周塑性流动区（d）的范围同桩侧摩擦区（c）的土体重塑抗剪强度和厚度有关。

2.2 桩周土体失稳机理

图7 平台桩腿插桩过程桩周土破坏机理Fig.7 Failure mechanism of clay seabed of jack－up platform

由图7所示的桩周土体等效塑性应变可知，饱和不排水软粘土海床在桩腿作用初期，基底土体发生整体剪切破坏，破坏模式同Prandtl破坏模式一致，包括：基础底部的主动破坏区、基础端部的扇形塑性变形区和基础外部的被动破坏区。随着桩腿贯入海床土体深度的增加，在基底上部土体的约束作用下，桩侧土体发生较为复杂的塑性破坏，被动破坏区边界已经不能在海床表面逸出，而是出现在桩土交界面上，桩周土体破坏模式不再同Prandtl模式一致。自升式平台插桩过程中桩周土体提供的极限承载能力，主要包括桩底土体的反力、桩侧土体与桩腿表面的侧向摩擦力、以及表层土体塑性回流对桩侧的挤压作用。在上述大变形有限元计算结果的基础上，可以按照图6所示的桩基土体变形规律，给出桩基土体的失稳模式，包括：桩底土体主动破坏区、桩端塑性约束区、桩侧摩擦破坏区、以及桩周表层被动区四部分；分别对应图6所示的桩底压密区（a）、桩端塑性流动区（b）、桩侧摩擦区（c）和桩周塑性流动区（d）。

2.3 桩周土体极限承载力

针对饱和不排水软粘土海床上的圆形桩基础，Skempton给出如下的计算公式［9］

式中：H表示桩基础贯入海床的深度；D表示圆形基础直径；Suavg表示桩底土体抗剪强度平均值；γ′表示基础底部以上土体平均有效容重，Su表示桩土界面平均剪切强度。

在二维条形基础极限承载力计算公式的基础上，Hansen给出如下的计算公式［10］

式中符号同上。

图8 桩腿插桩入泥深度与极限承载力对应关系Fig.8 Relationship between penetration depth and ultimate bearing capacity of jack－up platform

由图8所示桩腿插桩入泥深度与极限承载力对应关系可知，本文基于网格重绘与插值技术（RITSS），通过有限元计算过程中对几何图形进行重绘生成高质量的网格单元，再对单元高斯点处的应力、应变、材料参数进行映射分析，来完成有限元计算过程中动边界造成的非线性问题，从而求得插桩过程中的极限承载能力的方法，计算结果较为合理。

3 结论

本文基于网格重绘与插值技术，在小应变材料本构模型与平衡方程的基础上，较为准确地求解了自升式平台插桩入泥过程的大变形数值问题，并给出了较为合理的土体变形规律与失稳机理。得出如下结论：（1）网格重绘与插值技术（RITSS），对计算平台插桩过程的大变形问题是切实可行的，能够给出较为准确的数值计算结果。（2）本文给出的桩周土体等效塑性应变与桩腿插桩入泥深度间的对应关系，分析了插桩过程桩周土体的压密与剪切过程，较为合理地揭示了桩周土体的变形规律。（3）基于插桩过程中桩周土体的变形规律，本文给出的桩周土体的失稳机理（见图6），在插桩入泥较浅时可以简化为Prandtl失稳模式；随着插桩入泥深度的增加，可以进一步扩展为赞别列夫失稳模式；为进一步深入研究深基础的极限平衡问题奠定了一定的理论基础。

［1］ 罗宏志，蒙占彬.国内深水自升式钻井平台发展概况 ［J］.中国海洋平台，2010，25（4），4－7.

［2］ Jack R L，Hoyle M J R，Hunt R J，et al.Jack－up accident statistics：lots to learn，11th Int Conference，The Jack－up Platform［C］.London：City University，2007.

［3］ SNAME （Society of Naval Architects and Marine Engineers）.Guidelines for site specific assessment of mobile jack－up units［M］.New Jersey：SNAME Technical and Research Bulletin 5－5A，2002.

［4］ SNAME （Society of Naval Architects and Marine Engineers）.Commentaries to guidelines for site specific assessment of mobile jack－up units［M］.New Jersey：SNAME Technical and Research Bulletin 5－5A，2002.

［5］ Baglioni V P，Chow G S，Endley S N，et al.Jack－up foundation stability in stratified soil profiles ［C］.Houston：Proc Offshore Technology Conference，1982.

［6］ HSE （Health and Safety Executive）.Guidelines for jack－up rigs with particular reference for foundation integrity ［R］.Research Report 289，2004.

［7］ White D J，Teh K L，Leung C F，et al.A comparison of the bearing capacity of flat and conical circular foundations on sand ［J］.Géotechnique，2008，58（10），781－792.

［8］ Gemeinhardt J P＇Focht J A.Theoretical and observed performance of mobile rig footings on clay ［C］.The International Society of OTC.The proceedings of Offshore Technology Conference.Houston：The International Society of OTC，1970：549－558.

［9］ Hu Y，Randolph M F.A practical numerical approach for large deformation problems in soil［J］.Int J Num and Anal Methods in Geomech，1998，22（5）：327－350.

［10］ Menzies D，Roper R.Comparison of Jackup rig spudcan penetration methods in clay［C］.The proceedings of 40thOffshore Tech－nology Conference.Houston Texas：The International Society of OTC，2008：19545.