求解一类广义Brouwer不动点问题的连续化方法＊

吕堂红，王 建

（1.长春理工大学理学院，吉林 长春130022；2.中国海洋大学数学科学学院，山东 青岛266100）

0 引言

Brouwer不动点定理在微分方程、数学规划、工程、经济等领域应用广泛［1－3］。1976年，Kellogg等给出了Brouwer不动点定理的构造性证明，从而提出了连续化方法来计算两次连续可微映射Φ（x）的不动点［4］。1978年，Chow等人［5］在有界闭凸集构造了如下同伦

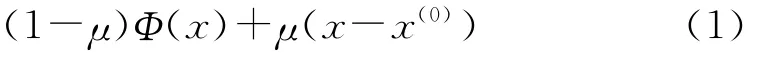
该同伦目前已经成为计算不动点和非线性系统的重要工具［6－8］。

广义Brouwer不动点问题对所在集合没有凸性和有界性要求，所以如何给出该定理的构造性证明并数值求解非凸无界集合上的不动点问题是十分重要的，然而，据所知，在这个领域很少有相应的研究结果.直到最近，人们才把Kamarkar内点法的思想引入到连续化方法中，进而提出了一种新的连续化方法，并处理了一类满足法锥条件的非凸集合上的不动点问题［9－10］。

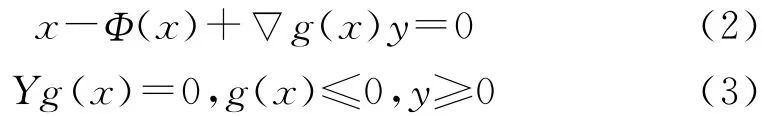
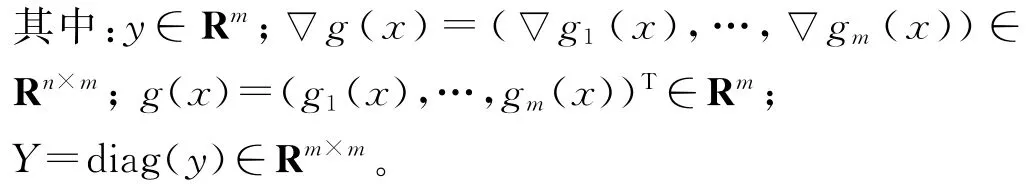
针对系统（2）和（3），文献［9］构造了适当的组合同伦方程，并得到了连续化方法的全局收敛性结果。文献［10］引入二次连续可微映射η（x）∈Rn×m代替梯度g（x），进而把文献［9］的结果推广到了更一般的非凸集合上。

应该指出的是，文献［9－10］的结果都要求Ω是有界的，对于无界非凸区域，目前还没有相应的研究结果出现。本文利用自映射Φ（x）和二次连续可微映射η（x）构造一组无界性条件，在适当的条件下，给出了连接无界非凸区域内部任意给定的点和不动点的同伦路径存在性的构造性证明，从而得到了连续化方法的全局收敛性结果。最后，本文给出了2个数值算例来进一步验证本文结果的有效性。

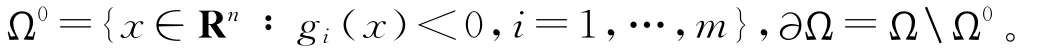
本文需要用到如下符号：Rm＋和Rm＋＋分别代表Rm的非负象限和正象限。另外记x点处的积极集为

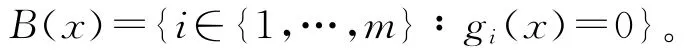
1 理论分析

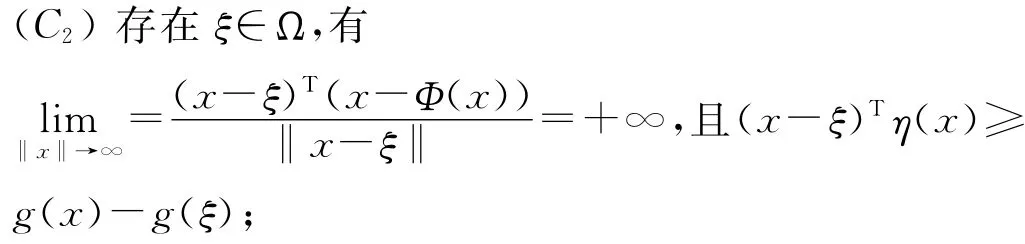
本文的主要工作就是把文献［10］中的Ω有界性去掉，从而使得连续化方法能够在无界非凸集上计算不动点问题，为此本文需做如下假设：（C1）Ω0非空；（C3）对任意给定的x∈ЭΩ，若

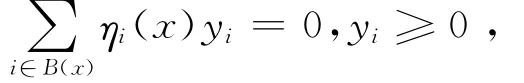
则有yi＝0，i∈B（x）；

（C4）对任意的x∈ЭΩ，则有

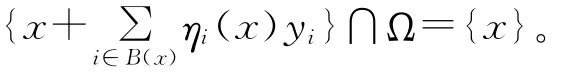
在假设（C1）～（C4）下，为了求解不动点问题，则需要用到同伦方程：H（w，w（0），μ）＝

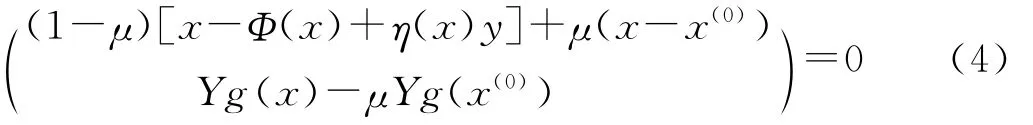
其中：w＝ （x，y）∈Rn＋m，w（0）＝ （x（0），y（0））∈Ω0×

引理1 设 H 如（4）所定义，假设（C1）～（C4）成立。那么对几乎所有的 w（0）∈Ω0×Rm＋＋，0是映射 H（w，w（0），μ）的正则值；H－1（0）所含曲线是光滑的，其中有一条起始于（w（0），1），记作Γw（0）。

公司层面的控制是指存在于公司整体层面，对业务层面实施的控制措施产生普遍、深远影响的控制，体现公司的风险管理理念、风险承受能力、公司治理监控水平、对道德价值观的遵守、人员素质与发展水平以及职责权力分工。根据《企业本部控制基本规范》，公司层面控制的主要内容包括内部环境、风险评估、信息与沟通及内部监督四个部分，其基本要求主要体现在企业体制、机制、规章、制度等方面。

根据引理1，则知同伦曲线是存在的，下面主要证明同伦曲线的有界性。令

Ω＋（ξ）＝｛x∈Ω∶（x－ξ）T（x－ξ）T（x－Φ（x））＞0｝，Ω－（ξ）＝Ω＼Ω＋（ξ）。

引理2 设 H 如（4）所定义，假设（C1）～（C4）成立。那么对几乎所有的 w（0）∈Ω0×Rm＋＋，如果0是映射H（w，w（0），μ）的正则值，那么w 的分量x 是有界的。证明 容易证明如下不等式成立：

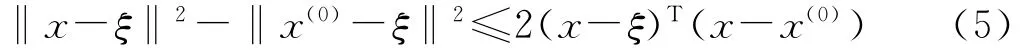
若结论不成立，则存在同伦路径上的点列｛（x（k），y（k），μk）｝使得当

根据假设（C4），则存在常数C使得

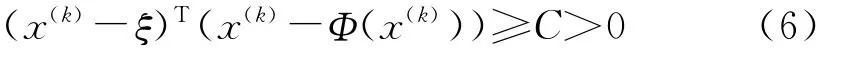
当x（k）∈Ω－（ξ）时，由（6）式，则情形不会发生。又Ω＝Ω－（ξ）∪Ω＋（ξ），因此下面只须证明w的x分量在Ω＋（ξ）内也是有界的。

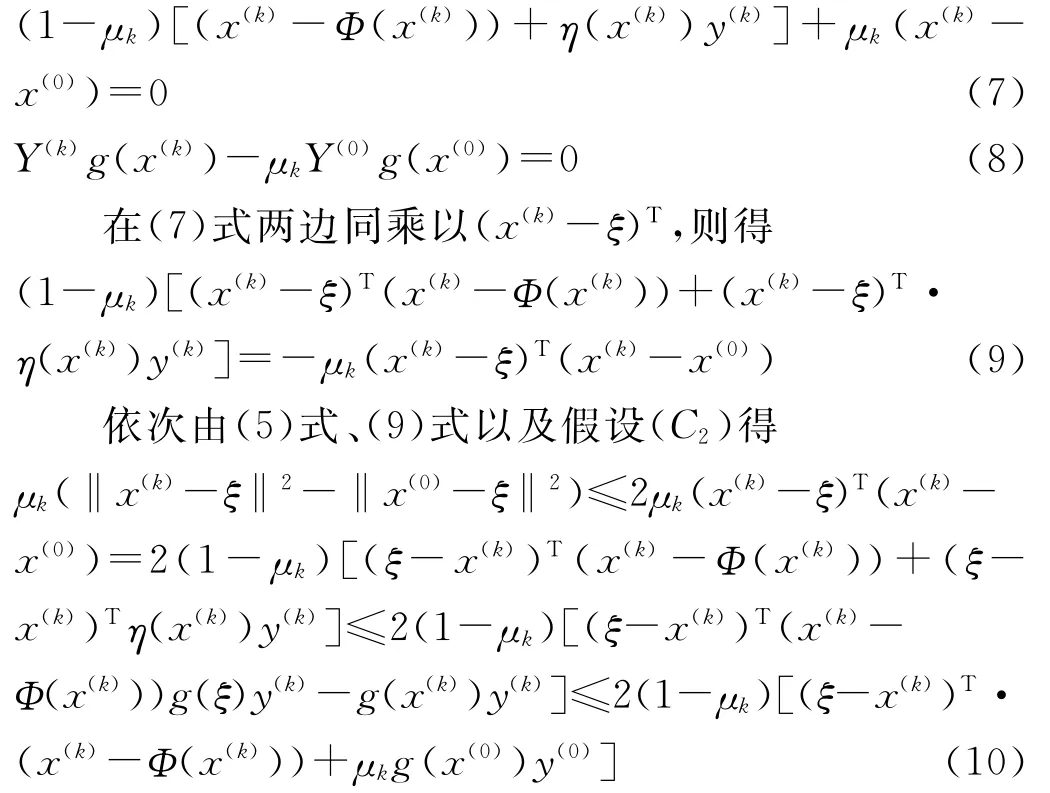
再由（10）式得

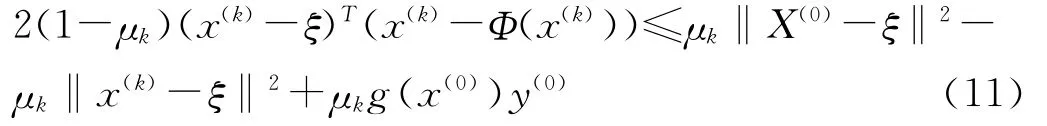
当x（k）∈Ω＋（ξ）时，若‖x（k）‖→∞，因为‖x（0）－ξ‖2是常量，且μk∈（0，1］，那么存在充分大的k使得‖x（k）－ξ‖＞M，从而（11）式的左边严格大于0，而（11）式的右边严格小于0，矛盾。因此w的x分量在Ω＋（ξ）内也是有界的，证明完毕。

下面给出连续化方法的全局收敛性结果。

定理1 设 H 如（4）所定义，假设（C1）～（C4）成立。那么对几乎所有的，同伦方程（4）产生一条始于（w（0），1）的光滑曲线Γw（0），并且当μ→0时，Γw（0）的极限集T×｛0｝Ω××｛0｝是非空的，且T中的每一点（x＊，y＊）的分量x＊都是Φ（x）的不动点。证明 容 易 证 明 DH （w，w（0），μ ） ＝行满秩的，从而0是H（w，w（0），μ）的正则值。根据参数化Sard定理，对几乎所有的w（0），0是映射 Hw（0）∶Ω×Rm＋×（0，1］→Rn＋m的正则值。再由逆象定理，H－1w（0）（0）由一些光滑曲线组成。因为 Hw（0）（w（0），1）＝0，那么存在1维的C1曲线（w（s），μ（s））（记作Γw（0））使得H（w，w（0），μ）＝0，（w（0），μ（0））＝（w（0），1）。

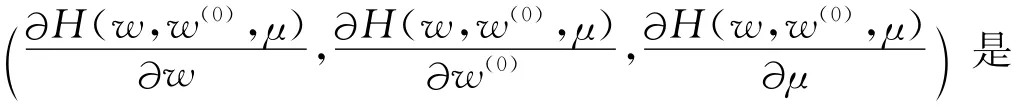
根据一维流形分类定理，Γw（0）或者微分同胚于单位圆或者微分同胚于单位区间。容易证明ЭHw（0）（w（0），1）／Эw 是非奇异的，因此Γw（0）微分同胚于单位区间。

设（w＊，μ＊）是Γw（0）上的极限点，那么下列情形可能发生：

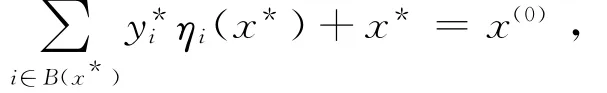
（ii）若μ＊＜1，当k→∞时，因为有界的，那么（12）式的右边是有界的，而（12）式的左边趋于无穷，矛盾。

根据上面的讨论，则知只有情形（a）发生，因此根据不动点问题的等价系统（2）和（3），x＊是映射Φ（x）的不动点。证明完毕。

2 数值实验

由定理1知，几乎对所有的w（0）∈Ω0×Rm＋＋，同伦方程（4）产生一条光滑曲线Γw（0），此曲线称为同伦路径，从（w（0），1）出发数值跟踪Γw（0），直到μ→0，就能得到系统（2）和（3）的一个解。

通过对 H（w（s），w（0），μ（s））＝0，（s是弧长参数）求微分，得到下面的定理2。

定理2 同伦路径Γw（0）是由下面的常微分方程的初值问题确定

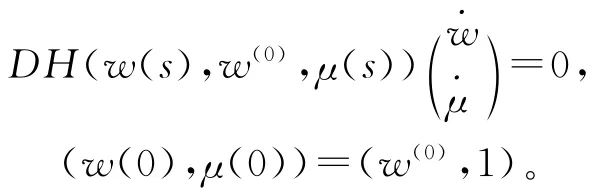
至于如何跟踪同伦路径，现在已经有很多算法，可以参考文献［11］。

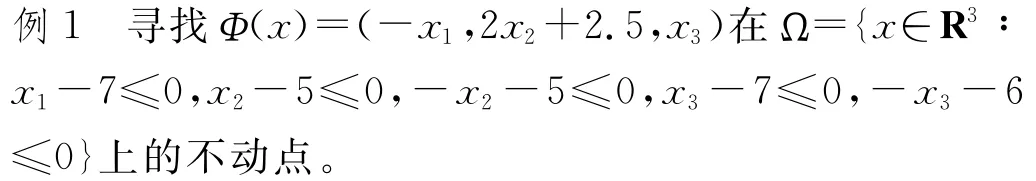
容易验证Ω无界且满足假设（C1）～（C4）在本例中，选择3个初始点x（0）1＝（3，－1，3），x（0）2＝（－3.5，2，3）以及x（0）3＝（2.5，4，5）。利用预估－校正算法，沿着3条不同的解曲线，可以跟踪到Φ（x）的不动点

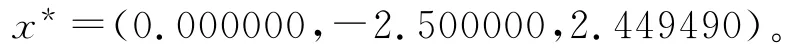
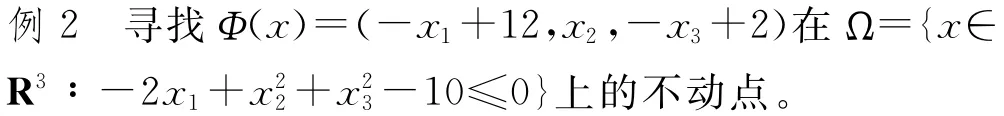
容易验证Ω无界且满足假设（C1）～（C4）。在本例中，选择3个初始点x（0）4＝（12，－1，3）－1，13）以及x（0）6＝（12，－1，－3）。利用预估－校正算法，沿着3条不同的解曲线，可以跟踪到Φ（x）的不动点

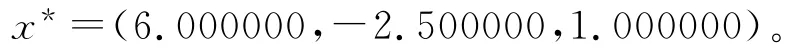
3 结语

已有的研究结果主要利用连续化方法求解无界凸集上的不动点问题。本文提出了一组无界性条件，从而使得连续化方法能够处理一类无界非凸集合上的不动点问题，在较大程度上推广了已有的研究结果。数值实验表明本文的研究结果是有效的。由于不动点问题在微分方程领域起着重要作用，所以本文作者准备在未来的研究中把本文的研究结果推广到微分方程领域，进而得到一些有意义的研究结果。

［1］ Garcia C B，Zangwill W I.Pathways to Solutions，Fixed points and equilibria［M］.New Jersey：Prentice－Hall，1981.

［2］ Bollobas B，Fulton W，Katok A，et al.Fixed Point Theory and applications［M］.London：Cambridge University Press，2004.

［3］ Heikkila S，Reffett K.Fixed point theorems and their applications to theory of Nash equilibria［J］.Nonlinear Anal Theory Methods Appl，2006，64：1415－1436.

［4］ Kellogg R B，Li T Y，Yorke J A.A constructive proof of the Brouwer fixed－point theorem and computational results［J］.SIAM J Numer Anal，1976，13：473－483.

［5］ Chow S N，Mallet－Paret J，Yorke J A.Finding zeros of maps：homotopy methods that are constructive with probability one ［J］.Math Comput，1978，32：887－899.

［6］ Garcia C B，Zangwill W I.An approach to homotopy and degree theory［J］.Math Oper Res，1979，4：390－405.

［7］ Watson L T，Scott M R.Solving spline－collocation approximations to nonlinear two－point boundary value problems by a homotopy method［J］.Appl Math Comput，1987，24：333－357.

［8］ Li Yong，Lin Zhenghua.A constructive proof of the Poincar Birkhoff theorem ［J］.Trans Amer Math Soc，1995，347：2111－2126.

［9］ Yu Bo，Lin Zhenghua.Homotopy method for a class of nonconvex Brouwer fixed－point problems ［J］.Appl Math Comput，1996，74：65－77.

［10］ Lin Zhenghua，Yu Bo，Zhu Daoli.A continuation method for solving fixed points of self－mappings in general nonconvex sets［J］.Nonlinear Analysis，2003，52：905－915.

［11］ Allgower E L，Georg K.Introduction to numerical continuation methods［M］.Philadelphia：SIAM Society for Industried and Applied Mathematics，2003.