一种粒子概率假设密度的模糊关联方法＊

王 品，谢维信，刘宗香，高存臣

（1.深圳大学ATR国防科技重点实验室，广东 深圳518060；2.中国海洋大学数学科学学院，山东 青岛266100）

多目标跟踪技术一直是目标跟踪领域的一个热点研究问题。目标数目不定的多目标跟踪问题无论在理论上还是在应用中都是具有挑战性的问题。传统的多目标跟踪方法是先关联后估计，关联精度直接影响跟踪效果，目标数未知并且存在杂波和虚警时，关联很难实现［1－4］。Mahler等从统计的角度提出了多目标情况下“一阶矩滤波器”的概念（也称概率假设密度滤波器，PHDF）［4］，PHDF避免了观测值和状态值之间直接关联，但迭代过程中存在集合积分运算，计算上难以处理。所以 Vo等提出粒子 PHDF［5］（PF－PHDF），PFPHDF可以很好的估计出每个时刻多目标的状态值［6］，但PF－PHDF跟踪结果不能确认每个目标的状态，进而不能给出有效的跟踪航迹。Panta提出多假设关联算法和PF－PHD滤波结合的跟踪方法［6］，但用多假设关联算法过多地依赖目标和杂波的先验知识并且计算复杂很难实时实现［6－7］。近年来Vo等又提出了适用于线性高斯系统的高斯混合PHD滤波方法（GMPHD）［8］，推导了PHD的解析表达式，继而又有大量改进的 GM－PHD滤波方法［9－11］，对于系统噪声和量测噪声为非高斯噪声的多目标跟踪环境GM－PHD就无法使用，但PF－PHD仍然适用。

针对以上问题，提出1种新的基于PF－PHDF的多目标模糊跟踪方法，这种方法用粒子滤波预测和更新多目标状态集合的PHD，估计出目标数并用模糊C－均值聚类算法给出多目标的状态估计，把得到的目标状态作为新的观测集，然后用模糊关联得到各个航迹的关联结果，最后通过建立临时航迹滤掉了杂波点并且有效的提高了目标的跟踪精度。

1 基于随机有限集的多目标跟踪框架

1.1 多目标跟踪模型

在多目标跟踪系统中，目标的出现和消失都是随机的。本文假设每一时刻出现的新目标数服从均值为λa的柏松分布。一个k时刻的目标下一时刻可能存在也可能消失，假设目标从k－1时刻存活到k时刻的概率是ek｜k－1，则目标在k时刻的死亡概率为1－ek｜k－1。目标的检测概率为PD。

目标的运动服从马尔可夫动态模型：

观测表示为：

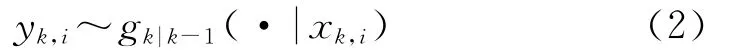
假设在k时刻，目标数和观测数分别为Nk和Mk，多目标的状态集与观测集分别表示随机有限集合的形式，即Xk＝｛xk，1，…xk，Nk｝Es为多目标状态，Zk＝｛zk，1，…zk，Mk｝Eo为多目标观测，其中Es，Eo分别表示状态空间和观测空间。若k－1时刻状态集为Xk－1，则k时刻的状态集可以表示为：

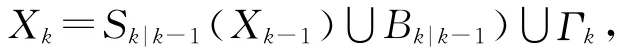
其中：Sk｜k－1（Xk－1）表 示 k 时 刻 仍 存 活 的 目 标 集；Bk｜k－1（Xk－1）表示由k－1时刻衍生的目标集；Γk表示k时刻出现的新目标集。一般用f（Xk｜Xk－1）表示多目标的状态转移密度。类似地，k时刻的观测集可表示为：Zk＝Gk（Xk）∪Ck（Xk），其中Gk（Xk）表示由 Xk产生的观测值随机有限集；Ck（Xk）表示杂波或者虚警产生的随机有限集。

1.2 随机有限集的概率假设密度滤波

随机有限集理论的引入为多目标的Bayes滤波提供了与单目标的Bayes滤波一致的完美形式，但需要建立相应的概率分布和概率密度的概念。由于涉及到计算集导数和广义积分问题，在随机有限集理论中概率分布一般采用信任函数的形式，即：对于随机有限集Ξ的概率分布表示为［5］：

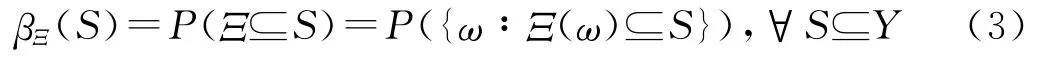
1.2.1 多目标Bayes滤波 假设k－1时刻多目标的全局后验密度为pk－1（Xk－1｜Z1∶k－1），则k时刻多目标全局密度预测方程为［4］：

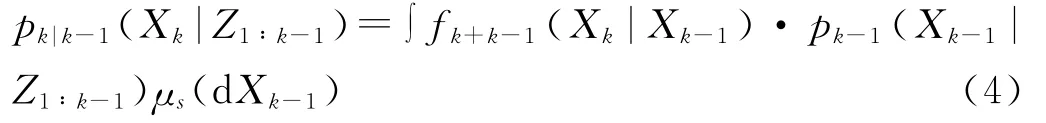
其中：μs表示一种合适的测度［5］。更新后得到k时刻多目标的全局后验密度：

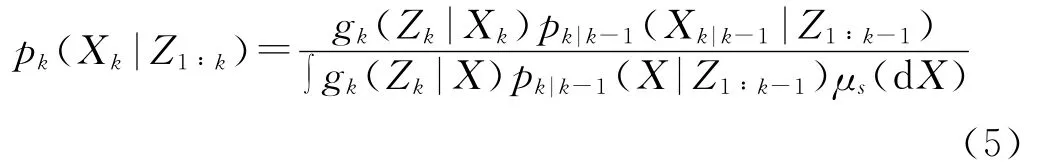
在目标数目不定或数目较大的情况下全局密度的计算非常困难，使得基于全局密度的多目标Bayes滤波在工程上难以实现。所以Mahler等从统计的角度提出了多目标情况下“一阶矩密度”的概念，即概率假设密度。

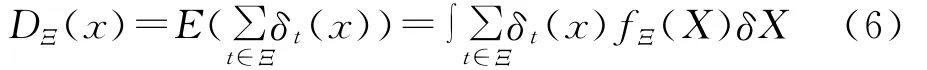
其中：δx表示中心为x 的 Dirac delta函数；DΞ（x0）是在x0点期望的目标密度；∫SDΞ（x）dx时出现在S内的期望的目标数，而利用DΞ（x）的极值可以给出目标的状态估计。

PHD滤波器（PHDF）就是对多目标后验密度的概率假设密度Dk｜k递推过程，也是通过预测更新2个步骤来实现。假设k－1时刻后验密度为υk－1。

PHD预测方程：

PHD更新方程：

1.2.2 概率假设密度 随机有限集Ξ的概率假设密度表示为：

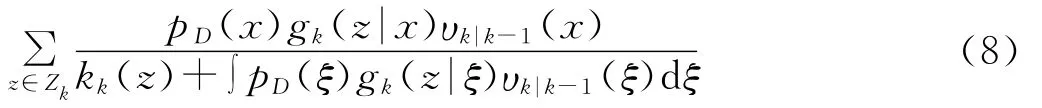
其中：ek｜k－1，fk｜k－1，pD，gk｜k－1同前定义；βk｜k－1，βk分 别表示Bk｜－1，Bk的PHD；kk表示杂波的PHD。PHD滤波一般通过粒子滤波（SMC）来实现，粒子的更新权值之和等于估计的目标数。

2 基于随机有限集和模糊关联的多目标跟踪

2.1 模糊关联

模糊关联（FDA）算法是以模糊均值聚类（FCM）算法为基础的，FDA的目的就是把每条航迹的预测值vi（i＝1，2…c）作为聚类中心，然后利用FCM方法把每个观测和可能航迹之一关联起来。FCM是一种能自动对数据样本分类的方法。他通过优化模糊目标函数得到每个样本点相对类中心的隶属度，从而决定样本点的归属。即：找出最佳隶属度uik和最佳模糊聚类中

PF－PHDF虽然能给出在当前时刻目标的估计状态，但是它没有保留任何目标航迹。然而有些数据关联算法可以基于PF－PHDF给出目标的跟踪航迹，因此，需要结合数据关联算法来获得目标的航迹，将模糊数据关联算法引入到PHDF方法当中对复杂情况下多目标进行跟踪。具体过程见图1。

由图1可已看出：由k时刻的观测值通过PFPHD得到每个粒子的状态、权值、和目标数，并通过模糊聚类（FCM）得到每个目标k时刻的估计状态，然后根据模糊关联（FAD）得到多目标跟踪航迹，最后通过建立临时航迹的方法确定形成多目标航迹。

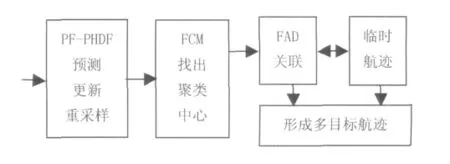
图1 PF－PHDF与模糊关联跟踪实现过程Fig.1 Tracking with the PF－PHDF and fuzzy associate

2.2 算法的具体实现步骤如下：

步骤一 初始化PHD，即：Dk｜k。在k＝0时刻，用带权重的粒子初始化概率假设密度D0｜0，即：初始密度函数为初始的粒子个数。

PF－PHD的具体过程是：

步骤四 模糊关联的具体实现步骤：

（2）利用FCM算法求分割矩阵U，分割矩阵中的元素uik代表航迹i和观测k之间的关联度量，分割矩阵包含了所有航迹和所有观测的隶属度。相似性度量由下式确定

（3）对最大隶属度值uMik进行搜索，将观测kM赋给航迹iM，然后把uMik对应的行和列上的值赋值为0。重复搜索一直到所有观测或者所有航迹有关联对象，或者当时的最大隶属度小于隶属度初始阈值。

步骤五 判断临时航迹内是否为空，如果临时航迹内有航迹，接下来就和临时航迹内的航迹关联，转到步骤四。然后分析关联不上的航迹和观测，即找出所有没有关联上的航迹和没有关联上的观测，没有关联上的观测形成新的航迹，没有关联上的航迹暂时保留在临时航迹内。

步骤六 确认目标，分离并剔除杂波。被保留的航迹连续3个时刻都没有相应的观测与之关联，认为该目标在第一次没有关联对象的时候已经消失或离开观测区域。

3 仿真实验

为了验证算法的性能，便于比较，仿真实验条件如同文献［6］，实验步长为50。传感器的观测空间为二维平面区域S＝［－400，400］×［－400，400］，时间间隔T＝1s，PD＝0.99，ek｜k－1＝0.95，λa＝3。

每个目标的运动模型和观测模型分别为：

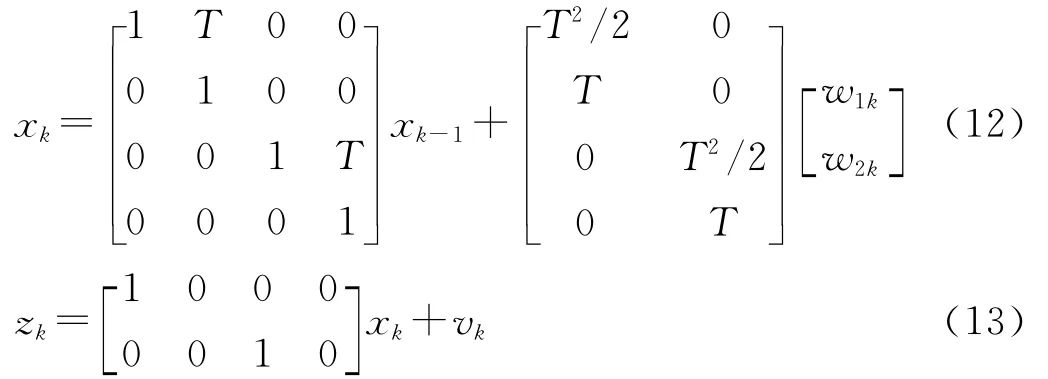
w1k，w2k，vk都是均值为0的高斯白噪声，标准差分别为1、0.1和0.5。初始粒子数为1 000，每个目标分配的粒子数目为500。多目标估计误差用Wasserstein距离［5］。仿真结果见图2～3。

图2和3显示了50s内PF－PHD方法跟踪真实轨迹的估计值，从图中可以看出，PF－PHDF的跟踪结果只是每个时刻目标的状态的估计值，没有跟踪轨迹，而且偶尔估计误差比较大，有的杂波点没有去掉，这是因为只利用聚类技术估计的状态值具有不可靠性［8］。

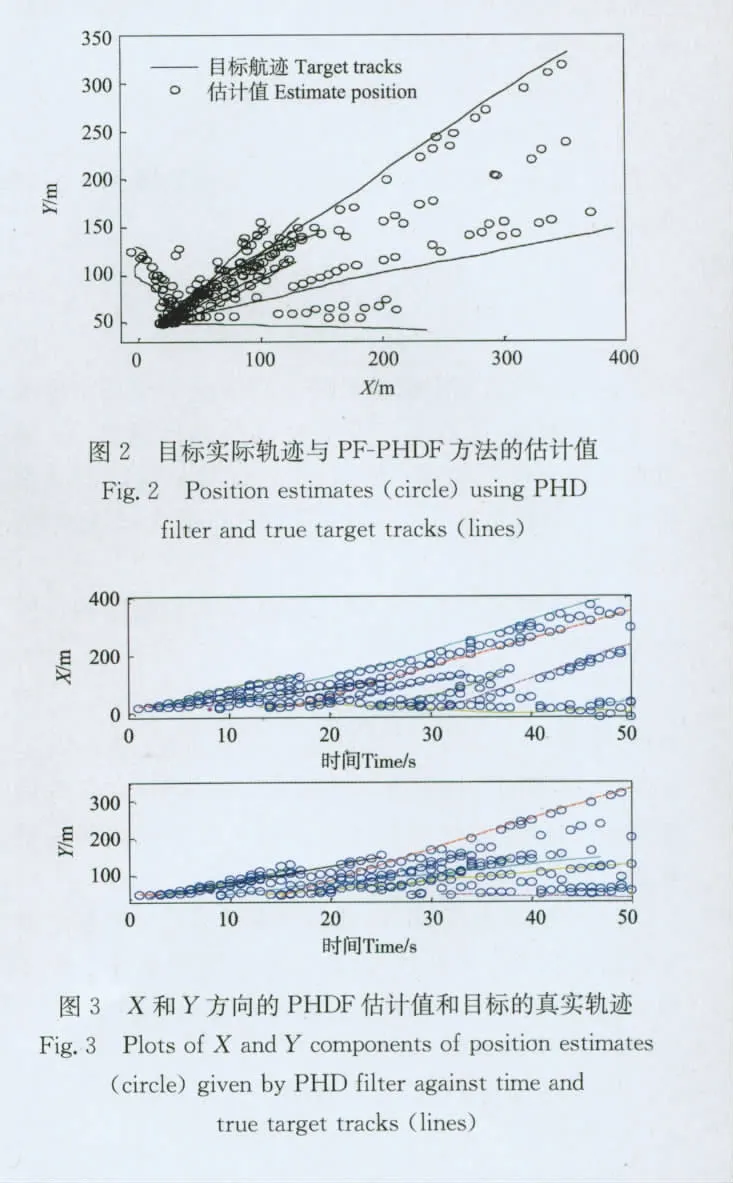
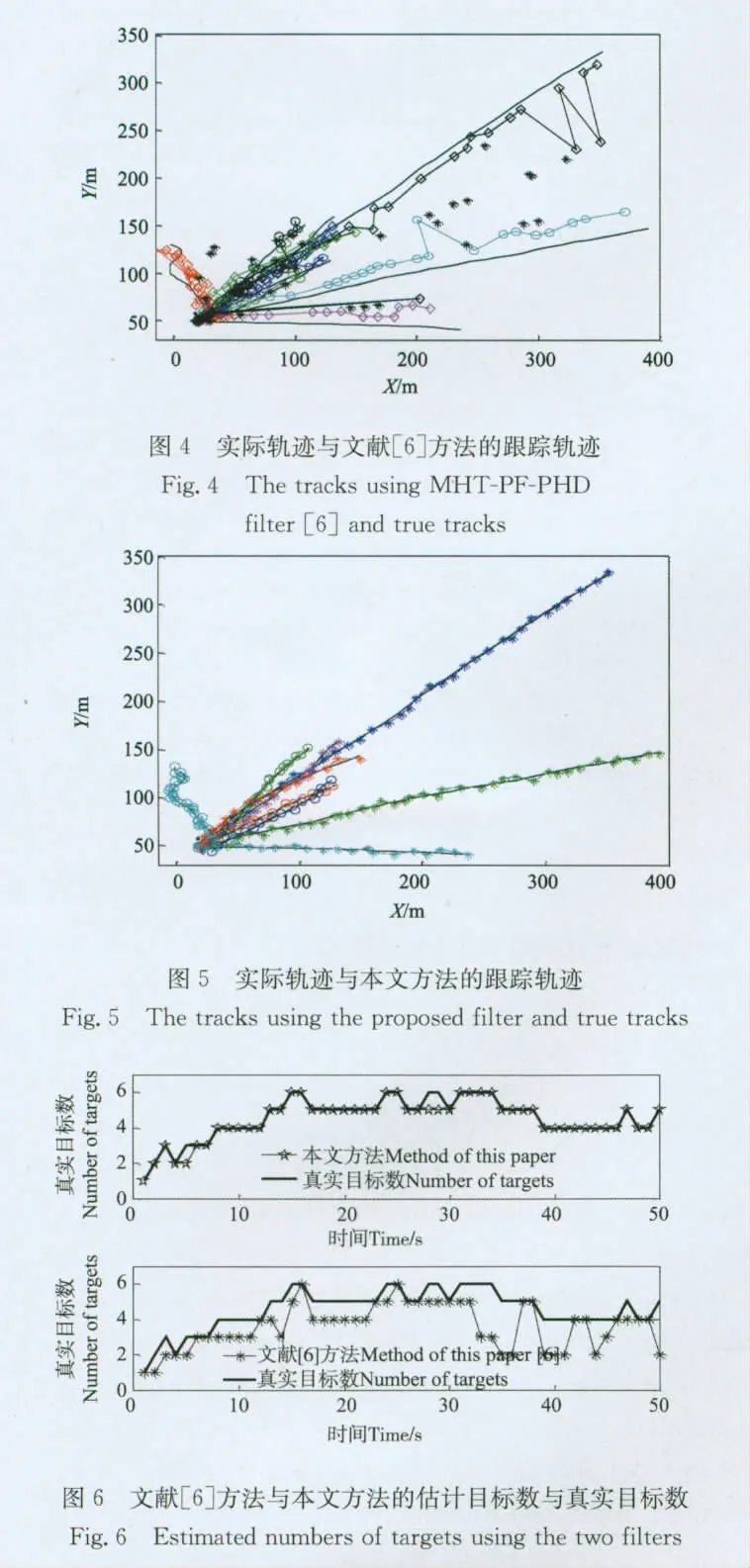
图4是经过PF－PHDF滤波后，然后利用多假设关联的方法给出多个目标的运动轨迹，但是无法分辨出杂波点，而且通常目标的轨迹也不连续，这是由于漏检或者是PHDF滤波过程中滤掉了真实目标点。图5是本文提出方法的跟踪航迹，可以看出本文方法明确了给出了每个目标的运动轨迹，由于保留临时航迹思想的引入，滤除了杂波点并修复了漏检等情况造成的目标轨迹的中断。图6是2种方法跟踪目标数的比较，文献［6］的估计目标数中作者首先去掉了每个时刻的杂波点数，也就是2种发放估计的真实目标数的比较，明显看出本文方法能比较准确的估计出目标数。图7是文献［6］方法和本文方法的跟踪误差比较，从图中可以看出，本文方法的状态估计误差明显小于文献［6］的方法，进一步表明了本文方法的优越性。

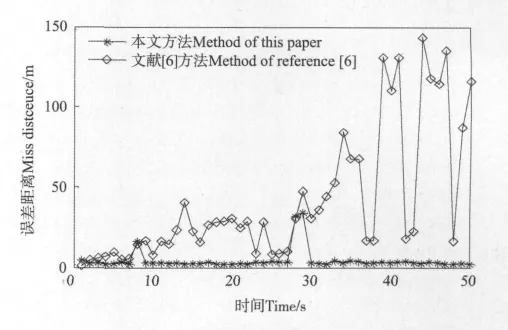
图7 本文方法和文献［6］方法的状态估计误差比较Fig.7 Wasserstein distance between point estimate outputs of MHT－PHD filter［6］and the proposed filter

表1给出了3种PHD滤波器的时间复杂度的对比结果，从表中看出，PF－PHD的实时性能最好，实时性能最差，而 FDA－PF－PHD 实时性能比 MHT－PFPHD要好。这是因为每次关联MHT的计算量比FDA的计算量大。总体看来本文提出的方法的跟踪精度较高，跟踪速度相对较快。

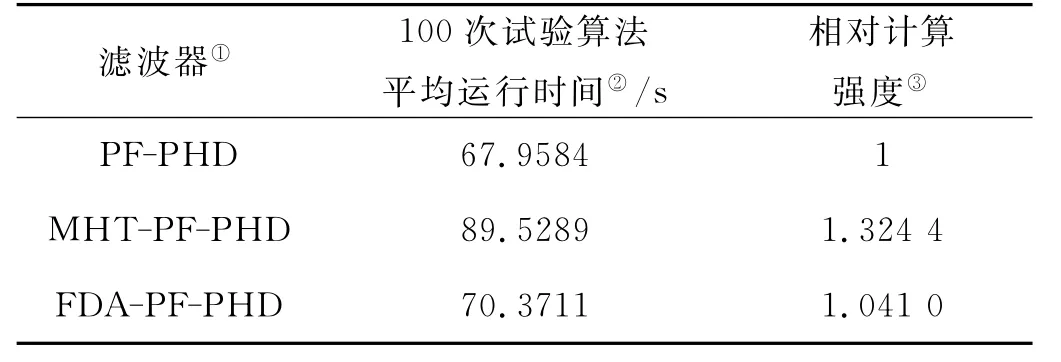
表1 CPU运行时间对比Table 1 Comparison of CPU running time

4 结语

目标数目不定的多目标跟踪问题无论在理论上还是在应用中都是具有挑战性的问题。本文利用随机集的概率假设密度滤波的方法确定目标数目并估计出每个时刻的目标状态，然后利用模糊数据关联的方法给出各个目标的运动轨迹，同时提出了建立临时航迹的方法。通过大量的仿真实验与文献算法的跟踪性能进行比较，实验结果表明，新算法有效地避免漏检造成的目标丢失，得到每个目标的航迹。特别对于目标发生交叉的情况，能很好地区分每个目标的航迹，并能很好的去除杂波点。CPU耗时比文献［6］的方法减少了20℅。下一步将继续研究优化算法，进一步提高多目标跟踪的实时性，另外考虑研究PHDF的收敛性和稳定性［13－15］，进一步提高 PHD在多目标跟踪领域的实用性。

［1］ 徐晓滨，文成林，刘荣利.基于随机集理论的多源信息统一表示与建模方法 ［J］.电子学报，2008，36（6）：1174－1181.

［2］ Mahler R.Random sets：unification and computation for information fusion－a retrospective assessment［C］.the 7th International Conference on Information Fusion，Sweden：ICIF，2004：1－20.

［3］ Chenglin Wen，Zhiliang Li，Xiaobin Xu.A new method for extracting fuzzy evidence from fuzzy information based on the random set theory ［C］.Chongqing：7th World Congress on Intelligent Control and Automation，2008：4999－5003.

［4］ Mahler R.Statistical multisource－multitarget information fusion［M］.Boston：Artech House Publishers，2007.

［5］ Vo B，Singh S，Doucet A.Sequential monte carlo methods for multi－target filtering with random finite sets ［J］.IEEE Trans Aerospace and Electronic Systems，2005，41（4）：1224－1245.

［6］ Panta K，Vo B，Singh S.Novel data association technique for the probability hypothesis density filter ［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43（2）：556－570.

［7］ Papi F，Battistelli G，Chisci L，et al.Multitarget tracking via joint PHD filtering and multiscan association［C］.Seattle：the 12th International Conference on Information Fusion，2009：1163－1170.

［8］ Ba－Ngu Vo，Wing－Kin Ma.The Gaussian mixture probability hypothesis density filter［J］.IEEE Trans.Signal Processing，2006，54（11）：4091－4104.

［9］ Clark D，Vo B T，Vo B N，et al.Gaussian Mixture Implementations of Probability Hypothesis Density Filters for Non－linear Dynamical Models［C］.The IET Seminar on Target tracking and Data Fusion：Algorithms and Applications.Birmingham，UK：IET Press，2008：21－28.

［10］ Clark D，Vo B T，Vo B N，et al.Gaussian Particle Implementations of Probability Hypothesis Density Filters［C］.IEEE Aerospace Conference.Montana，USA：AIAA Press，2007：1－11.

［11］ 张俊根，姬红兵，蔡绍晓.基于高斯粒子JPDA滤波的多目标跟踪算法 ［J］.电子与信息学报，2010，32（11）：2686－2690.

［12］ Mahler R.PHD filters of higher order in target number［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43（3）：1523－1543.

［13］ 高存臣，徐伟丽.一类线性中立型不确定时滞系统的鲁棒稳定性［J］.中国海洋大学学报：自然科学版，2010，40（7）：155－158.

［14］ Clark D，Bell J.Convergence results for the particle PHD filter［J］.IEEE Trans Signal Processing，2006，54（7）：2652－2661.