上海地区雷电流幅值分布特征分析

2012-10-15司文荣张锦秀顾承昱

电力与能源 2012年2期

司文荣，张锦秀，顾承昱，郑旭

（1.上海市电力公司电力科学研究院，上海 200437；2.上海市电力公司，上海 200122）

0 引言

目前开展的实际雷电活动下的线路雷击跳闸率计算，以雷电日和落雷密度为参数的输电线路雷击跳闸率计算的对比分析以及基于雷电定位系统的雷电流幅值统计分析等［1］，其主题就是欲根据不同地区实际的落雷分布情况以及参数特征，寻找方法和途径，对输电线路防雷设计起指导作用［2］。但是，大多数的研究结果，只依据了几年的累积数据，要得出可信度较高的雷电参数统计数据一般需要10年的数据积累。因为雷电活动与太阳黑子有关，太阳黑子的活动周期约为10年。此外，雷电流幅值概率作为雷击闪络计算的参数之一去取值，其精确性直接关系到雷击闪络率的计算精确性［3］。因此，找出相对精确的雷电流幅值概率计算公式十分必要。

我国大多数省市目前均已建立雷电定位系统，并且积累了多年的数据，在确定雷击故障点的位置方面发挥了很好的作用，受到运行调度和安监等部门的欢迎。但在雷电参数统计方面的应用开拓较少，需要进一步发挥该系统在雷电参数测量方面的作用，以制订各地区的雷电参数，改进防雷保护措施。

本文基于上海电网雷电定位系统积累的2001年至2010年的落雷数据，对上海市整体区域以及所属11个子区域的正极性、负极性及综合雷电流幅值的累积概率分布和均值分布变化规律进行统计和描述。

1 数据来源和处理方法

上海地区雷电定位系统［4］目前由8个雷电探测站组成，地理位置分布如图1所示。雷电监测系统基本覆盖了上海市11个主要行政区域，是一套全自动、大面积、高精度、实时的雷电监测系统。该系统采用遥测法，依据M.A.Uman提出的地闪回击场模型得到雷电流幅值数据，并对监测获取的落雷电流峰值采用统一的雷电流幅值归一化（100km）修正模型。在给出上海地区落雷电流幅值分布前，对目前已有的国内电力相关标准、IEEE导则及CIGRE推荐的雷电流幅值分布计算式进行介绍和认识。

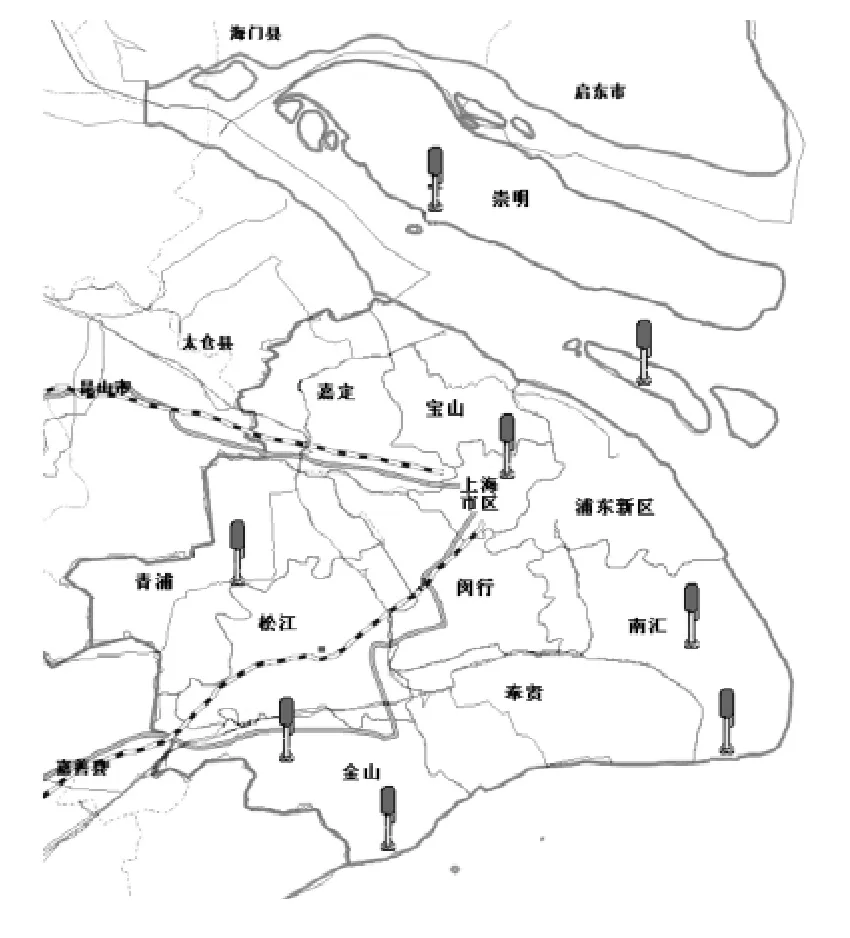
图1 上海地区雷电定位系统探测站分布

2 推荐的雷电流幅值分布计算式

在雷电定位系统出现之前，国内对雷电的基本参数研究较少，一些工程设计的防雷计算公式来自于国外。例如：1962—1987年在浙江新杭线安装钢棒进行线路雷击测量研究，共测得703次雷击数据，得到了25年雷电流幅值拟合式lgPI＝－I／87.6。1997年我国电力行业标准《交流电气装置的过电压保护和绝缘配合》（DL／T 620—1997）即采用了这次结果，将雷电流幅值概率取为lgPI＝－I／88.0。

早在1977年，Pobolansky根据欧洲、澳洲和美国对雷击的观测结果，提出用PI＝（1＋（I／25）2.0）－1计算雷电流幅值概率。以后的研究者根据不同地区的观测，也提出了不同的计算公式，如Eriksson和Anderson提出用PI＝（1＋（I／31）2.6）－1计算雷电流幅值概率，并被IEEE Std推荐使用。还有一些类似的计算式，只是其中参数取值不同，如CIGRE推荐用PI＝（1＋（I／12）2.7）－1计算雷电流幅值概率。而算式中的参数25，31，12是反映中值电流；参数2.0，2.6，2.7是陡度系数。以中值电流25为例，大于25kA电流的概率为50%，陡度系数为2.0，反映的是该概率曲线的陡度，数值越大，表明概率曲线变化越快或越陡，参见图2中的CIGRE概率曲线。反之，数值越小则表明此概率曲线越平缓，参见图2中的国内标准概率曲线。

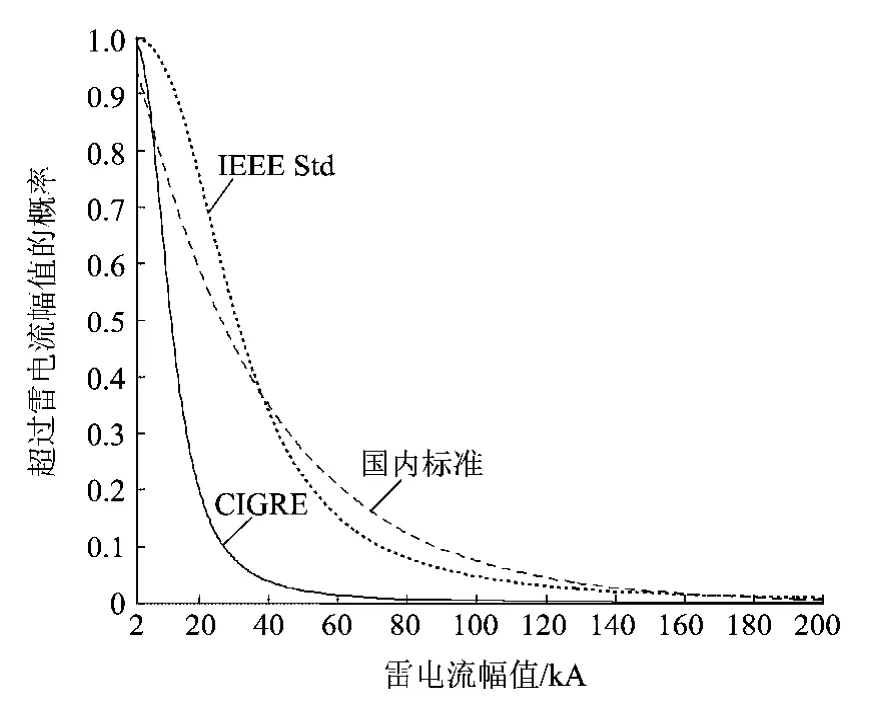
图2 推荐的雷电流幅值概率分布

由f（I）＝（1－PI）′，电流取值为2kA≤I≤200kA，可以求得图2对应的各幅值累积概率密度分布［5］，如图3所示。

图3 对应图2的雷电流幅值概率密度分布

3 上海市整体区域的雷电流幅值分布统计

3.1 雷电流幅值累积概率分布

采用IEEE推荐的PI＝（1＋（I／I＇）α）－1雷电流幅值概率计算式，统计的上海市2001—2010年整体区域雷电流幅值分布参数，如表1所示。

表1 上海市整体区域的雷电流幅值分布参数

在2001—2010年中，雷电流幅值分布参数变化较大，其中正极性雷电流幅值分布中值参数变化区间为［17.3，68.5］，其陡度系数的变化区间为［1.4，3.5］；而负极性雷电流幅值分布中值参数变化区间为［16.8，42.1］，其陡度系数的变化区间为［2.0，3.1］，体现了雷电活动随着年份的变化，具有一定的随机性。图4对上海市整体区域2001—2010年数据的雷电流幅值累积概率分布给予示例。其中，负极性幅值分布的中值电流为26.669kA，陡度参数为2.344，与IEEE Std推荐算式的参数较接近。正极性幅值分布的中值电流为23.669kA，与负极性分布的中值电流相差不大，但陡度系数较小，仅为1.520。

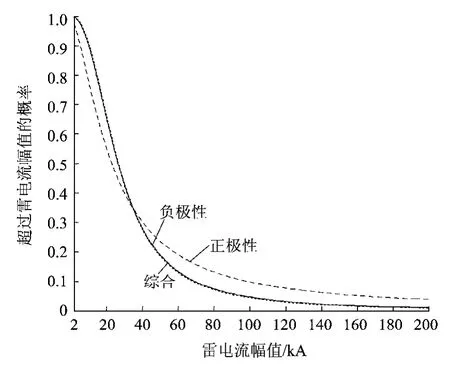
图4 2001—2010年的雷电流幅值累积概率分布

正、负极性10年落雷数据综合统计后分布的中值电流为26.562kA，陡度系数为2.302，与负极性分布的两个参数几乎一致，这是由于正极性雷击次数相对于负极性雷次数来说很小引起的。

由f（I）＝（1－PI）′和表1数据，可得10年落雷数据正、负极性雷电流幅值的概率密度计算公式分别为式（1）、式（2）和图5所示（综合的计算公式这里不再给出，仅在图5中给出曲线）：

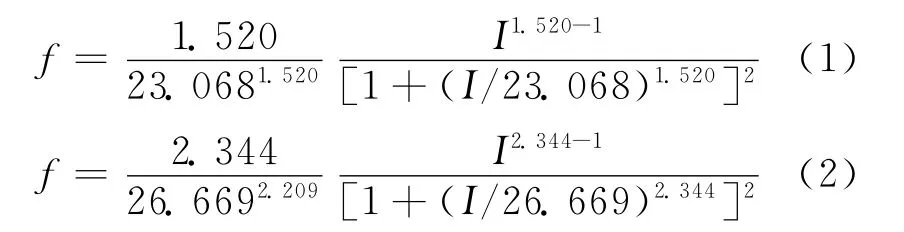
可以看出，正、负极性雷电流幅值的概率密度分布相差较远。

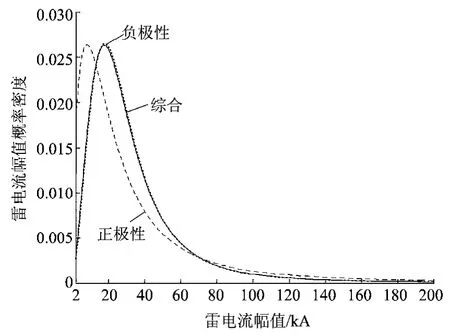
图5 对应图4的雷电流幅值概率密度分布

3.2 雷电流平均幅值

图6 为上海市整体区域正、负极性及综合雷电流平均幅值随年份变化的曲线。

图6 上海市整体区域10年的雷电流平均幅值

由图6可以看出，正极性的雷电流平均幅值均大于负极性的雷电流平均幅值。剔除2001年和2002年两个异常数据后，正、负极性雷电流平均幅值随年份变化存在弱相关性，随机性大，其中正极性雷电流平均幅值的中值电流为39.4kA，标准偏差为6.15kA，而负极性雷电流平均幅值的中值电流为32.0kA，标准偏差为6.39kA。此外，综合雷电流平均幅值与负极性随年份变化的分布曲线几乎一致，这同样是由于正极性雷击次数相对于负极性雷击次数来说很小引起的。

4 上海市各行政区域的雷电流幅值分布统计

表2给出了上海市各行政区域2001—2010年落雷数据，依据PI＝（1＋（I／I＇）α）－1统计获取的正、负极性雷电流幅值分布参数，综合雷电流幅值统计的参数与负极性的参数相近，不再给出。

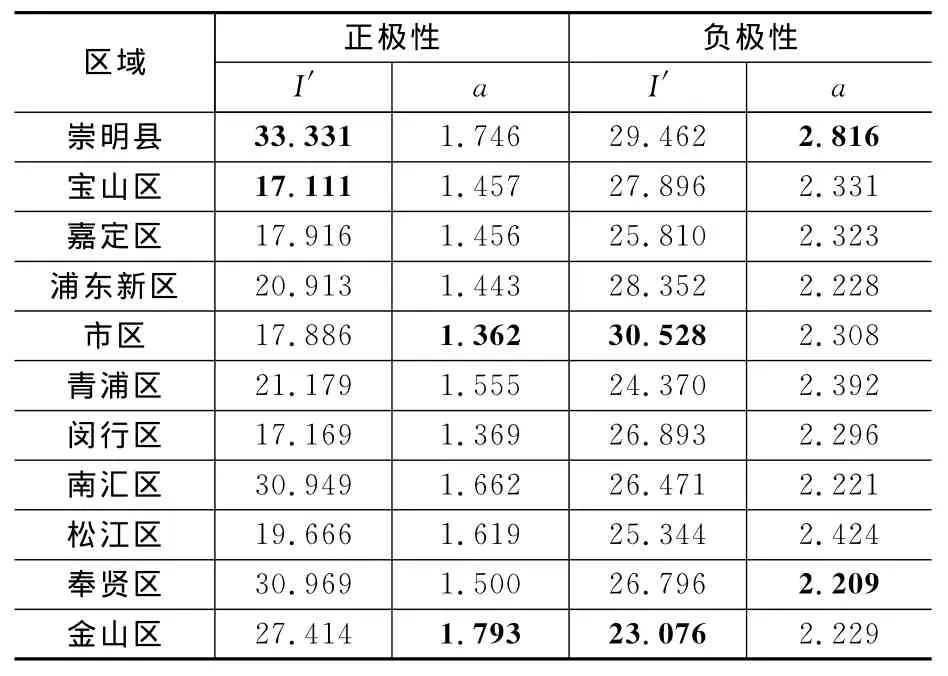
表2 上海各行政区域10年的雷电流幅值分布参数

表2中正极性雷电流幅值分布的中值参数其变化区间为［17.1，33.3］，标准偏差为6.26；陡度系数变化区间为［1.4，1.8］，标准偏差为0.146；而负极性雷电流幅值分布中值参数变化区间为［23.1，30.5］，标准偏差为2.18；陡度系数变化区间为［2.2，2.8］，标准偏差为0.172。体现了上海地区落雷电流幅值分布随地理位置的变化，具有一定的随机性。所得参数整体上与Pobolansky和IEEE Std推荐公式的参数较相近。

由f（I）＝（1－PI）′和表2数据，可得上海各行政区域2001—2010年负极性雷电流幅值的概率密度计算式，如表3所示。正极性雷电流幅值的概率密度计算式这里不再给出，可参考负极性的表达式形式。