推力室多孔面板氢发汗冷却传热分析

高翔宇，孙纪国，田 原

（北京航天动力研究所，北京100076）

0 引言

发汗冷却是膜冷却的极限形式，具有更好、更经济的冷却效果。多孔结构内的发汗冷却原理即冷却剂与热流相反的方向穿过多孔结构骨架中的微孔，通过与多孔结构骨架之间换热将多孔结构的热量带走，并在出流壁面侧形成连续均匀的气膜屏障，阻隔外界热流侵袭。发汗冷却技术广泛应用于超高速飞行器重返大气前端热防护[1]、燃气涡轮叶片以及火箭发动机及喷气发动机喷管热防护等航空航天领域[2-3]。发汗冷却技术在可重复使用航天器领域也有着很好的应用前景[4]。美国RS68，J-2，SSME和日本LE-7等氢氧火箭发动机推力室的喷注器面板都采用金属丝网烧结而成的多孔面板[5]。

目前在对多孔结构壁面内发汗冷却传热过程的理论研究中主要有局部热平衡模型和局部非热平衡模型。局部热平衡模型假设多孔结构中固相和流体有相同的温度，不考虑多孔结构内流体与固体骨架之间换热，进而简化了物理模型方程，可以通过直接求解微分方程获得解析解，但此模型的应用条件也受到限制，适用于多孔结构孔隙率较小、固体导热率较大、颗粒特征尺寸较小的情况[6]。局部非热平衡模型认为多孔结构中固相与流体之间存在温差，考虑了多孔结构内流体与固体骨架之间的换热，更真实的反应了冷却剂在多孔结构内的流动换热状态。本文采用一维稳态局部非热平衡模型，对氢氧火箭发动机推力室喷注器多孔面板的传热情况进行了数值模拟，分析比较了多孔面板材料导热系数、孔隙率、多孔结构颗粒特征直径以及燃气侧热流密度等因素对面板发汗冷却的影响。

1 物理模型和计算方法

1.1 推力室喷注器面板的几何描述

图1为典型氢氧发动机推力室结构示意图，推力室主要由点火器、喷注器和燃烧室等部分组成。喷注器为三底两腔结构，面板位于喷注器的底端，起到固定喷嘴，隔断喷注腔与燃烧室的作用。氢氧火箭发动机推力室喷注器气液喷注、雾化、蒸发和混合过程很快，火焰峰距喷注器面板很近。面板的一侧是3600 K的高温燃气，另一侧是约100 K的低温气氢，面板承受很大的温差应力，极易翘曲变形而造成烧蚀破坏。为此，大多数氢氧喷注器面板采用多孔材料制成，通过渗透少量氢气发汗冷却保护面板，面板的透氢量一般为氢总流量的2%～10%，并且这一小部分发汗冷却剂冷却面板后直接进入燃烧室参与燃烧，不会影响推力室的燃烧效率。

1.2 传热数理模型

多孔面板发汗冷却一维物理模型如图2所示。

发汗冷却剂以同燃气热流相反的方向流经推力室喷注器多孔面板，与其内部固体骨架进行换热，并在另一侧喷出参与燃烧。本文应采用一维稳态局部非热平衡模型式（1）和（2）表达其内部换热过程[7]。面板的冷却剂侧受到低温冷却介质的强冲击冷却，因此可以认为冷却剂侧面板的温度与冷却剂温度相同，发汗冷却剂和面板均为绝热边界，满足边界条件式（3），这一边界条件特征在面板发汗冷却传热试验研究中得到验证[8]。在实际发动机工作情况下，氢氧推进剂在面板燃气侧进行喷注雾化混合燃烧，多孔面板燃气侧的换热状态非常复杂，与推进剂的喷注状态以及燃烧室室压、混合比有关，简化为以给定热流密度值qr的形式作为多孔面板燃气侧热流密度的边界条件式（4）。

固体能量方程：

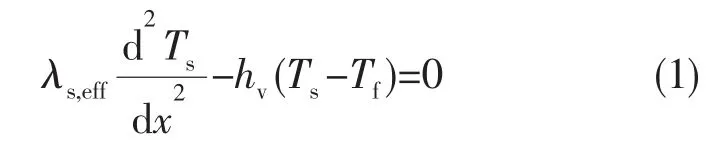
流体能量方程：

发汗面板冷端边界条件：

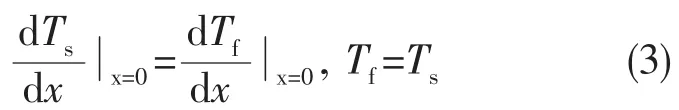
发汗面板燃气侧边界条件：

上述方程式中，λs,eff=1-（）ε λs和 λf,eff=ελf分别为多孔结构和冷却剂的等效导热系数；hv为多孔结构与冷却剂之间的体积对流换热系数，可由式 (5)、 (6)求得[9]。

式中：αsf为多孔结构内部参与换热的单位体积热交换面积；hsf为多孔结构内固体与流体之间的对流换热系数，一般由多孔结构内对流换热经验关系式求得[9～11]；ε为多孔结构孔隙率；dp为基于颗粒堆积床模型给定的多孔结构颗粒特征直径，对于丝网烧结成形的推力室多孔面板，可根据冷态气流试验流阻与渗透率的关系确定其等效颗粒特征直径。

发汗冷却剂在多孔结构内流动应满足流体连续方程式（7）。式（8）为多孔结构中的等效雷诺数定义，式中M=ρu为单位面积上的冷却剂质量流率，当流动速度较低的情况下（Re＜1），其多孔结构内的流动特征符合Darcy定律式（9）；当流速增大 （Re＞1），其流动符合 Darcy-Forchheimer式（10）表示[12]。一般在氢氧喷注器多孔面板内冷却剂流动等效雷诺数Re＞1，因此选择式（10）作为本文的流动动量方程。

流体连续方程：

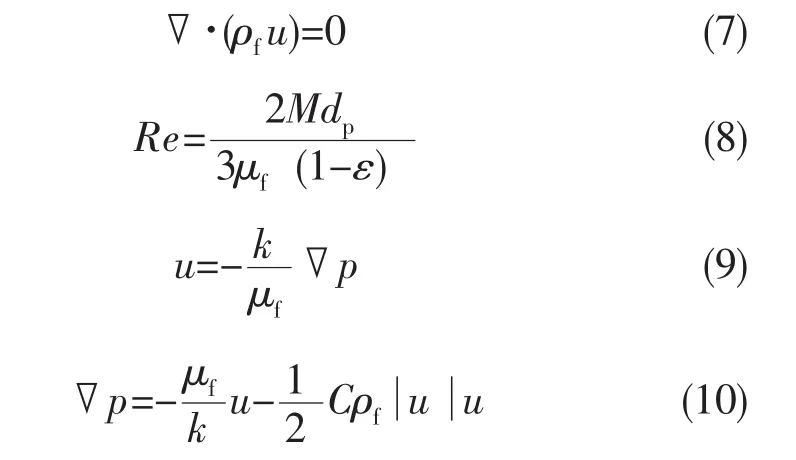
式中：μf为流体动力粘度；ρf为流体密度；k为多孔结构渗透率；C为流动惯性系数。Ergun[13]基于颗粒堆积床模型给出k和C的经验关系式 (11)、 (12)。

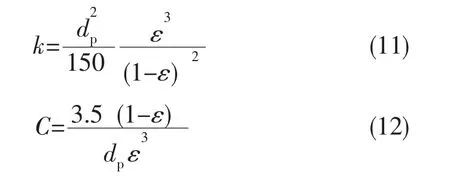
上述计算模型采用Fortran程序语言编程求解，计算求解过程中考虑氢物性随压力、温度的变化，将压力范围5～15 MPa、温度范围100～600 K的氢物性参数[14]以温度、压力二维数组的形式读入程序中，并根据每一计算步的温度、压力差值求解。计算模型不考虑多孔结构固体导热系数随温度的变化。

2 计算结果与讨论

在液体火箭发动机工程应用中，通常推力室喷注器面板两侧的压力及冷却剂入口温度是给定的已知条件。在保持冷却剂入口压力10 MPa、冷却剂出口压力8 MPa、冷却剂氢入口温度300 K不变的情况下，分别改变多孔面板材料导热系数λs、孔隙率ε、多孔结构颗粒特征直径dp和燃气侧热流密度qr，研究上述参数对面板发汗冷却的影响。根据多孔面板发汗冷却试验结果[8]推算得出在燃烧室压力为8 MPa、氢氧混合比为7的情况下，面板燃气侧热流密度约为40 MW/m2。本文围绕导热系数λs=15 W/(m·K)，孔隙率ε=0.1，颗粒特征直径dp=0.15 mm，热流密度qr=40 MW/m2这一基准开展讨论研究。

分别选取材料1不锈钢（15 W/(m·K)），材料2铝镁合金（107 W/(m·K)）、材料3无氧铜（382 W/(m·K)）3种不同热导率的材料作为计算研究对象，保持孔隙率、颗粒特征直径以及燃气侧热流密度不变，研究不同面板材料导热系数对发汗冷却的影响，计算结果如图3所示。计算结果表明面板材料导热率越大，燃气侧面板温度和温度梯度都随之降低，热浸深度随之增大。并且随着面板材料导热率增大，固体与流体换热越充分，两者的温度相接近，满足热平衡模型的假设，因此热平衡模型适用于多孔结构材料导热率较大的情况。

多孔结构的孔隙率ε是影响多孔面板发汗冷却特性的重要参数。如图4所示，在保持其他特征参数不变，并且固定多孔面板两侧压力边界条件的情况下，随着面板孔隙率的增大冷却剂渗透率大幅升高，燃气侧面板温度也明显降低。虽然增大孔隙率可以降低面板温度，但也带来更多的冷却剂损耗，面板的结构强度也将降低，因此设计多孔材料的孔隙率不宜过大，在工程应用中应根据实际情况优化选择多孔面板的孔隙率参数，对于液体火箭发动机推力室多孔面板的孔隙率采用0.1～0.2为宜。

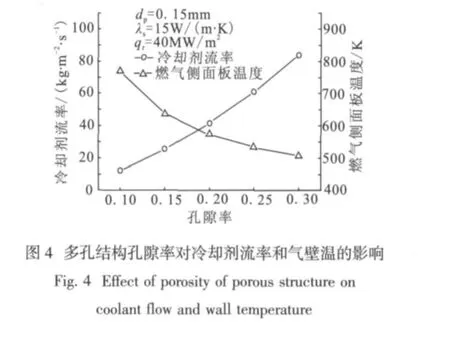
多孔结构颗粒特征直径dp是基于颗粒堆积床多孔结构模型给定的，表征多孔结构物理结构的另一重要参数，宏观上决定多孔结构内微孔的分布情况和单位体积多孔结构内部参与换热的热交换面积的大小，从而影响多孔结构的发汗冷却特性。如图5所示，计算结果表明随着多孔结构颗粒特征直径增大冷却剂流量增加和冷却剂出口温度降低，燃气侧面板温度呈先降低后升高的趋势，多孔结构固体与冷却剂流体之间的温差随之明显增大，表明多孔结构内发汗冷却的体积对流换热系数随着介质颗粒特征直径的增大而大幅降低。当多孔结构固体温度与冷却剂流体温度相差较大时，就违背了局部热平衡模型的初始假设，因此局部热平衡模型不适用于多孔结构颗粒特征直径较大的情况。

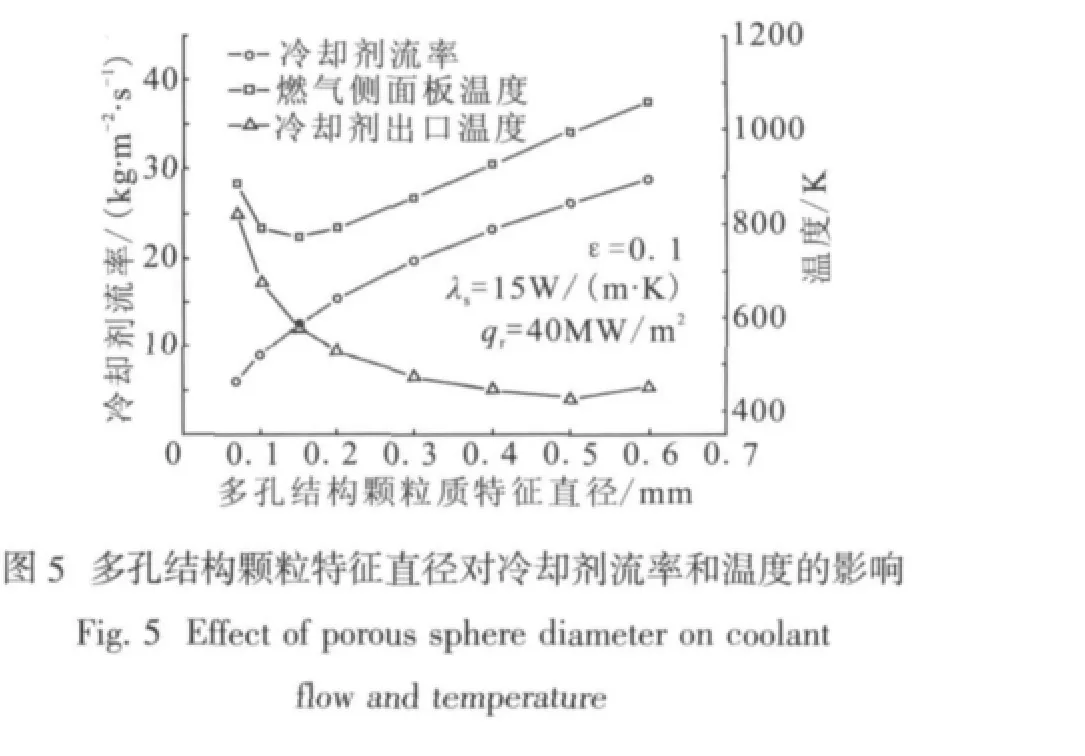
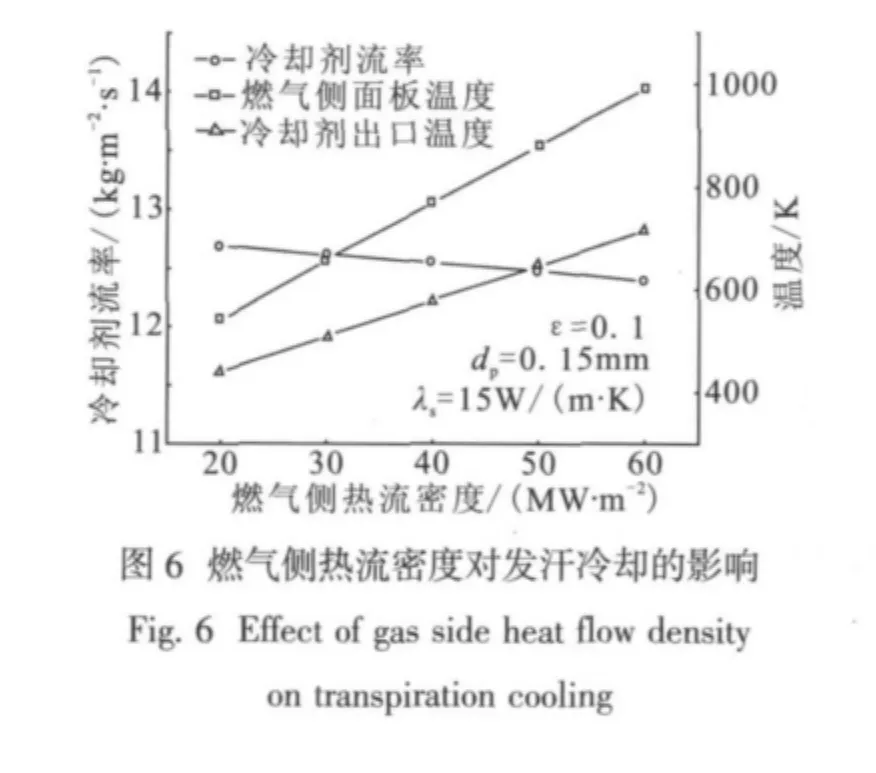
计算面板燃气侧热流密度为20～60 MW/m2情况下的面板发汗冷却情况如图6所示。计算结果表明面板燃气侧热流密度的变化对发汗冷却剂流量的影响较小，随着热流密度的增大冷却剂流量略有降低，燃气侧面板温度和冷却剂出口温度成比例增大。

3 结论

采用一维非热平衡能量方程模型计算研究了氢氧火箭发动机推力室喷注器多孔面板的发汗冷却特性，分析总结了多孔结构固体导热率、孔隙率、颗粒特征直径和燃烧室热流密度等因素对多孔面板发汗冷却的影响。研究结果表明：

1）面板材料导热率越大，燃气侧面板温度和温度梯度都随之降低，选择具有较高导热率的多孔面板制造材料，有利于降低燃气侧面板温度和减小面板温度梯度；

2)孔隙率是控制发汗冷却剂流量和发汗冷却效果的重要参数，一般在0.1～0.2为宜；

3)随着多孔结构颗粒特征直径增大多孔结构固体与冷却剂流体之间的体积对流换热系数大幅降低，但冷却剂流量逐渐增加，因此燃气侧面板温度呈先降低后升高的趋势，采用较小的多孔结构颗粒特征直径有利于增强冷却剂与多孔结构固体骨架之间的换热，多孔结构颗粒特征直径一般不大于0.3 mm为宜。

[1]HUDSON L,STEPHENS C.The X-37 hot structure control surface testing[R].USA:NASA 2006.

[2]BUCCHI A,BRUNO C.Transpiration cooling performance in LOX/Methane liquid-fuel rocket engines[J].Journal of Spacecraft and Rockets,2005,42(3):50-59.

[3]BUCCHI A,CONGIUNTI A,BRUNO Claudio.Investigation of transpiration cooling performance in LOX/Methane liquid rocket engines[J].IAC,2003(10):22-26.

[4]刘双,张博明,解维华.可重复使用航天器金属热防护系统的结构优化进展[J].航天制造技术,2007(3):43-48.

[5]EMRE S,WEI S.Modeling of fluid dynamics and heat transfer through porous media for liquid rocket propulsion,AIAA 2007-5549[R].USA:AIAA,2007.

[6]于淼,姜培学.发汗冷却过程中多孔壁面内的局部非热平衡分析[J].工程热物理学报,2007,28(2):286-288.

[7]JIANG Pei-xue,REN Ze-pei.Numerical investigation of forced convection heat transfer in porous media using a thermal non-equilibrium model[J].International Journal of Heat and Fluid Flow,2001,22(1):102-110.

[8]高翔宇,孙纪国.推力室多孔面板发汗冷却试验研究[J].火箭推进,2011,37(5):9-12.

[9]ACHENBACH E.Heat and flow characteristics of packed beds[J].Experimental Thermal and Fluid Science,1995,10(1):17-27.

[10]DIXON A G,GRESSWELL D L.Theoretical prediction of effective heat transfer parameters in packed beds[J].AICHE J.,1979,25(4):663-676.

[11]VAFAI K,AMIRI A.Non-Darcian effects in confined forced convective flows[J].Numerical Heat Transfer Journal Part A,1997,31:235-254.

[12]孙纪国,王建华.烧结多孔结构的渗透和流阻特性研究[J].航空动力学报,2008,23(1):130-133.

[13]DUKHAN N,PATEL P.Equivalent particle diameter and length scale for pressure drop in porous metals[J].Experimental Thermal and Fluid Science,2008,32(5):1059-1067.

[14]MCCARTY R.Hydrogen technology survey thermo physical properties,NASA SP-3089[R].USA:NASA,1975.