气固二相流中粉体的运动分析

李 奕

（湖北工业大学机械工程学院，湖北 武汉430068）

气力输送就是气固二相流，当气流中含有大量细小固体颗粒，且流动速度足够大时，固体颗粒的流动类似于流体［1－2］.气固二相流中要研究的就是固体颗粒和气流二相之间因为相互作用而形成的流动问题.在颗粒的堆积和粉体力学中，考虑的是颗粒因为相互接触所产生的力和流变问题，并未考虑气流和颗粒之间的相互作用，属于静力学范畴［3］.气固二相流动属于动力学范畴，只考虑气流和颗粒之间因为相对运动而产生的相互作用，不考虑颗粒之间的相互作用［4］.

1 作用在粒子上的气流作用力

气流中粒子的平动和回转运动方程式在直角坐标系（o－x1x2x3）中可以用下式表示［5］

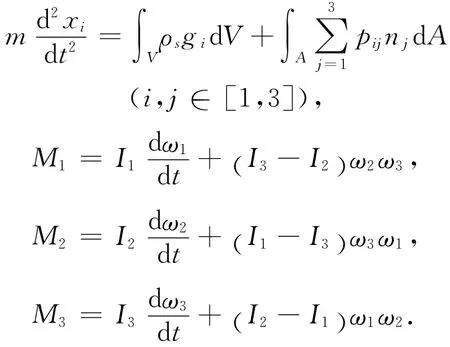
式中：m表示粒子质量，t表示时间，ρs表示粒子密度，gi表示重力加速度，V表示粒子体积，A表示粒子表面积，pij表示粒子表面的气流应力，nj表示法线矢量，Mi表示绕粒子惯性轴回转的转矩，ωi表示粒子的角速度，Ii表示粒子的主惯性矩.

管道内的粒子运动可以用下面方法进行数值解析，将管壁、管道入口、管道出口以及粒子表面作为边界条件带入运动方程式，再求出粒子表面的气流应力pij，将其带入运动方程式，解出粒子新的位置，然后将这个过程反复循环进行.为了正确求解粒子的运动，必须准确计算出气流应力pij，为此，必须保证足够的计算精度.当输送的粒子多数形状都较为复杂时，利用这种方法计算将变得非常困难.于是，通常在计算粒子回转时将粒子的宏观流动简化为简单流动，从而将气流应力pij简化为等效的力.这些力包括气流阻力、横向力、附加质量力、浮力、涡旋力等.在空气输送中，流体密度差别很大的时候，阻力和升力是重要的流体力，需要仔细考虑.

如图1所示，设速度为U的气流中颗粒表面受到的气流法线应力为p，剪应力为τ，则颗粒表面A受到的流动方向的阻力的合力FD和垂直方向的升力FL分别为：

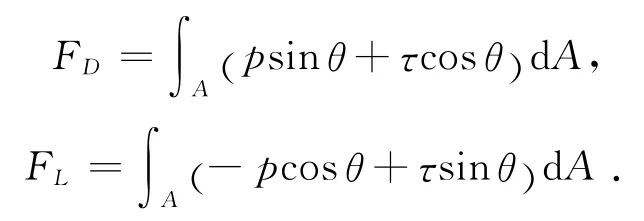
阻力系数CD和升力系数CL可以由

确定.其中，AD、AL分别表示颗粒表面积在各个作用力方向的投影面积.对于粒子流动过程中的输送阻力，各种颗粒有多种测量方法.Morsi等利用雷诺数Re来表达均匀流动中单个颗粒的阻力系数系数C0、C1、C2根据表1决定.粒子群中单个粒子的阻力系数和自由流动的阻力不同，根据Di Felice的研究，可做修正为

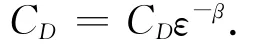
图1 粒子受力模型

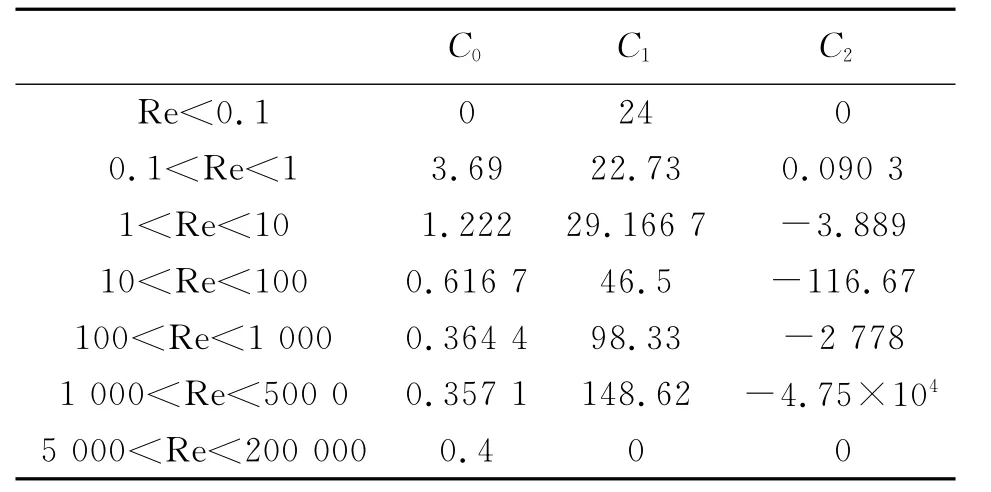
表1 单个粒子的阻力系数

球形粒子的作回转运动时，存在Magnus力.根据日本科学家辻裕的研究，可以利用下式来确定升力系数：

式中，Γ＝ωD／2U，其中ω为粒子的回转角速度.

如图2所示，在气流的速度梯度Π很大的场合，若设粒子和气流的相对速度为Ur，在流动的垂直方向上还受到如图2所示Saff man力的作用.

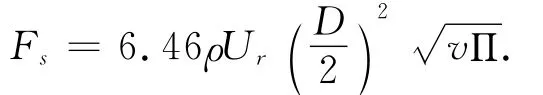
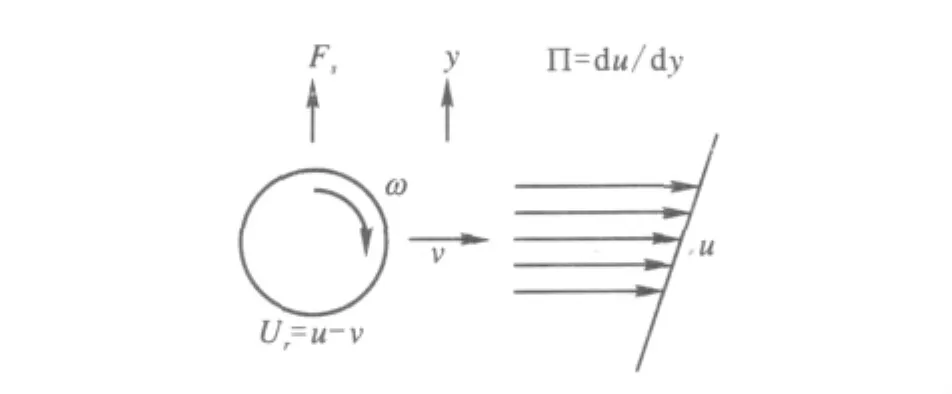
图2 Saff man力模型

2 单个球形粒子的运动和沉降速度

分析在均匀气流作用下，以初速度（vxo，vyo，vzo）从原点投入的单个球形粒子的运动.令x为水平方向，y为铅垂向上方向，z为气流的流动方向（图3）.根据stokes法则，有

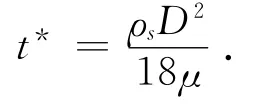
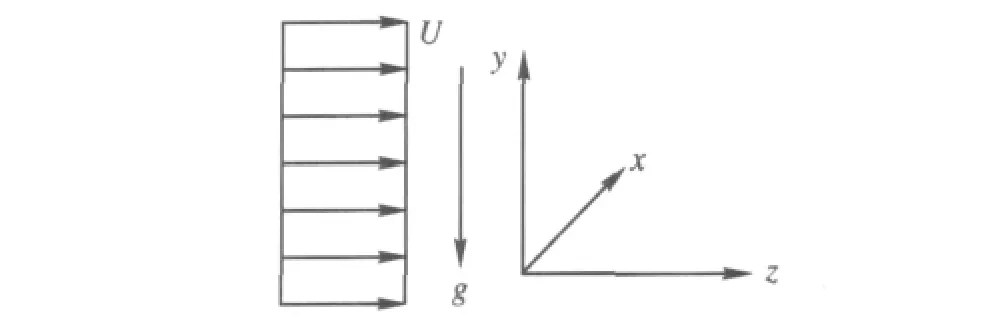
图3 水平气流中粒子的运动

若忽略横向的旋转，可得粒子的运动方程式为：

解得：

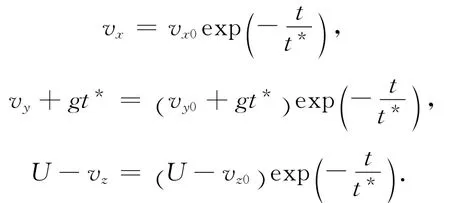
因为t＊非常小，初始状态下vx＝0，vy＝gt＊，vz＝U，因此粒子的运动轨迹为：

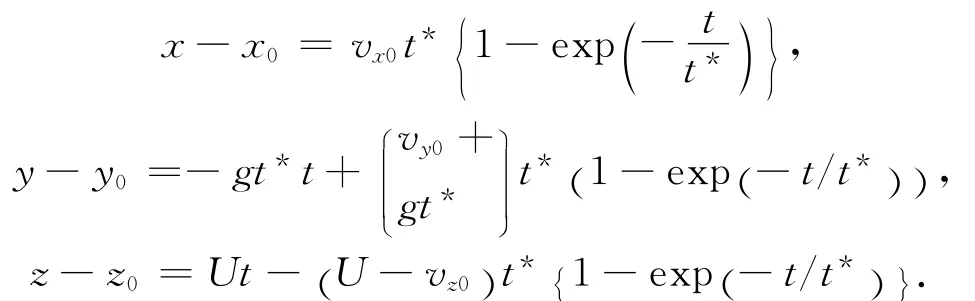
可见，在与气流流动方向垂直的x方向渗入深度取决于vxot＊的大小，而与气流速度U没有关系，将这个渗入深度称为停止举例.t＊是沿粒子的流动方向设定的时间基准，称为缓冲时间，用来衡量粒子惯性的大小.

作为粒子的另一个特性，粒子的最终沉降速度设为ug；粒子在自重、浮力和气流阻力的共同作用下匀速下降时的速度称为最终自由落下速度.对于球形粒子，有

将式（1）带入上式，并利用Re＝ugD／ν，得：

式中，Ga称为伽利略数，也称为阿基米德数.当St okes法则成立时，有

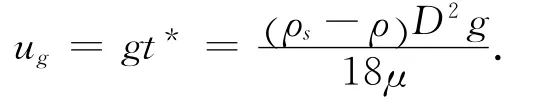
在空气输送过程中，在上升气流中粒子的悬浮速度ug也称为悬浮速度.为了使ug很小的粒子在上升气流中处于悬浮状态，气流作用力也很小.

3 管道空气输送中粒子的运动

在管内流动时，因为管壁的原因，流动受到约束，和管壁发生碰撞会产生能量损失.另外，管内存在大量粒子时，粒子之间也会发生碰撞，能量损失和粒子的运动状态之间存在相互影响［6］.如果把这种粒子群作为流体的一个整体，在定常流状态下可得该式是均一粒子群的方程.式中，c为粒子体积，d s为流动的微小长度，n为粒子个数，D为管道直径，λs为粒子群和管壁摩擦系数，d为粒子直径.

对于满足Stokes法则的粒子群，式（2）可写成

对于流速为u的气流，假设λs为常数时，解出上式得

式中，ζ＝λsut＊／2d，加速结束后的匀速速度称为最终速度，解出该速度为

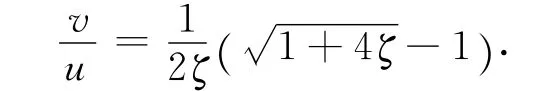
从上式可看出，λs和t很大时，粒子群的速度较小.对于垂直上升的输送状态，速度为

若把CD看作是一个常数，垂直向上输送时，速度为

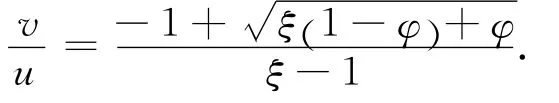
通过以上分析可看出，因为重力的原因，垂直输送比水平输送状态下粒子的速度要更小.

4 静止粉体层的压力损失

当气流从粒子间低速透过时，气流的体积流量Q和流动方向x向的压力梯度d p／d x之间的关系为

这个方程称为达西（darcy）方程.式中，K为透过系数，A为粒子层空隙截面积，利用表观速度U＝Q／A，可得

式中，k＝νK／g称为透过率，压力损失和U成正比，和k成反比.

在空隙率很小的时候，粒子层中的气流可以看成是毛细管聚集形成的毛细管模型.粒子层的流体平均深度

式中，Va为粒子层的空隙体积，St为层内粒子的总表面积的比值，S’＝St／Vs表示粒子层内的粒子群的平均比表面积，Vs表示层内粒子的总体积.如果用ue表示毛细管内的气流流速，Le表示毛细管模型的粒子层等价长度，de表示模型中毛细管的直径，因为de ＝4rh ＝4ε／S’（1－ε），根据 Hagen－Poiseuille法则可得

若气流流过长度为Le的通道所需时间和流过长度为L的粒子层实际所用的时间相等，即Le／ue＝L／（U／ε），则压力损失将上式与式（3）比较，式中，C取1／180～1／150之间的数值.以上公式在Re＝UDSV／ν≤20的情况下成立.

紊流可以认为是在一个粗管道中流动.根据Burke－plu mmer方程，假设摩擦系数为λo，在雷诺数为常数时，压力损失

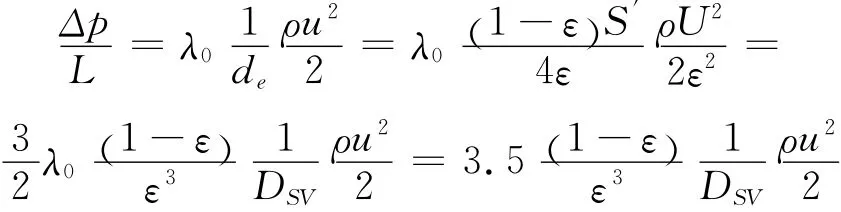
对于范围变化较大的雷诺数Re，根据Ergun公式，有

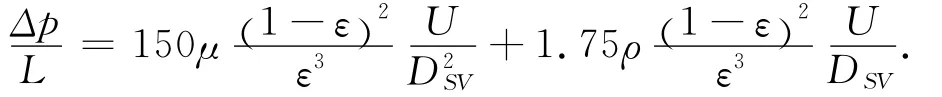
在截面积为A，长度为L的管道中，大小相同的球形粒子在静止的情况下，如果用R表示粒子群中一个粒子收到的气流阻力，N表示粒子个数，压力损失和气流阻力之间存在AΔp＝RN ，因为可得

式中，CDm表示粒子群中一个粒子所受到的阻力系数.

将上式两边分别除以管道长度L，并带入Ergun公式，得

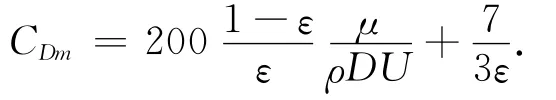
5 结束语

本文分析了在气力输送过程中，粒子受到的气流作用力，推导了单个粒子在气流中运动的运动方程式以及利用管道进行空气输送时，粒子的运动方程式.另外对于气流透过静止粉体层的压力损失表达式进行了推导，为空气管道输送积累了必要的理论基础.

［1］周仕学，张鸣林.粉体工程导论［M］.北京：科学出版社，2010.

［2］谢洪勇.粉体力学与工程［M］.北京：化学工业出版社，2003.

［3］叶 菁.粉体科学与工程基础［M］.北京：科学出版社，2009.

［4］杨 伦，谢一华.气力输送工程［M］.北京：机械工业出版社，2006.

［5］Nedder man R M.Statics and kinematics of granular materials［M］，Cambridge ：Cambridge University Press，1992.

［6］Morsi S M，Alexander A J.An lnvestigation of partical trajectories in two－prase flow Systems［J］.Fluid Mech，1972，55（2）：193－208.