《音程的构成和识别》与手算心算法——《乐理》课教学创新与探索

关玉铭

（甘肃省联合大学 艺术学院，甘肃 兰州 730030）

《音程的构成和识别》与手算心算法
——《乐理》课教学创新与探索

关玉铭

（甘肃省联合大学 艺术学院，甘肃 兰州 730030）

音程的学习决定着乐理这门课程学习的好坏程度，所以结合手算心算的直观教学法，学习音程的结构，然后构成音程，识别音程，为之后的转位音程、等音程、复音程、协和与不协和音程、稳定与不稳定音程、调式中的音程、不协和音程的解决、及音程在音乐中的应用及表现特性等打下坚实的基础.也为今后的和声学与即兴伴奏搭好桥梁.

乐理；音程的构成和识别

如何编配美妙的和弦进行？如何将律动的旋律衬托的恰如其境？需要精湛的演奏技巧，更需要丰富的和声知识.音程知识是和弦的基础，正所谓：“工欲善其事，必先利其器”.要掌握和弦，当以音程知识为先.

音程，是中等师范及中等艺术专业学校，音乐专业所开设的《乐理》这一学科中最重要的教学内容，也是学生继续学习和弦、调式及和声学知识、即兴伴奏等不可缺少的基础.在这一章里，介绍了旋律音程与和声音程、音程的级数与音数、自然音程和变化音程、单音程与复音程、音程的转位、构成和识别音程的方法、等音程、协和与不协和音程、稳定与不稳定音程、调式中的音程、不协和音程的解决、及音程在音乐中的应用及表现特性等十二个方面的内容.从多年教学实践的经验来看，音程的构成与识别这一节的内容如同我们从小学会的个位数的乘法口决一样重要，如果没有这个做基础，多位数的乘法就无法运算，除法就更谈不上学习和应用了，那我们的生活也就无法想象.

所以我认为《音程的构成和识别》一节是音程这一章节中的核心知识，如果这部分内容含糊不清，就无法学习音程中其它部分的内容，所以应做为音程教学内容的重点部分.同时，这一节内容，学生最难掌握.因此，又是教学的难点.现就自己多年的教学经验与学生学习效果让我深深体会到，想要学好乐理知识教学方法起决定性的作用.方法不当，或严格按照教科书的编写顺序和书面语言去讲解此课，学生只有一个感受“难”，枯燥、不易理解、不易学懂，看着书上的谱例、范题，依然不会做题.根本不是其它学科自学就可以学通理解应用的.这样的教学效果往往是学生从音程这一章节开始，和弦、调式之后的内容几乎放弃不学.因为这一环节不通，后边的知识无法衔接.

所以，这就需要寻找一条浅而易见，形象生动的路径去讲解这些知识，怎样才能把复杂的问题简单化，怎样把书面的问题生活化，怎么把记忆的东西理解化、推理化.让学生能轻松、快乐、直观、形象的去理解音程的概念，分类和名称、构成与识别的方法与技巧.然后再将音程扩大或缩小，或进行转位，或进行等音程的变化，这些都会迎刃而解，也就可以激发和调动学生的学习积极性.学生越学越爱学，就可进入良性循环，这种方法就是我多年总结出的手算与心算相结合的办法来学习音程.由于方法直观、简便，学习效果是喜人的.

1 音程概念理解的生活化

音程与路程的比较

路程：这一词的概念，同学们首先会理解为道路由甲地到乙地两地之间的距离为路程.“程”在计算距离，通常计算公里、米、等为计量单位.

音程：与路程有共同之处，“程”也在计算距离，那么“音程”也就是两音之间的距离.

路程有公里、米等做单位，用小时来确定速度.音程不能以公里来计算单位.那么我们用什么呢？首先我们学习音乐，音乐离不开基本音级：

简谱： 1 2 3 4 5 6 7 i音名： C D E F G A B C

其中一个音级是一度，如1-1，#4-#4等都是同一音级就叫一度.二个音级是二度，掰着手指算如1-2，2-3，3-4数了二个手指就是二度.从1-6数了6个手指就是六度.从1-i掰着手指数到8，那么就是八度.

以上得出音程的距离是以度来衡量计算的，但并不精确.我们又从上方大调音阶可以看出里面相邻的两音距离不是平均相等的，而是有半音和全音关系区分的，所以在计算两音距离的时候，就要计算出里面包含的全音和半音的数量，也就是音数，才能精确求出两音的准确距离.

由此我们已知路程的距离需要时间和速度两个条件，那么我们计算音程的距离也就需要度数（也就是音级数）和音数两个条件.我们用它来衡量音与音两音之间听觉上的距离.

若我们想知道甲到乙的路线距离，那么用时间和速度就可以得到答案.要确定两个音之间的距离关系，首先要确定是哪两个音.这就像计算两处相隔的距离一样，要先确定甲和乙分别所在的位置.

当两个音相结合，就构成音程.其中较低的音叫根音，较高的音叫冠音.当两个音相同时，前面或下面的音叫根音，后面或上面的音叫冠音.音程的根音和冠音，结合于我们生活中植物的根茎和国王的王冠.根在下面而冠在上.如此命名即形象又便于理解.

这就不难看出，两音之间的关系有两种不同的状态；一种是有先后的横向关系，也就是分开先后发声，叫做旋律音程（书写记谱时，也要先后书写，不能纵向对齐）；一种是同时的纵向关系，也就是合起来同时发声的两音关系，叫做和声音程（理解为合声音程），所以书写也要上下对齐（除了二度和一度可以靠在一起外）.

2 对比音程进行自然音程的分类命名

以上我们得知了音程的概念和两种形式旋律音程与和声音程后，我们就要学会音程分类、命名，计算音程.要计算就又离不开我们的基本音级：

音名：C D E F G A B C

要学生熟记此音阶，每个相邻的音的距离关系.一个全音等于两个半音，这是学好音程心算的关键步骤.

（1）纯一度：纯净水非常干净，那么我们把同度的任意两个没有音高距离的音，就命为纯一度.如C-C，E-E，#F -#F，它们都在相同的音上没有产生距离，原地踏步，所以也非常协和、干净、好听、为纯一度.

（2）纯八度：听觉上似乎还是原有的音，只是比纯一度听起来厚实、饱满些，也非常协和.如c1-c2,be1-be2，也就是相同的音名，相邻的音组.

大二度与小二度的比较：

C-D D-E E-F F-G B-C等手指数2个指头都为二度，但是比较得出C-D D-E F-G与E-F，B-C不同，为什么不同？

（3）大二度：因为C-D D-E F-G都为全音级关系，称为大二度.

（4）小二度：E-F B-C 掰手指算也是二度，但它们之间是半音级关系，称为小二度.

由此可以推出大三度和小三度：

（5）小三度：如：D-F D-E-F手指数三个指头，为三度.心算半音级出现一次，称为小三度.

（6）大三度：如：C-E C-D-E手指也数三指头，为三度.心算半音级未出现，称为大三度.

大六度和大七度与小六度和小七度推算相同

（7）大六度：如：C-A 经过 C–D-E-F-G-A手指数六下，为六度.心算里面只有E F半音级出现了一次，为大六度.

（8）大七度：如：C-B 经过 C–D-E-F-G-A-B手指数七个，为七度.心算里面也只有EF半音级出现了一次，为大七度.

（9）小六度：如：E-C经过E-F-G-A-B-C手指数6个，心算里面EF、BC半音级关系出现二次，就为小六度.

（10）小七度：如：E-D经过 E-F-G-A-B-C-D手指掰七个，也就是七度，心算里面EF、BC半音级关系出现二次，就为小七度.

纯四、纯五度与增四、减五度的对比.

（11）纯四度：如：C-F经过C-D-E-F四个音，心算里面出了E-F的半音级一次，就叫纯四度.

（12）纯五度：的算法和纯四度相同，如E-B半音级出现一次，就叫纯五度.

我们经常在伴奏谱中会发现C-G-E-G的五度伴奏织体和G C的四度都很协和，所以就叫“纯”度.

（13）增四度：如：F-B经过F-G-A-B手指数到四，为四度.但心算里面没有出现半音级，只有全音级，所以称为增四度.

（14）减五度：如B-F经过B–C-D-E-F手指数到五，为五度.心算B-C半音级出现一次，EF半音级又出现一次，共二次，所以称为减五度.

这样我们在自然音级上，就可得出十四种自然音程（不升高也不降低任何音）.为了便于学生记忆，编成顺口溜，一、四、五、八纯，二、三、六、七大小分，再加增四和减五，十四个种类不可混.

变化音程：除以上十四种自然音程以外的所有音程都为变化音程.

3 音程的运算和判断

3.1 首先：手算度数，心算性质（半音的出现次数）

也就是先前我们只是知道三度、五度、八度等，并没有具体到大小三度，纯五度或减五度，纯八度算，现在我们通过心算半音级的出现次数，很快就可以判断出音程准确的名称和性质.再归类：

3.2 强调和辨别音程的种类

“一、四、五、八”中不要找“大小”，“二、三、六、七”中不要找“纯”.各种音程都可以找“增、减、或倍增、倍减”.

3.3 音程的扩大与缩小

（1）纯音程的扩大与缩小

（2）大音程的扩大与缩小

（3）小音程的扩大与缩小

3.4 正确识别音程和快速构成音程

熟练掌握十四个自然音程里的半音的出现次数和相对应的音程的名称，它就为我们做各种变化音程建起了桥梁.我们就不用死记硬背音程的“音数”，学生可以通过度数及性质，再推算音数，这种方法更便捷.

3.5 冠音与根音升降记号的实际意义：

音程在扩大？还是在缩小？不是看到升号就扩大，看到降号就缩小.根音与冠音位置不同，升降号的意义也不同.

冠音有升号是升高，冠音有降号是缩小.

根音有升号是缩小，根音有降号是扩大.

首先判断出2为根音，7为冠音，手算六度，心算半音出现一次，定为大六度再看冠音b7有一个降号，表示缩小一个半音，大六度就变成小六度.（“六度”为名称，“小”为性质）.

先用手算4-7为四度，再用心算没有出现半音级为增四度.再确定根音#4就缩小一个半音，增四度降为纯四度，在看冠音b7又缩小一个半音，由纯四度降为减四度.

也可用大指在下，食指在上.利用空间建立直观图.

反之如两音扩大：增六度

如：

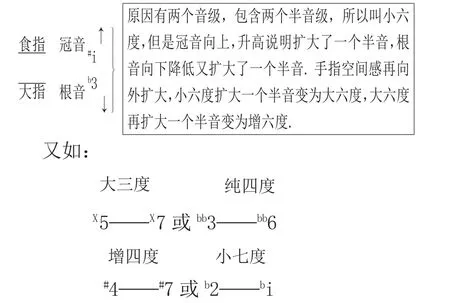
这些音程的计算，同时升高或降底，或同时重升或重降，原有音程的性质不变.

如：音程的构成：给出根音“2”↑向上建立减六度：

手指数6个音到“7”心算半音出现一次，这是大六度，只有大六度缩小降低一个半音才能得出小六度，小六度再缩小降低一个半音才能得出减六度.由此得出“bb7”为所建立的减六度.

再如：给出冠音“i”↓向下做出增四度：

掰手指“i-7-6-5”心算“i-7”半音出现一次是纯四度，纯四度扩大一个半音成为增四度，故根音“5”就要降底一个半音，这样才能扩大成为增四度.

需要特别注意的是：

C-#C或C-bC都为增一度，不能成为减一度，因为它们产生了一个半音，音数没有负值.

以上学生在运算中分清楚扩大和缩小的直观手势、熟练、运用、掌握，再学习复音程、等音程及音程的转位等其它音程知识，都会很简单.

总之，良好的开始是成功的一半.对音程知识的理解和掌握程度，决定着是否能够学好乐理.只有认真地学好音程的构成与识别这种技能技巧，我们才能更好地学习和弦、调式和声等相关知识，才能编配出美妙的和弦伴奏，才能更好的应用在音乐的各个领域.以上是我个人的教学观点，以供参考.

〔1〕李重光.音乐理论基础[M].人民音乐出版社，1962.

〔2〕王晓燕.乐理教材编排与认知心理学关联探微[J].广东技术师范学报，2008（8）.

〔3〕李晓晔.对乐理课程体系设置及教学的一些思考[J].音乐生活，2010.

G642

A

1673-260X（2012）05-0258-03