路径积分法在随机动力系统中的应用

莫协强

（梧州学院 数理系，广西 梧州 543000）

路径积分法在随机动力系统中的应用

莫协强

（梧州学院 数理系，广西 梧州 543000）

路径积分法在随机动力系统中有着重要作用，本文介绍了基于Guass-Lgenedre公式的路径积分法的原理和算法，并研究了谐和激励与随机激励作用下的Duffing一Ryaelihg振子，推导用于计算时间上的平均概率密度路径积分数值表达式，探讨随机跳跃现象存在性和概率密度峰的个数之间的关系.

路径积分法；随机动力系统；Guass-Legenedre公式

它的基本思想是在空间和时间路径积分的离散化,将取代路径和积分、非线性随机动力系统可能有复杂结构的确定性和随机响应反应,Yim和Naess,等等…随机响应分析混沌响应的概率密度,即通过不确定性系统中激励引进随机干扰,混沌吸引子的不确定性系统存在也能有效地使用相空间的随机响应的概率密度演化来描述.本文主要利用路径积分方法研究了非线性随机动力系统混乱的反应.

1 路径积分法的原理

在空间和时间是途径和离散化,而不是整体,这是路径积分方法的基本思想.即通过短期的转移概率密度的连接形式的全球转移概率密度,得到状态向量的联合概率密度函数.虽然每条路径的贡献的定性概念的总和是透明的,但它应该给予的总和更精确的数学定义,路径是一个高阶无限数目的音乐,是道路的间隔什么样的措施应给与不明显.目的是为了给这样的数学定义,该定义是挺麻烦的.路径积分法是最优越的特性可以得到负面,更准确的尾部概率密度.此外,路径积分法也可以计算非平稳信号的系统暂态概率密度和问题,如第一次通过.最简单的定义路径积分方法是连续的过程离散化在空间和时间限制的小格子点通透.然而,一个连续的过程的离散并不是唯一的.因此,对于不同的离散规则,你有许多不同的路径积分方法.为建立路径积分协变的,需要选择特定离散规则,导致许多研究人员并没有被具体的离散规则,提出了各种各样的推导的路径积分法协变.Wehner和wolfer路径积分方法研究首次提出以寻求“非线性随机“FPK方程可得到精确稳态解形式解.给出不确定的道路路径积分的近似解的初始值适当的点,路径积分形式的解决方案可能在平衡热力学领域热力学平衡延续的概念.实际上大部分人致力于用路径积分表示下列FPK方程：

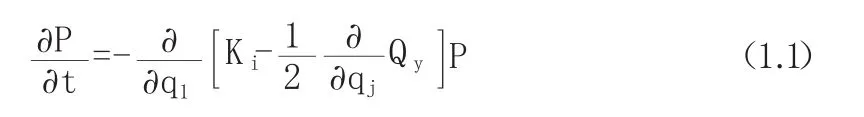
其中P（q1,q2,…,qn,t）是满足上述“非线性随机”FPK方程的概率密度，是扩散张量，是漂移向量，重复下标表示求和.即将方程（1.1）的解表示为如下形式的泛函积分：

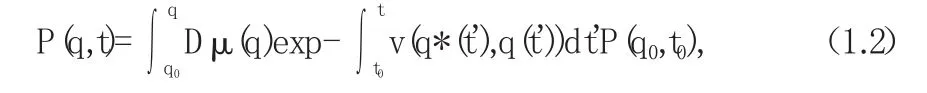
其中Dμ(q)是积分测度，通常看作是Onsgear-Machl up泛函.若使等式(1.2)是协变形式，那就是当来自行星光状态矢量空间的非线性随机点变换,Onsgaer-Machl up功能也根据通常的计算规则了相应的改造,那么问题将变得更为复杂.因此,困难的路径积分是不可能Onsgaer-Machl up唯一肯定的功能.如果你想获得基于路径的非平衡热力学理论一致的积分,那么这个属性是必不可少的.最简单的定义路径积分方法是连续的过程离散在时间和空间充满了小有限网格点.然而,一个连续的离散化过程不仅这样的话,分别对应着不同的离散规则,你有许多不同的路径积分方法.建立了路径积分协变的,需要选择特定离散规则.在所有可能的路径,一个特定的路径由适当的条件决定,最低的原则是表示,此次行动是最桶色条件的一种方式.换句话说.存在一定数量的年代,我们可以计算出,每条路径,经典轨道;是最少的年代的轨道.事实上,真正的条件S只是一个极值.也就是说,如果这路径;X稍作改变,S价值为一阶来表达相同的,所以我们不给出具体如此在各种规则的建议是协变的沿程积分方法.在实际应用中,即使路径积分法的概念具有一定的参考价值,而是解析解和数值,公式(1.2)的计算是不太可能推广到一般的情况,wehner和wol f er首先讨论基于方程(1.2)的数值计算方法,提出了等效离散形式,起点是路径,路径积分或离散网格.的目的是寻求FPK方程可得到精确稳态解(1.1)的解决方案,路径,并能很好的为基础的数值计算方法.路径和通常写成：

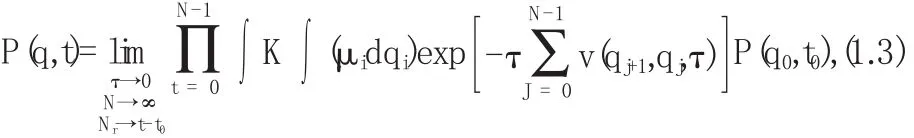
其中 G(qi+1,qi,τ)=μiexp[-τv(qi+1,qi,τ)]称作短时传播子，不同离散规则有不同的G，传播子的唯一条件是它满足方程（1.1）达到O(τ2).确定数值方法的简单的、最准确的路径和公式是：

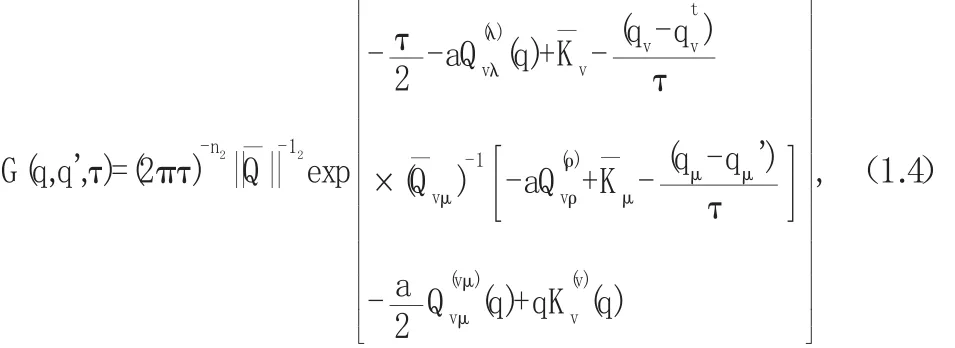
2 基于Gauss-Legendre公式的路径积分法

在许多乔条件出现的特色功能是一种高斯分布,泊松分布假设随机脉冲,从而介绍其二阶近似的指数关系,并得到高斯功能,事实上,一些本质的物理过程看起来像个他们分布.在传统的风险理论,高斯分布符合物理现象.这是因为很多随机出现的综合结果的独立的事情.这就是那个机遇去中心极限定理理论的结论,同样的结论适用于分布的功能.因为许多路径积分可以划分为若干路径积分因素、制度是在一个特定国家和功能,可以写每种模式下的是产品的一个因素.最基本的理念是路径积分在空间和时间离散化、道路、而不是整体,即通过连接短期转移概率密度形成全球转移概率密度,得到状态向量的联合概率密度函数.设(X)t是n维状态向量，其演化概率密度为

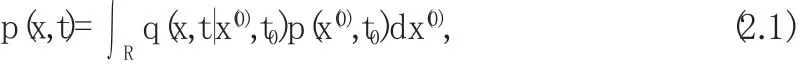
其中q(x,t|x(0),t0)是转移概率密度，由非线性随机动力学系统相应的FPK方程确定，p(x(0),t0)是X（t）在t=t 0处初始概率分布，R 是X（t）的 n维状态空间.将[t 0，t]分成 N 个子区间可得：

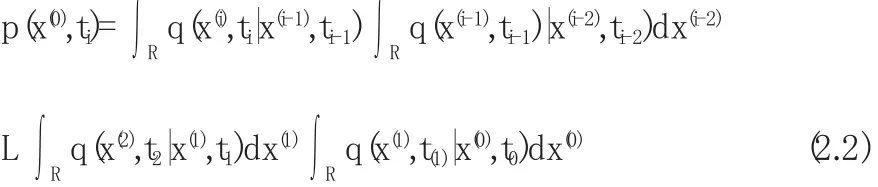
实际上，路径积分是在缩减的状态空间Rx内积分，Rx之外的区域转移概率密度因为充分小而忽略不计.即：

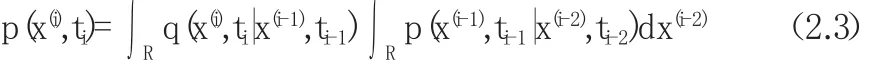
利用不同的插值公式就形成不同的路径积分数值方法.目前主要有两类广泛应用的路径积分数值方法.一种是，Naess等利用三次B样条插值来离散积分式(2.3)，可以计算尾部低于10-6数量级的平稳概率密度.进一步,Naess提出了概率密度的B样条插值的对数函数代替直接在概率密度自身的插值,能明显地提高计算精度和效率.另一个是,玉将(2.3)根据Guass-Lgenedre公式离散化,得到Guass-Legnedre基于路径的积分公式数值计算方法.高斯积分点其他的点概率密度能通过插值.所以,只有我i时刻高斯积分点计算相应的转移概率密度,大大减少了计算量.最终可得到适合编程实现的表达式.一维情形即：

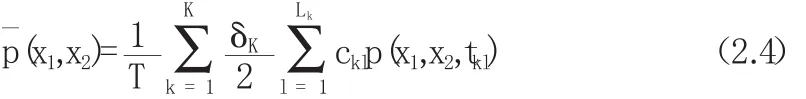
其中K是子区间数,Lk是第k子区间的高斯积分点数，δk是第k子区间的长度，xkl是高斯积分点，ckl是相应的权值.这种方法的优点是没有重新构造插值函数数值积分团聚的,可以直接利用Guass-Lgenedre离散积分公式的类型(2.4).对时变系统,特别是膨胀系数漂移或包含一个传播周期函数的系统,它的时刻就在时间迫使一个骑表达期刊,用简单的方法是通过求解一个周期的时间步ChangShang力矩方程出发.每一刻的解方程周期保持不变,为下星期期间短期转移概率密度的均值和方差的估计.路径积分的数值方法,主要计算是一种转移概率密度的近似,因为相同的电力系统的时候,正好方程表达不依赖时间的,只要计算一下方程;不为高斯白噪声的动态激励机制,一般没有办法直接转矩方程d只有通过开拓系统d系统推力矩方程出发,再用路径积分扩张维数值对应的FPK方程可得到精确稳态解高维系统的分析.噪音强度在一定的非线性随机系统状态估计的概率密度演化可以用来描绘了混沌算子的吸引结构特点.

3 路径积分法基于Gauss-Legenedre公式求解时间上平均概率密度

对时变系统,特别是漂移或包含在扩散系数的周期函数的系统,介绍了概率密度定义的平均时间.

其中T=2π/ω,ω一般是谐和激励或周期系数的角频率.当（3.1）式中t'充分大，在整个谐和激励周期T上平均的概率密度可逼近系统响应的近似平稳概率密度.将Yu的路径积分数值方法推广到时间上平均的概率密度的计算，不难导出利用Gauss-Legnedre公式计算平均概率密度的表达式.即积分表达式(3.1)可离散成如下的Guass-Legendre积分表达式

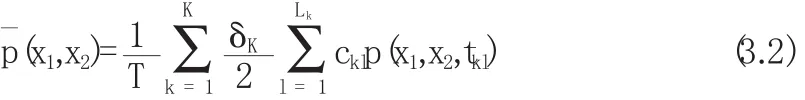
其中K是[t'，t'+T]内的子区间数，Lk是第k子区间的高斯积分点，δK是第k子区间的长度，每一tkl是一个周期内的高斯积分时刻，而ckl是相应的权重，而p(x1,x2,tkl)的计算可直接参考上面的计算方法.Guass-Legnedre于使用路径积分公式法研究了高斯白噪声的冲击只有几个随机非线性动态系统,结果表明该方法在计算尽头的一个更小的概率密度是历史上其他数值方法精度高,本研究是首次通过更重要.合理假设短期转移概率密度为高斯分布,利用高斯三种方法已关闭的力矩方程出发,推导出能算出这道短的转移概率密度的一阶矩和二阶矩.在此基础上,利用路径积分法求解系统的平滑概率密度.不同于简单形状的激情,基于路径积分方法Guass-Lgenedre公式的随机性和冲突,促进共同作用的非线性随机动力学系统,利用非线性动态系统参与的随机研究更为复杂.这些研究结果将和其他数值方法的结果进行了比较,得出了计算尾概率密度具有较高的计算精度.

4 结语

在路径积分对几串理论的这些应用中，如果被积函数是高斯型的.那么我们就可以大量地应用这个技术.这些问题正好都是一些用其他方法也可以解决的问题，不一定要用路径积分.人们可以有理由怀疑路径积分有无实际用途.如果问题不是高所型的，则至少可以用路径积分研究它并将其公式化.然而，路径积分方法使一个问题的各种表述方式之间可以迅速地相互转换，并且常常清楚而迅速地得到关于某个关系式的提示，而用更通常的方式推导它会要慢一些.

〔1〕李杰.随机结构分析的扩阶系统方法(Ⅱ)——结构动力分析[J].地震工程与工程振动,1995(04).

〔2〕李杰.随机结构动力分析的扩阶系统方法[J].工程力学,1996(01).

〔3〕廖松涛,李杰.随机结构正交展开分析的Ritz动力聚缩法[J].计算力学学报,2002(01).

〔4〕李杰.复合随机振动分析的扩阶系统方法[J].力学学报,1996(01).

〔5〕马少娟,徐伟,李伟,靳艳飞.基于 Chebyshev多项式逼近的随机vanderPol系统的倍周期分岔分析[J].物理学报,2005(08).

〔6〕孙晓娟,徐伟,马少娟.含有界随机参数的双势阱DuffingvanderPol系统的倍周期分岔[J].物理学报,2006(02).

〔7〕马少娟,徐伟,李伟.基于Laguerre多项式逼近法的随机双势阱Duffing系统的分岔和混沌研究 [J].物理学报,2006(08).

〔8〕徐伟,方同,戎海武.有界窄带激励下具有黏弹项的 Duffing 振子[J].力学学报,2002（05）.

〔9〕戎海武,徐伟,孟光,方同.谐和与随机噪声联合作用下非线性非线性随机系统的响应[J].应用力学学报,2001（04）.

〔10〕戎海武,徐伟,王向东,孟光,方同.窄带噪声作用下二自由度非线性非线性随机系统的响应[J].力学学报,2001（06）.

〔11〕朱位秋,黄志龙,应祖光.非线性随机动力学与控制的哈密顿理论框架[J].力学与实践,2002（03）.

〔12〕沈仙华,李璋静,赵玉林.非线性随机的单自由度系统相加型联合共振[J].科学技术与工程,2009（18）.

O172.2

A

1673-260X（2012）05-0009-03