基于元胞自动机制度下组织化群体行为的模拟研究
2012-10-10孙绍荣
夏 亭, 孙绍荣
(上海理工大学 管理学院,上海 200093)
现今的许多社会事件均具有群体性的特点,即同一类行为的聚集涌现,如某单位或者地区的集体腐败等.此类群体性事件的行为主体均可认为是组织化群体.组织化群体的概念广于正式组织群体,其可以没有确定的组织形式和结构,因共同的利益、需要及生活背景等而形成松散式集体,且往往有不同的层次,具有一定的联络方式和凝聚力[1].在这些群体性事件中,组织化群体有意或无意地采取集合行动,形成规模,对社会造成一定的影响.尤其是当坏的行为聚集涌现,将比分散的坏行为更难以应对和矫正.因此,对这类行为的研究具有重要的现实意义.
对于组织化群体,国内研究较多的是农业生产的组织化群体、社会特殊身份(如农民工)的群体以及黑恶势力的组织化群体.孙正[1]针对组织化群体内成员开展如行为动因、行为心理等方面的分析,并提出控制策略.冯云霞[2]针对良性的组织化行为作了深层的定性分析及验证.胡斌等[3]将企业的非正式组织看成概念化的组织化群体,对员工的忠诚度进行模拟.王玲等[4]分析了网络群体性事件的特点.国外研究的重点有以下几个方面:a.从群体内部的角度研究组织化群体如何通过通讯和信息交换达到群体的更新[5],从团体培训者的角度研究预测组织化行为的方法[6];b.针对具体行为群体(如交通流、黑恶势力等)提出管理对策[7];c.研究组织化群体对社会其它方面的影响,如个体行为与社会反射性影响之间的关系[8].然而,以往的研究都是基于定性的分析,没有对群体行为演化的全局进行分析与把握.对于有坏行为倾向的组织化群体,应该给予更多的关注,但现有文献的研究仅限于定性的或局部的研究.
国内外用元胞自动机(CA)方法研究动力学系统由来已久,但多用于对自然系统的研究,在社会科学领域则多用于证券投资、金融等领域[9-11].如用于各种交通线路下的交通流及其它交通行为模拟[12-13]、流体动态与断层的地质化学形态模拟[14]、计算机网络的复杂性行为模拟[15].对元胞自动机的另一研究方向是CA纯理论的拓展,如研究邻域的定义规则对全局的影响[16]、CA的拓扑结构和元胞的邻域参数与演化结果的关系[17]、CA稳定状态下周期现象和混沌现象[18].近几年也有用于社会行为方面的研究,如从众行为、员工行为模拟[19-20],研究可重构计算的动态行为模拟[21],改变元胞状态属性以模拟社会个体改变行为的不同步性[22].但仅仅是对脱离社会性质的个体行为或特定事件下的大众行为进行分析,或是实证性的研究,并未基于社会群体的特点而对行为进行有目的的研究,也并未从CA模拟的角度对组织化群体这一制度下的管理对象进行研究.
CA模型从复杂系统的视角出发,利用人工智能和计算机科学领域的成果,在微观层次上构造个体(元胞),微观个体的总和形成宏观结果,是一种自底向上(bottom-up)的研究方法[9-10].本文根据制度设计理论,采用MATLAB编程技术和图像工具包处理数据和图形图像,融合CA模型方法与数学模型方法,即从微观上确定行为转变规则,从中观上观测并对某些聚集行为加以外力(通过引入行为惩罚机制的方法),从宏观上研究演变趋势及规律(通过函数拟合的方法),旨在模拟组织化群体中的行为演变和管理制度对群体行为的规范作用.
1 基于CA模型的组织化群体的行为演化模型
1.1 CA原理与变量定义
元胞自动机(CA)通常由元胞空间、元胞、邻居和局部规则这4部分构成,表示为集合(Ld,S,N,f).L为空间的规模,d为空间的维数;S(s,p)表示一个元胞,s为元胞的状态向量,p为元胞的影响力属性;N(N1,N2,…,Nn)为邻居向量,n为邻居个数;f为局部规则,元胞在t+1时刻的状态根据局部规则以及其自身和邻居在t时刻的状态来决定,可以表示为St+1=f(St,Nt)[9-10].
1.2 建立行为演化模拟的初步模型
现对本文CA模型的四要素分别进行定义,构建行为演化模拟的初步模型,记为模型1.
a.元胞空间.在二维空间中,定义100×100个元胞.使用MATLAB计算工具定义101×101个网格,边界处采用随机数处理.
b.元胞.一个元胞代表现实中某组织化群体中的一个成员.定义元胞状态集为{好的行为a,中立观望行为b,坏的行为c},对这3种状态分别赋状态值s={1,0,-1},su,v代表位于u行v列的元胞的状态值.A={状态为a的元胞},B={状态为b的元胞},C={状态为c的元胞}.pu,v(0<pu,v<1)为位于u行v列的元胞对邻域内元胞的影响力,用来刻画群体内成员之间的联系程度,该影响力pu,v由元胞某时刻所处的状态集确定,定义

式中,M为定义的“领导元胞”,即所研究的群体中的中心人物和骨干分子.
状态为b的元胞对其它元胞的行为选择无影响力.
c.邻居.考虑到人在群体中的实际交往情况,采用Moore 8邻域型.
d.状态转变规则.对于i行j列位置的元胞,用迭代次数T表示模型演化系统的时间刻度t,遵循以下状态转变规则:
(a)在t时刻为b状态,即st=0,若,则在t+1时刻,b转变为a;若,则在t+1时刻,b转变为c.考虑到行为演化模拟的目的及运算时间,b在下一刻不能维持b的状态.
(b)在t时刻为a状态,即st=1,且对于su,v∈C,有

则在t+1时刻,a转变为b;否则,元胞状态不改变.
(c)在t时刻为状态c,即st=-1,且对于su,v∈A,有

则在t+1时刻c转变为b.为体现在现实中坏的行为往往很难通过自身或群体内周围邻居的力量来纠正,c元胞附近邻居大约有6个状态为a的元胞,该元胞的状态才发生改变;否则,元胞状态在下一刻不改变.
(d)在自然条件下,每个单位时间内,每个a状态均以0.1%的概率转变为b,每个b状态以0.1%的概率转变为c.
以随机数法对每个元胞赋予初始状态,其中,A所占比例为20%,C比例为10%,B比例为70%.定义此初始比例为比例1.图1为T=0时的演化界面.
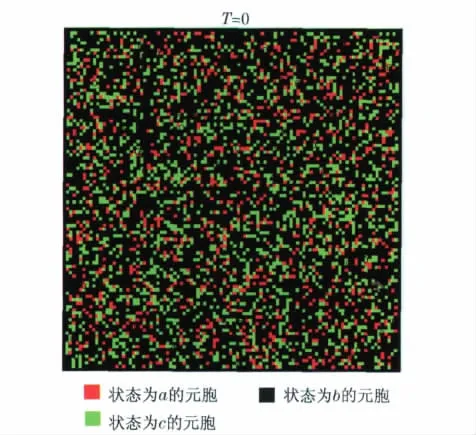
图1 元胞的初始状态Fig.1 Original states of cells
1.3 改进的模型
图2为元胞空间根据前面确定的模型1,经过700次迭代得到的演化图,此时系统已趋稳定,99%的元胞的状态不再改变.为模拟组织化群体的层次性,以小圆圈在图中标记出“领导元胞”,即影响力比普通元胞大的元胞.
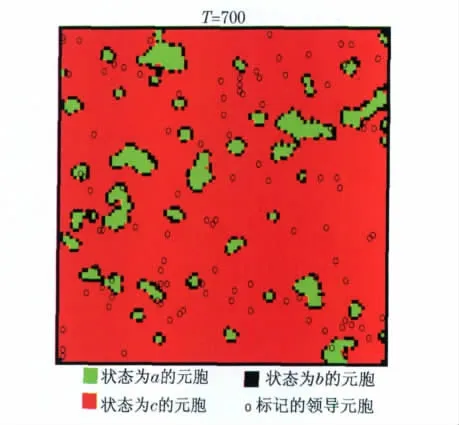
图2 模型1迭代到第700次时的演化结果Fig.2 Result of model 1iterating 700times
观察模型1的演化过程可知,随着时间的推移,状态c将越来越多,状态a和状态b一步步减少,直至各个状态c的团体相连,状态b消失,而状态a将维持在较小且稳定的面积上.通常群体内部很难纠正自身的错误行为,若任其发展,则会愈演愈凶,这正是社会上的一些群体性坏事件的特点,只能靠外部强制力量来改变群体的发展趋势.由此改进,得出模型2,即加入外力惩罚机制,以模拟社会制度对群体行为的规范作用.
现对模型1进行改进,记为模型2.在模型1的状态转变规则中,加入一条惩罚规则,即当t时刻相连(互为邻居则定义为相连)的c元胞的个数达到n时,则在t+1时刻,该相连的n个元胞的状态c转变为a.
图3为模型2在系统达到稳定时的截图.
需要对此模型说明以下两点:a.因状态转变规则里设置了单位时间内元胞以0.1%的概率自变异,故稳定的具体定义为某次迭代前后所有的状态发生改变的元胞不超过15个,即允许浮动0.15%.b.可以预见,有限次数的惩罚并不能使系统永远保持在稳定状态下.随着元胞的自然变异,元胞之间的制约逐渐打破平衡,c元胞的数目必会增大到阈值,从而开始新一轮的惩罚.
图4为比较加惩罚机制前后,c元胞的个数对比.以n=1 000为例.迭代到200多次之后,c元胞的总数Sc几次直线下降,最终以一较低的值保持稳定.

图3 模型2迭代到第477次时的演化结果Fig.3 Result of model 2iterating 477times

图4 对比模型1与n=1 000时的模型2中c元胞总数Fig.4 Compare model 1with model 2for total ccells when n=1 000
2 基于模型2的参数分析
现分别改变模型2中的各个参数,以考察对系统演化的影响,着重观察c状态元胞的聚集及总数的变化.在系统演化的中期、后期及稳定后,中立元胞的总数很小,且位置几乎固定,因此,a状态元胞的变化与c状态元胞的变化相反.
2.1 改变元胞的影响力参数
a.改变u行v列位置的元胞对邻居元胞的影响力.
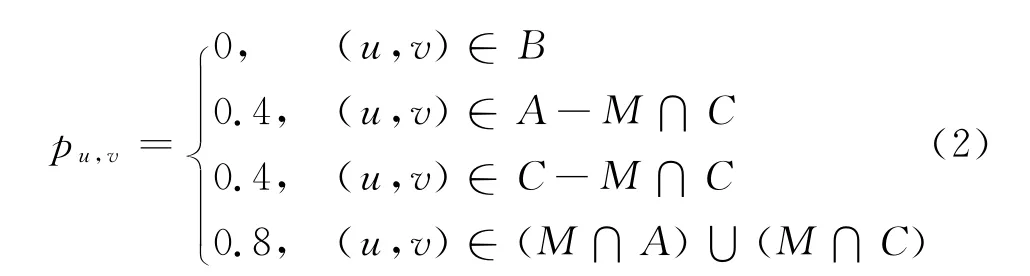
即加大元胞间的影响力,其它的规则均不变,运行模型2以观察结果.
b.改变u行v列位置的元胞对邻居元胞的影响力.

即减小元胞间的影响力,其它的规则均不变,运行模型2以观察结果.
由式(1)和式(2)得到的C集合元胞总数,可画对比图,如图5和图6所示.其中,惩罚阈值n分别为1 000和1 500.得到A集合元胞总数,可画对比图,如图7所示(见下页).

图5 惩罚阈值为1 000时3种影响力参数下模型2的c元胞总数Fig.5 Compare total c cells in three kinds of parameters when n=1 000

图6 惩罚阈值为1 500时3种影响力参数下模型2的c元胞总数Fig.6 Compare total c cells in three kinds of parameters when n=1 500

图7 惩罚阈值为1 500时3种影响力参数下a元胞总数Fig.7 Compare total acells in three kinds of parameters when n=1 500
结合图5~7的两两比较可知,当n相同时,在式(3)条件下模型2的惩罚效果明显比式(1)和式(2)的好,稳定时c元胞维持在较低的水平,a元胞维持在较高的水平.当n增大时,在式(3)定义的影响力条件下模型2的惩罚效果更明显.因此,在一个组织化群体中,若未知所受影响是好是坏(邻居的状态是随机获得),减小元胞影响力,将使群体中的坏行为减少、好行为增加;增大元胞影响力,将使稳定时群体内坏的行为增多,且影响力大于40%时,群体内坏的行为显著增多,惩罚机制几乎失去效用.
2.2 改变初始比例
改变元胞的初始比例,定义为比例2.A的初始总数占元胞空间的比例为20%,C所占比例为5%,B所占比例为75%.以n=1 500为例运行模型2,如图8所示.
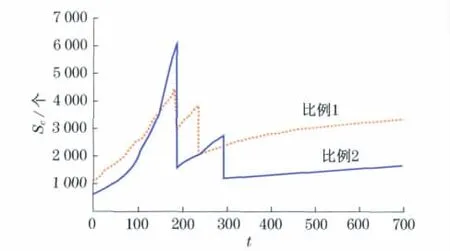
图8 n=1 500时两种初始比例得到c元胞总数的对比Fig.8 Compare total c cells in two kind of initial proportions
比例2下的c元胞总数明显低于比例1下的,能使稳定时群体内坏行为总数显著降低,但初期坏元胞的演化规律改变不大.本例中C的初始比例由10%降为5%,使稳定后坏行为比例下降了至少一半.
2.3 改变惩罚条件
定义观测力度P(C)为制度观测群体内坏行为的能力[23],模型中表现的是对状态为c的元胞进行惩罚的临界条件n,可令

则P(C)=1,意味着当群体内有1/10的相连的坏行为时,制度便能察觉,并给予惩罚.
定义制度效力J衡量该制度维持群体的好行为元胞和中立行为元胞的总体所在的比例水平[23].0<J<1,即

式中,Mc为模型2中C的总数在系统中所占比例的最大值,代表群体中坏行为的水平.
在模型2中,仅改变n的取值,在Matlab中多次运行模型,待得到稳定的结果,记录C的水平,得到图9中的散点.用Fit工具拟合n与Mc的函数关系,得到图9中的曲线.由运行结果得到的n与Mc,经式(3)和式(4)换算得出P与J的值,画出折线图,如图10所示.

图9 拟合Mc与n的函数关系Fig.9 Fit out the relationship of Mcand n

拟合度为0.806.
由模型2得出的数据绘图,得到观测力度与制度效力之间的关系,因为由n到P(C)的变化是非线性,导致数据集中在0.2~0.6的区域,而在其它区域零星分布,不利于函数拟合,因此,本文首先对Mc与n进行拟合,再根据式(3)~(5)得出J与P的函数关系.


图10 观测力度P与制度效力J的原始数据图Fig.10 Original data about observation degree Pand observation effectiveness J
拟合后J与P的关系示意图如图11所示.

图11 模型2观测力度与制度效力的关系图Fig.11 Diagrams about observation degree and observation effectiveness in model 2
在模型2设定的条件下,得到图11中P与J的函数关系,由此可以对J(P)函数进行数学分析.如制度效力与观测力度呈正相关,对于所要求达到的制度效力(如坏的行为在群体中所占比例),可以得知相应的所需观测力度的阈值.
3 结束语
由上述分析的结果得出以下结论:
a.邻居影响力参数对模拟结果的影响.在不能确定所受影响的好坏,即来自邻居的影响近似随机数时,加大群体内成员间的影响力,将使群体内的坏的行为更多;减小该影响力,将遏止坏行为的增多和聚集,并使群体稳定时的坏行为处在更低的水平上.当成员之间的影响力达到40%时,坏行为显著增多,且惩罚制度几乎不能遏制该种涌现和聚集;当成员之间的影响力低于25%时,坏行为的比例几乎能维持在初始比例上.因此,在管理具有坏行为倾向的群体时,若能控制其成员间的影响力在25%以下,则能减少社会上一些群体性事件的发生.对于群体内的成员,若能确定来自邻居的影响是好是坏,则可尽量减少来自坏行为邻居的影响,同时加大与好行为邻居的联系力度;若所受的影响近似随机数,则应尽量减少来自邻居的影响.
b.各种行为的初始比例参数对均衡的影响.减小群体内的坏行为的初始比例,对于系统演化初期坏行为的聚集速度并无改变,但系统稳定后坏行为所占比例将显著降低.当坏行为初始比例在10%以下时,系统稳定后的结果表现出很大的初始敏感性,即坏行为的初始比例对稳定时坏行为的水平有较明显的正比关系.因此,群体的管理者应尽量在群体形成的初期控制住坏行为的比例,若能将坏行为的初始比例控制在10%以下,则改变初始坏行为水平将对稳定后群体的坏行为水平有极大的影响.
c.惩罚规则的阈值n对均衡的影响.改变惩罚规则的阈值n,即改变制度对该组织化群体中的坏行为的观测力度.增大力度,群体坏行为变少,制度效力变高;减小力度,群体坏行为增多,制度效力变低.
对于在群体外的管理者,可设计“监测-惩罚”的机制来管理群体,对监测到的坏行为予以矫正,好行为可以予以表扬使之保持.控制惩罚阈值n尽量小,即监测力度越大越好,得到的制度效力与观测力度关系如图11所示.若加入“管理者具体的监测成本”这一参数,可结合本文得到的制度效力与观测力度的关系式,得到最优的监测力度,即使“制度效力/监测成本”最大的惩罚阈值n.
改进规则使模型更贴近现实社会中的组织化群体,将此研究思路推广到组织化群体以外的行为研究上,对制度效力与观测力度之间的拟合和函数分析更透彻,将是作者今后进一步的工作.
[1]孙正.组织化群体:关于群体性事件参与者的基本分析[J].中国人民公安大学学报,2004,20(5):28-31.
[2]冯云霞.沟通、意义和组织化行动研究[J].学海,2007(1):172-176.
[3]胡斌,殷芳芳.集成CA与QSIM的非正式组织群体行为演化的定性模拟[J].中国管理科学,2005,13(4):130-136.
[4]王玲,王东.防范基于网络组织群体性事件研究[J].广州市公安管理干部学院学报,2006,62(3):29-31.
[5]Choo R K K.Organized crime groups in cyberspace:a typology[J].Trends in Organized Crime,2008,11(3):270-295.
[6]Han J.Real-time multiple people tracking for automatic group-behavior evaluation in delivery simulation training[J].Multimed Tools Appl,2011,51(3):913-933.
[7]Duyne P C,Beken T V.The incantations of the EU organised crime policy making[J].Crime Law and Social Change,2009,51(2):261-281.
[8]Morgan J H,Morgan G P.A preliminary model of participation for small groups[J].Compute Math Organ Theory,2010,16(3):246-270.
[9]应尚军,范英,魏一鸣.单支股票市场的元胞自动机模型及其 动 力 学研 究 [J].系 统 工 程,2006,24(7):31-36.
[10]张廷,高宝俊,宣慧玉.基于元胞自动机的创新扩散模型综述[J].系统工程,2006,24(12):7-15.
[11]杨善林,朱克毓,付超,等.基于元胞自动机的群体决策从众行为仿真[J].系统工程理论与实践,2009,29(9):116-125.
[12]Nelson P.On driver anticipation,two-regime flow,fundamental diagrams,and kinematic-wave theory[J].Transportation Science,2006,40(1):165-178.
[13]Nagel K,Wagner P,Woesler R.Still flowing:approaches to traffic flow and traffic jam modeling[J].Operations Research,2003,51(4):681-710.
[14]Boschetti F.Controlling and investigating cellular automaton behavior via interactive inversion and visualization of the search space[J].New Generation Computing,2005,23(2):157-169.
[15]Shuai D X.A novel network behavior model based on generalized cellular automaton[C]∥ICIC.Heidelberg:Springer-Verlag Berlin,2008:790-798.
[16]Nishio H.How does the neighborhood affect the global behavior of cellular automata? [C]∥ ACRI.Heidelberg:Springer-Verlag Berlin,2006:122-130.
[17]Bäck T,Breukelaar R.Using genetic algorithms to evolve behavior in cellular automata[C]∥ UC.Heidelberg:Springer-Verlag Berlin,2005:1-10.
[18]Jiménez-Morales F.An evolutionary approach to the study of non-trivial collective behavior in cellular automata[C]∥ ACRI.Heidelberg:Springer-Verlag Berlin,2002:32-43.
[19]孙绍荣,焦玥.突发社会安全事件下大众羊群行为的演化模拟及行为族现象[J].上海理工大学学报,2008,30(1):147-156.
[20]胡斌,张德斌.基于元胞自动机间距识别的员工行为模拟方法[J].系统工程理论与实践,2006,26(1):83-96.
[21]Weinert W R,Benitez C,Lopes H S,et al.Simulation of the dynamic behavior of one-dimensional cellular automata using reconfigurable computing[C]∥ARC.Heidelberg:Springer-Verlag Berlin,2007:385-390.
[22]Fatès N,Regnault D,Schabanel N,et al.Asynchronous behavior of double-quiescent elementary cellular automata[C]∥Proceedings of the 7th Latin American Conference on Theoretical Informatics.Heidelberg:Springer-Verlag Berlin,2006:455-466.
[23]孙绍荣.行为控制制度的数学描述与有效性分析[J].系统工程学报,2008,23(1):228-232.
