基于多核心工作站机群的并行介数算法
2012-10-10毛国勇
毛国勇, 张 宁
(1.常州工学院 电子信息与电气工程学院,常州 213002;2.上海理工大学 管理学院,上海 200093)
大规模网络分析在许多重要领域,如社会网络、信息传播网络和生物网络等领域中有着广泛的应用[1],而介数[2](BC)是分析大规模复杂网络时广泛使用的一个指标.通过这个指标,可以对图中节点的重要程度进行定量分析,可以衡量一个节点在网络通信中的重要性,识别出网络中的关键节点.较高的BC指标表明,一个节点到其它节点有相对较多的最短路径,或者这个节点位于其它两个节点最短路径上的可能性很大.BC反映了相应的节点在整个网络中的作用和影响力,是一个重要的全局几何量,具有很强的现实意义.例如,在社会关系网或技术网络中,介数的分布特征反映了不同人员、资源和技术在相应生产关系中的地位,这对于发现和保护关键资源、技术和人才具有重要意义.BC的计算是网络分析的重要内容,它占了大部分的计算时间.所以,对这个算法进行并行加速具有重要意义.
1 BC算法简介
节点v的BC为
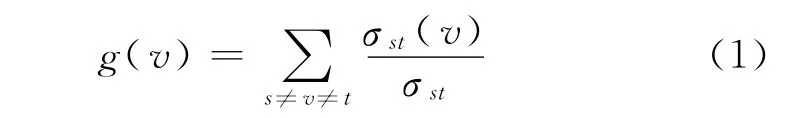
式中,σst为从节点s到节点t的最短路径总数目;σst(v)为这些路径中经过顶点v的路径条数.计算一个图中所有顶点的BC需要计算所有顶点间的最短路径,所需时间为O(n3).对于无权图,用Brandes算法计算所需时间为O(n×m)[3],其中,n为顶点的数目,m为边的数目.
Brandes算法由宽度优先搜索(breadth first search,BFS)、部分和累加、标准化等3个部分构成.对于图1所示的BC算法示例图中的b点,其BC值为
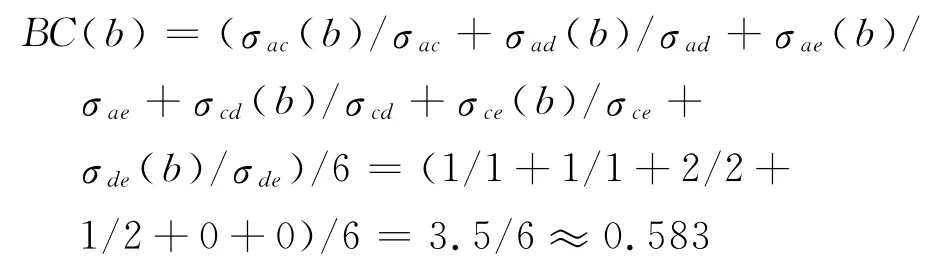
式中,σac(b)为经过b点从a到c的最短路径条数,σac为从a到c的最短路径条数.假定0除0等于0.为了使最终的BC位于[0,1]之间,还需要对结果进行标准化.所谓标准化对于无向图而言,就是除以(n-1)× (n-2)/2.对于有向图,就是除以(n-1)×(n-2).图1为无向图,n=5,(n-1)×(n-2)/2=6.
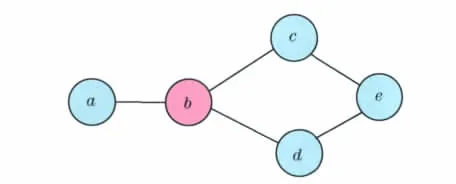
图1 BC算法示例图Fig.1 Example graph of BCalgorithm
2 并行BC算法
2.1 算法的数据结构
求解BC时,复杂网络的规模也是计算中必需面对的问题.在空间复杂度方面,目前复杂网络主要有邻接表和邻接矩阵两种表示方法.如果用邻接矩阵来表示复杂网络,其空间复杂度为V2,其中V是顶点的数目;对于节点数为1 000 000的复杂网络,计算机需要数T的内存才能表示,这对于目前的计算机几乎是不可能的.对于稀疏网络而言,用邻接表表示则占用较少的内存空间,因为它不需要存储不存在的边.如果使用数组来表示邻接表,对于无向图需要8E字节的存储容量,其中E是边的数目,每条边使用4字节,每一条边在邻接表中出现两次;而对于有向图,只需要4E字节的存储容量,因为每条边在邻接表中只出现一次.由于复杂网络往住是稀疏网络,因此,采用邻接表来存储网络.
本算法的开发语言为 Python 2.7[4],它是一种面向对象、直译式的计算机程序设计语言.其提供了Dict(字典)、Set(集合)、List(列表)及 Tuple(元组)等几种数据结构,其中,字典有时称为关联数组或者哈希表.它们通过键将一系列值联系起来,这样就可以使用键从字典中取出一项.本算法中采用字典来表示邻接表,将键值相同的值放在一个列表中,实现从键到值的多重映射.例如,对于以边表形式表示的图数据
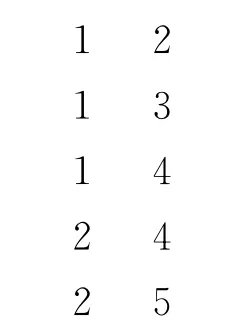
其对应的字典为{1:(2,3,4);2:(4,5)},顶点1和2为键,(2,3,4)及(4,5)分别为与键1和键2对应的值.由于Python对内存的使用非常节省,加上用整型的顶点编号来代替字符型的顶点名称,因此,对于325 729个顶点及1 497 134条边的网络[5],其内存占用不到200M.对于2 508 811个顶点及25 278 346条边的网络[6],其内存占用不到2G,因此,采用这种数据结构,能在目前流行的服务器上对上亿条边的复杂网络进行分析.
2.2 算法流程
本并行算法的开发环境为并行Python[7],它是一个Python模块,能够在SMP及工作站机群 上并行运行Python代码.BC的并行算法从每个源节点开始做宽度优先遍历,然后回溯累加得到BC.采用并行Python来实现粗粒度并行,将每个从源节点开始的遍历及回溯累加过程看作一个任务,算法需要n个任务,求得每个节点的部分BC值.最后,将每个任务的部分BC值累加,得到每个顶点的最终BC值,这n个任务可以并行处理,而且在并行计算过程中,各个节点间不需要通信,只需要一个并行规约操作得到最终的值.算法流程如图2所示.

图2 并行算法在管理节点及计算节点的执行流程Fig.2 Execution workflow of parallel algorithm in management and computation of nodes
在每个计算节点,都需要以源点s表示图的字典aDict,以及图的顶点集合G作为参数调用宽度优先遍历子程序,返回该源点对应的部分BC值,从该源点开始遍历时可以访问的顶点集合S,以及开始遍历时,节点v的前驱集合Pred,则对应的算法为


由于每个节点部分BC累加,规范化以及并行规约的算法比较简单,限于篇幅,这里不再表述.
2.3 性能评价
算法中,第15行用来从字典中查找顶点v是否存在于字典的键中,第16行用来在键中查找v,并返回与v对应的值,第17行用来判断w是否在字典D中,这3步是while循环中最耗时的部分.但由于Python字典采用哈希表实现,因此,能快速地检查一个键在字典中是否存在,查找效率可以达到O(1).需要指出的是,本算法只是实现了粗粒度的并行,因此并行效率不如考虑了图的邻接信息的中粒度及细粒度并行[8],但正因为不用考虑图的细节,因此实现起来相对简单,能够方便地应用到更多核心、更多工作站的机群.
3 实验结果
测试用的服务器包括一台用作管理节点的Dell PowerEdge R910工作站,它有32个至强L7555物理核心,128G内存,另有10台用作计算节点的Dell PowerEdge R810工作站,它们都有12个至强X5660物理核心,24G内存.测试的软件环境为CentOS5、intel icc编译器 11.1、Python2.7 以 及parallel python1.6.1,Python使用icc编译器编译以提高Python程序的执行速度.
本文测试了文献[5]的数据,它含有325 729个点,1 497 134条边.不同处理器数目k的所需计算时间t及加速比r如表1所示(见下页),相应的加速比曲线如图3所示(见下页).
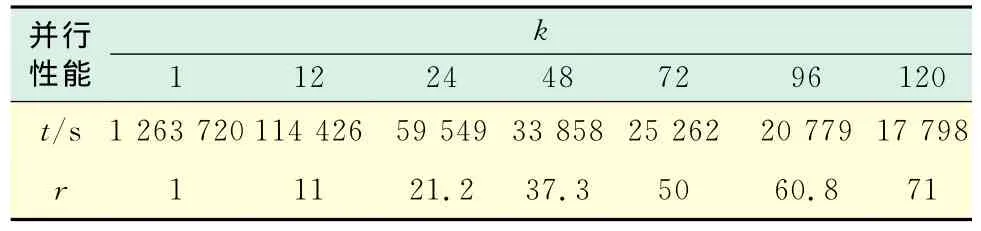
表1 处理器数目与计算时间及加速比对应关系表Tab.1 Relationship between number of processors,computing time and speedup
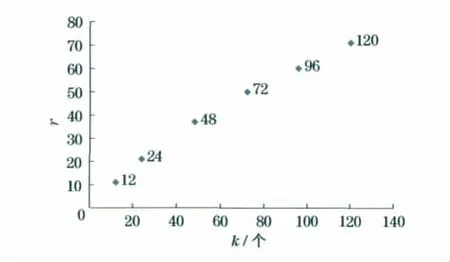
图3 加速比曲线Fig.3 Curve of speedup
从表1可以看出,串行算法计算BC需1 263 720s,约14d,如果在10台工作站共120个处理器中进行计算,所需时间只有17 798s,不到5h.从图3可以看出,随着处理器数目的增加,加速比也有线性上升的趋势.
4 结论及展望
在多核心工作站机群实现了计算介数的并行算法,为解决介数计算的时间与空间复杂度问题提供了易操作的方案,为分析更大规模复杂网络的特性打下了良好的基础.
未来的工作将探讨并行计算时的负载平衡问题,减少并行规约前的等待时间,提高计算速度.
[1]Wang X F,Chen G R.Complex networks:smallworld,scale-free and beyond [J].IEEE Circuits and Systems Magazine,2003,3(1):6-20.
[2]Freeman L C.A set of measures of centrality based on betweenness[J].Sociomtry,1977,40(1):35-41.
[3]Brandes U.A faster algorithm for betweenness centrality[J].Journal of Mathematical Socialogy,2001,25(2):163-177.
[4]Official website for pathon.python2.7.python[EB/OL].[2012-09-29].http:∥www.python.offical website for python.org/index.html.
[5]Albert R,Jeong H,Barabási A L.Internet:diameter of theworld wide web[J].Nature,1999,401(6749):130-131.
[6]苏磊,张宁,马良.一种新的大规模网络最短路径的近似算法[J].复杂系统与复杂性科学,2008,5(2):51-54.
[7]Offical website for parallel python.Parallel python1.6.1.parallel python[EB/OL].[2012-09-30].http:∥www.parallelpython.com/index.html.
[8]涂登彪,谭光明,孙凝晖.无锁同步的细粒度并行介度中心算法[J].软件学报,2011,22(5):986-995.
